大家可以先去看徐毅的《浅谈回文子串问题》。
马拉车算法是一个用来求最长回文子串的线性算法,由Manacher在1975年发明。
马拉车算法的代码复杂度较回文自动机低,对于一些问题已足够。回文自动机也有码量大,空间大,侧重于处理回文后缀等问题。
这就好比SA和SAM各有自己的优势,回文自动机和Manacher在处理回文串问题也有自己的侧重。
暴力求解最长回文子串的时间复杂度为O(n^2)O(n2),当然我们可以用字符串哈希+二分做到O(n×logn)。Manacher算法可以进一步优化到O(n)。
我们接下来就来看一看O(n)的做法。
因为回文串的长度可以为奇数,也可以为偶数。如xibobix和xiboobix。为了统一我们在每个字符两边插入一个不再字符集内的字符如‘#’,变为#x#i#b#o#b#i#x#,#x#i#b#o#o#b#i#x#。这样我们就不用分情况讨论了。
我们再引入一个新的与处理后的串等长的数组p,p_ipi?代表以ii为中心最长的回文半径。pi?=1代表只有s这一个字符。
如:
# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1
知道了pi有什么用呢?
看上面那个例子,以第二个 ‘1‘ 为中心的回文子串 "#2#2#1#2#2#" 的半径是6,而未添加#号的回文子串为 "22122",长度是5,为半径减1。
这是个巧合吗?
我们再看以第三个 ‘#‘ 为中心的回文子串 "#1#2#2#1#" 的半径是5,而未添加#号的回文子串为 "1221",长度是4,为半径减1。
总结一下:
```
定理1 以i为中心的回文串的长度为pi-1
```
证明:
(1) 先考虑以字符为中心的回文子串:
如"#2#2#1#2#2#",其形式必为"#c#c……# c #……c#c#",$其半径即为原串中的半径 \rimes 2$。因为这是奇回文串,$所以原串长度=原串半径 \times 2 − 1$。所以原串长度等于$pi?−1$.
(2) 以#为中心的回文子串:
首先在原串中这是个偶回文串。
其形式必为 "#c#c……#c # c#……c#c#",原串前一半的字符前都加一个#,长度为原串半径$\times 2$即为原串长度。而在后面添加一个#变为新串半径所以原串长度等于新串半径$−1$即$pi?−1$。
证毕
我们现在知道了长度却不知道具体的子串。所以我们还需要知道一个回文串在原串中的开始位置。
还是来看第二个$‘1‘$,它在处理后的串中排第$8$,半径为$6$,$8−6=2$,正是原串中的开始位置。
我们再来看第三个$‘#‘$,它在处理后的串中排第$5$,半径为$5$,$5−5=0$,这可不行。我们要把中心往后移一位才行,所以们要在一开始加一个不相干的字符(如‘@‘)。
之后再研(da)究(biao)一下发现了如下规律:
```
定理2 以i为中心的最长回文子串的开始位置为$\frac{i-p_i}{2}+1$
```
这个和定理1的证明及其相似,这里不再赘述。
接下来我们看怎么求出$p$数组。
我们可以先给$p$一个下界,再通过$s_{i-p}=s_{i+p}$来增加p。
我们需要新增两个变量$mx, id$,$mx$代表现在已匹配的回文串右端点最远能到达的位置的下一位,$id$代表$mx$的中心点,显然$mx=i+p[i]$。我们还需要利用已知的$p_k$。
接下来我们开始分类讨论。
(1)$i \geq mx$,这种情况我们对$[mx, i]$一无所知,只能把$p_i$设成$1$,再暴力匹配。
黑色部分是以id为中心的最长回文子串。

(2)$i < mx$,这种情况我们又得分两种情况讨论
我们找到$i$关于$id$的对称点,$id * 2 - i$,暂且记其为$j$。
mx-i>p_j ,如图
红色是以j为中心的回文串
绿色是红色的对称位置
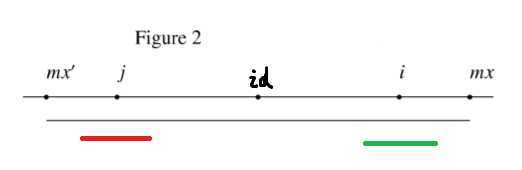
显然以$j$为中心的最长回文串到不了$mx‘$,这种情况我们不能确保$s_{i...mx}是否等于{s_{i-(mx-i)+1..i}}^r$,但我们可以肯定的是以$i$为中心的最长回文串的半径肯定不小于$p_j$。
由于回文所以红色部分一定等于绿色部分的翻转。有因为红色部分也是回文所以红色部分的翻转等于红色部分。
所以$p_i=p_j$。
$mx-i \leq p_j$,如图
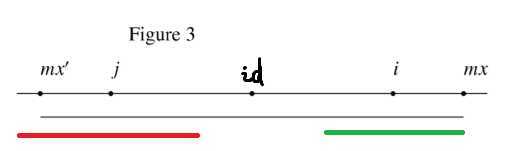
就比较遗憾,发现 $i+p_j-1 > mx$,这时我们的 $p_j$ 下界只能取到 $mx-i$。再暴力匹配
我们发现我们不会再mx以内在进行暴力匹配,所以暴力匹配是递增的,时间复杂度是$O(n)$。
模板题:
模板题,直接上代码。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 int n, n0, id, mx, res_len, res_center; 6 int p[50000000]; 7 char tmp[11100000], s[50000000]; 8 void Manacher() { 9 n0 = 0; 10 s[++n0] = ‘$‘; 11 for (int i = 1; i <= n; i++) s[++n0] = ‘#‘, s[++n0] = tmp[i]; 12 s[++n0] = ‘#‘; 13 id = mx = res_len = res_center = 0; 14 for (int i = 1; i <= n0; i++) { 15 p[i] = mx > i ? min(mx - i, p[id * 2 - i]) : 1; 16 while (s[i + p[i]] == s[i - p[i]]) ++p[i]; 17 if (mx < i + p[i]) mx = i + p[i], id = i; 18 if (res_len < p[i]) res_len = p[i], res_center = i; 19 } 20 } 21 int main() { 22 scanf("%s", tmp + 1); 23 n = strlen(tmp + 1); 24 Manacher(); 25 cout << res_len - 1; 26 return 0; 27 }
习题:
原文:https://www.cnblogs.com/zcr-blog/p/12400810.html