面试-仿射变换

面试题目

仿射变换,给出一个点在平面旋转$\theta$角的仿射矩阵.

题目内容

仿射变换(ATF,Affine Transformation) 是图像的线性变换,对于一个集合$X$ 的仿射变换可以表示为:
$$
f(x) = Ax+b, x \in X.
$$
对于我们需要处理的图像集合而言,可以表示为:
$$
g(x,y) = Af(x,y)+b.
$$
其中$A$矩阵就是仿射变换矩阵.

仿射变换

内容介绍可以参考链接:仿射变换介绍

常用的仿射变换包括:
缩放: Scale
旋转: Rotate
平移: Transform
反射: Reflection
错切: Shear

可以参考图:

仿射变换图示--wiki

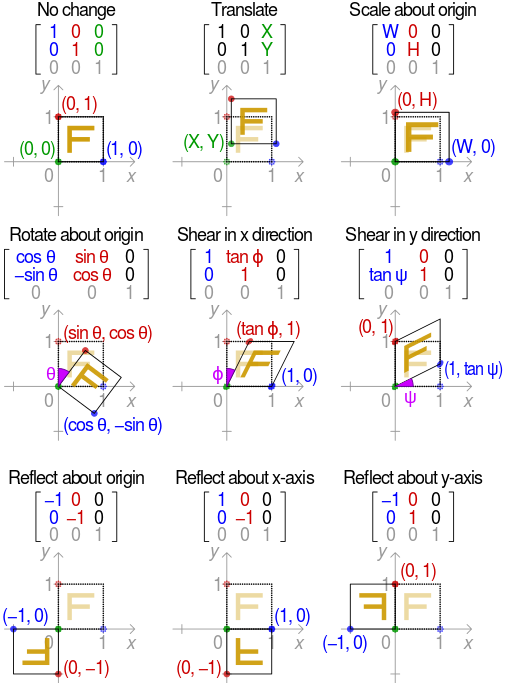
仿射变换中集合中的一些性质保持不变：
（1）凸性
（2）共线性：若几个点变换前在一条线上，则仿射变换后仍然在一条线上
（3）平行性：若两条线变换前平行，则变换后仍然平行
（4）共线比例不变性：变换前一条线上两条线段的比例，在变换后比例仍然步

注：所有的三角形都能通过仿射变化为其他三角形，所有平行四边形也能仿射变换为另一个平行四边形。

由于仿射变换是线性的,所以仿射变换的任意组合仍然是线性的.

仿射变换矩阵推导

仿射变换矩阵推导以 矩阵旋转为例,也是面试题目的内容:
假设原本点为 $C$ 点,旋转 $\theta$ 角度之后到达 $B$ 点, 计算旋转矩阵 A. 以二维矩阵为例

仿射变换旋转矩阵推导示意图

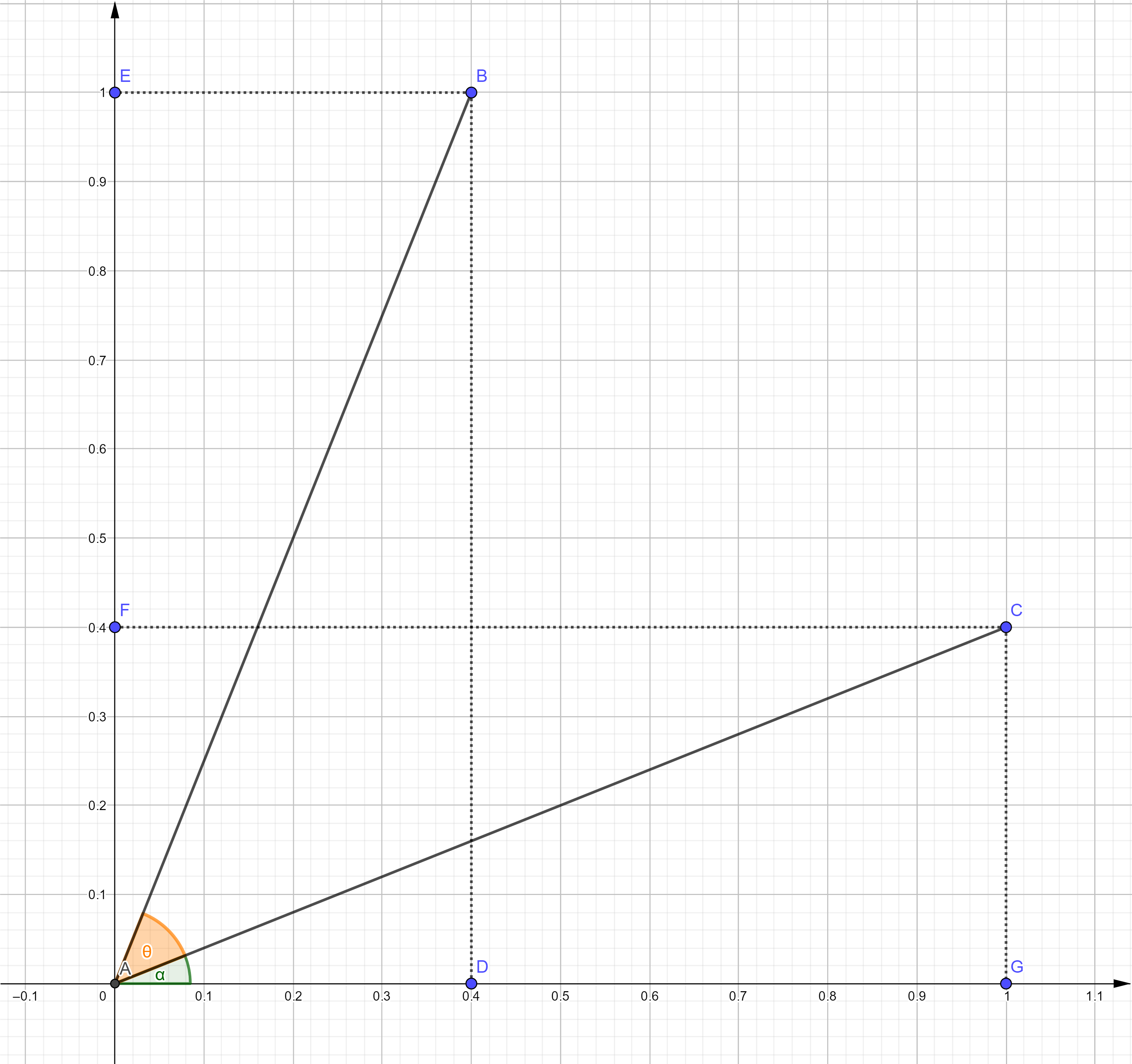
对于$C,B$两点表示成极坐标为 $C(r\cos\alpha,r\sin\alpha)$,$B(r\cos(\alpha+\theta),r\sin(\alpha+\theta))$,
对于
$$
x_B = r\cos(\alpha+\theta) = r(\cos\alpha\cos\theta-\sin\alpha\sin\theta) = (\cos\theta -\sin\theta)x_C
$$

$$
y_B = r\sin(\alpha+\theta) = r(\sin\alpha\cos\theta+\cos\alpha\sin\theta) = (\sin\theta+\cos\theta)y_C
$$
所以可以推导出如下矩阵
$$
\left[
\begin{array}{l}
{\mathrm{x_B}} \
{y_B}
\end{array}
\right]
=\left[
\begin{array}{cc}
{\cos \theta} & {-\sin \theta} \
{\sin \theta} & {\cos \theta}
\end{array}
\right]
\left[
\begin{array}{l}
{\mathrm{x_C}} \
{y_C}
\end{array}
\right]
$$

内容延展