$T$ 组测试数据。每次给你一个长度为 $n$ 的全排列 $p$,以及排列中第 $i$ 个数的颜色 $c_i$。每次操作会使 $p_i=p_{p_i} $,颜色不变。连续操作 $k$ 次,求最小的 $k$,使存在 $i$ 满足 $c_{i}=c_{p_i}=c_{p_{p_i}}= \cdots$
将排列映射为图,$i$ 向 $p_i$ 连边。显然,因为排列由若干个循环构成,所以这个图是若干个环。
一个点指向的点的编号就是它的 $p$ 的值。
考虑乘方操作的实质,$p^k$ 其实是 $i$ 指向的点按照环的方向顺移 $k-1$ 位。也就是,如果原来这个指针指向的是换上的第 $1$ 个数,那么现在指向的就是环上的第 $k$ 个数。
如图所示是将一个循环平方后的变化。
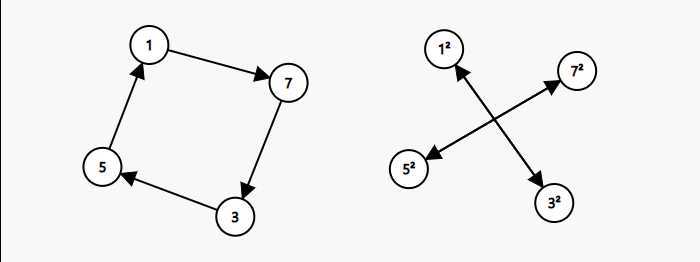
所以现在我们可以分别处理每一个环。
题目无非就是说,对一个环进行一种等距离遍历,使得路径上所有点的颜色相等。一个大小为 $s$ 的环的本质不同遍历方式只有 $d(s)$ 种,$d(s)$ 表示 $s$ 的因子个数,所以我们可以先枚举因数,再枚举起点,再遍历。
因数显然可以 $O(\sqrt{s})$ 处理出来,设当前因子为 $x$,那么枚举起点只需要枚举 $[0, x)$ 即可,而遍历一遍需要遍历 $\frac{s}{x}$ 个,所以时间复杂度是 $O(\sqrt{s} + s \cdot d(s))$。我的代码里对因子排了个序,其实是不必要的,只要确保都枚举就行。
判断方案的合法性无非就是路径上所有颜色拉出来看看是不是都相同。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n, p[N], c[N], ans;
bool vis[N];
vector<int> col, fact;
void GetFact()
{
fact.clear();
fact.push_back(1);
for(int i = 1; i * i <= col.size(); i++)
{
if(col.size() % i) continue;
fact.push_back(i);
if(i * i != col.size()) fact.push_back(col.size() / i);
}
sort(fact.begin(), fact.end());
}
void Solve()
{
GetFact();
for(int s : fact) for(int i = 0; i < s; i++)
{
bool ok = true;
for(int j = i; j < col.size(); j += s)
if(col[j] != col[i]) { ok = false; break; }
if(ok) { ans = min(ans, s); return; }
}
}
int main()
{
int T;
cin >> T;
while(T--)
{
cin >> n;
ans = n;
for(int i = 1; i <= n; i++) vis[i] = false;
for(int i = 1; i <= n; i++) cin >> p[i];
for(int i = 1; i <= n; i++) cin >> c[i];
for(int i = 1; i <= n; i++)
{
if(vis[i]) continue;
col.clear();
int j = i;
while(!vis[j]) col.push_back(c[j]), vis[j] = true, j = p[j];
Solve();
}
cout << ans << endl;
}
return 0;
}
Codeforces 1327D Infinite Path
原文:https://www.cnblogs.com/syksykCCC/p/CF1327D.html