图形学之信号处理

随着图形学学习深入，会遇到连续函数不能直接用于数字计算机，必须进行数字化处理的情况。处理连续函数最有效的方法之一，就是函数的采样值，将函数在多个不同点处的值存储起来，需要时就重构其他函数值。本节将概述采样与重构技术。

一、数字音频：一维采样

记录音频信号的数字方法是采样，模数转换器（ADC）每秒钟测量电压数千次，产生整数流。这些整数可以很容易的存储在媒体中。在播放录音时，按照适当的速度读出数据，然后送入数模转换器（DAC）中。

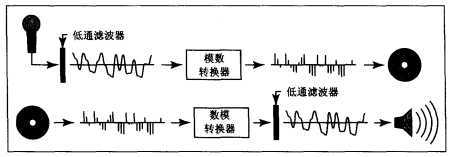
要使重构出的音频具有较高的质量，每秒的采样次数取决于所记录声音的音调高低。

采样干扰与走样

数字音频记录链可以作为图形学采样与重构过程的具体模型。在图形学的图像或者其他采样信号中，也会出现同样的欠采样干扰和重构干扰现象。
问题原因：采样频率太低。
解决办法：采样前滤波，重构过程中再次滤波。

二、卷积

卷积概念在采样与重构算法中广泛被应用，它是一个简单的数学概念，是采样、滤波、重构等算法的基础。
卷积是函数的运算，有两个函数产生一个新的函数。卷积可用于连续函数和离散序列；可用于一维、二维活高维定义域的函数（维度是按自变量个数计算得来）。

（一）滑动平均

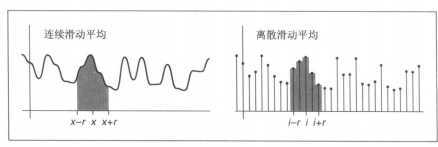
举例：采用滑动平均对一位韩束进行平滑处理。
为了获得任意点的平滑值，计算该店 \(r\) 邻域的函数平均值（\(r\) 是指平滑运算的半径，是一个控制平滑程度的参数）。

计算：

1. 连续函数 \(g(x)\) —— 在某个区间上对 \(g\) 积分，然后除以区间长度2r：

2. 离散函数 \(b[i]\) —— 平均就是将索引范围内（ \(2r+1\) ）累加求平均：

卷积的本质是滑动平均思想，唯一的区别是卷积中的滑动平均是加权平均。

（二）离散卷积

离散卷积计算：
对离散序列 \(a[i]\)、\(b[i]\)进行卷积，结果为离散序列 \((a * b)[i]\)，该过程类似爱用序列 \(a\) 所给的样本赋予加权值，对 b 进行滑动平均。
例：索引为 \(i-j\) 的样本 \(b[i-j]\)的权重为 \(a[j]\)。这是 \(a\) 卷积 \(b\) （\(a*b\)）的计算公式表示：

上式是对所有整数的求和运算（\(- \infty \rightarrow + \infty\)）

在图形学中，一般两个函数中由一个具有有限支撑集（意味着旨在自变量的有限区域内取非零值）。假设 \(a\) 有限，存在半径为 \(r\) ，使得当\(|j|>r\)时，都有 \(a[j]=0\),上面的求和公式再完整为：

(三)

图形学之信号处理

原文：https://www.cnblogs.com/somedayLi/p/12571350.html