本质上用区间去解决区间问题,而非点去解决区间问题,从而简化时间复杂度。
| 操作 | 复杂度 |
|---|---|
| 点查询修改 | log(n) |
| 区间查询修改 | log(n) |
lazy操作原理:把该深入的区间深入,包含的区间直接打上标记。
| 操作集 | 原理 | 复杂度 |
|---|---|---|
| push_up | 把点root的左右add更新,统计到当前root | log(n) |
| push_down | 把点root的左右节点向下扩展,打上标记 | log(n) |
| update | 更新区间,先push_down,再update左右,再push_up | log(n) |
| query | 查询区间,先push_down,再向下查询 | log(n) |
二:树状数组
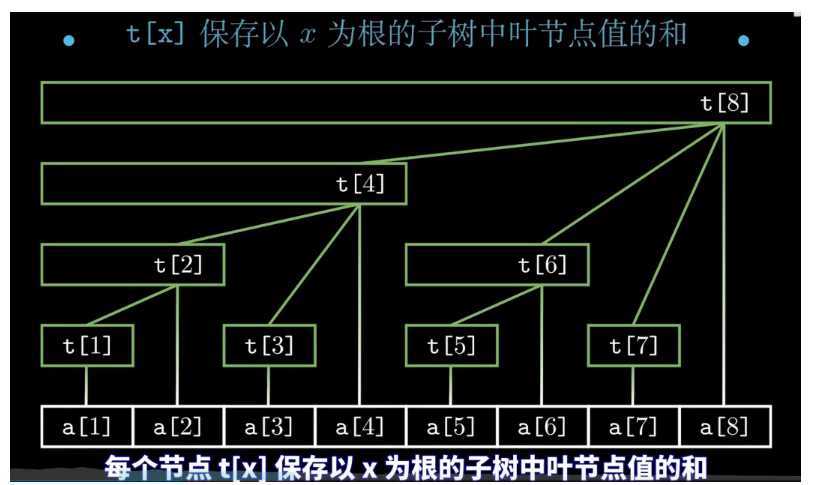
树状数组就是这样一个奇妙的数据结构(动态维护前缀和)
做出他每个节点的的lowbit:
观察后有以下规律:
t[x]保存以x为根节点的子树节点的值和
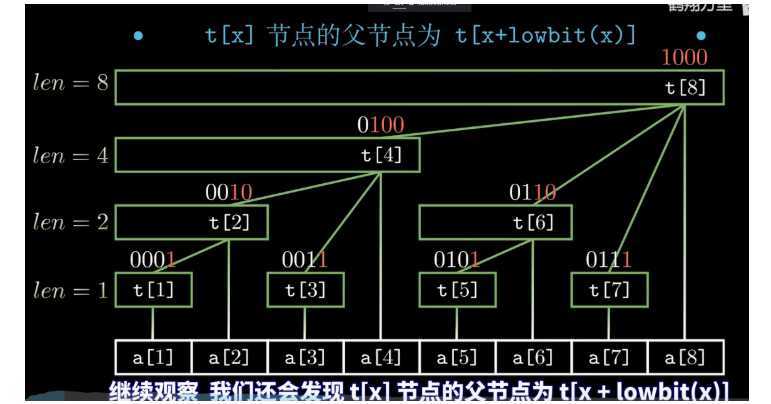
1.这个节点x 的层数即为 lowbitx
2.节点x,覆盖的区间长度即可lowbitx
3.一个节点加上它的lowbit之后,就变成了它的祖先父节点
可得如下公式:
| 操作 | 最坏复杂度 | 做法 |
|---|---|---|
| 点修改 | log(n) | 找到节点,然后一直 +lowbit(x),到父结点,动态维护区间和 |
| 区间查询 | log(n) | 找到节点,然后一直 -lowbit(x),到子结点,跳着查询区间和,然后前缀和相减 |
点修改:
区间查询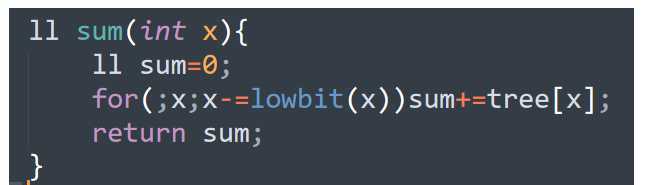
原文:https://www.cnblogs.com/littlerita/p/12576639.html