主要是想存个树状数组的板子顺便orz一下dyls
在解题过程中,我们有时需要维护一个数组的前缀和S[i]=A[i]+A[2]+...+A[i]。但是不难发现,如果我们修改了任意一个A[i],S[i],S[i+1]...S[n]都会发生变化。可以说,每次修改A[i]后,调整前缀和S在最坏的情况下会需要O(n)的时间。当n非常大时,就GG啦。树状数组的修改与求和都是O(logn),效率较高。(但是对于dyls来说就非常非常慢啦,一般来说dyls会使用O(1)的dy算法 )
)
根据任意正整数关于2的不重复次幂的唯一分解性质,若一个正整数x的二进制表示为10101,其中等于1的位是0,2,4,则正整数x可以被“二进制分解”成24+22+20。进一步地,区间[1,x]可以分成O(logx)个小区间:
1.长度为24的小区间[1,24]
2.长度为22的小区间[24+1,24+22]
3.长度为20的小区间[24+24+1,24+22+20]
对于区间 [1,x],树状数组将其分为 logx 个子区间,从而满足快速询问区间和。
这些子区间的共同特点是:若区间结尾为R,则区间长度就等于R的“二进制分解”下最小的2的次幂,我们设为 lowbit(R)。对于给定的序列a,我们建立一个数组 f,其中f[x]保存序列a的区间[x-lowbit(x)+1,x]中所有数的和。
(摘自《信息学奥赛一本通》)
lowbit(x)表示取出非负整数x在二进制表示下最低位的1以及它后边的0构成的数值。
如何得出 lowbit(x)=x&(-x)?
设x>0,x的第k为是1,第0~k-1位都是0。
为了实现 lowbit 运算,先把x取反,此时第k位变为0,第0~k-1位都是1。再令 x=x+1,此时因为进位,第k为变为1,第0~k-1位都是0。在上面的取反加1操作后,x的第k+1到最高位恰好与原来相反,所以 x&(~x+1) 仅有k位为1,其余位都是0。而在补码表示下,~x=-1-x,因此 lowbit(x)=x(~x+1)=x&(-x)。

即给序列中的某个数 a[x]加上y。只有结点 f[x] 及其所有祖先结点保存的“区间和”包含a[x],而任意一个结点的祖先至多只有logN个,我们逐一对它们的数组f值进行更新即可。(莫名压行)

即求序列a第1~写个数的和。我们可以求出x的二进制表示中每个等于1的位,把[1,x]分成 O(logN) 个小区间,而每个小区间的区间和都已经保存在数组f中。

如果要查询序列a的区间 [l,r] 中所有数的和,只需计算 get(r)-get(l-1)。
一维树状数组的每个操作的复杂度都是O(logn)的。塔可以扩充为m维,这样每个操作的复杂度就变成了O(logmn),在m不大的时候,时间复杂度是可以接受的。扩充的方法就是将原来的修改和查询函数中的一个循环,改成m个循环m维数组f中的操作。就是说,如果有n×m的二维数组a,树状数组为f,那么可以如下操作(只有二维树状数组的板子):
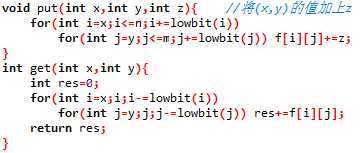
要注意树状数组能处理的是下标为1...n的数组,不能出现下标为0的情况。因为 lowbit(0)=0,会陷入死循环然后GG。
这是一道模板题。
给定数列a[1],a[2],...,a[n],你需要依次进行q个操作,操作有两类:
1 i x:给定 i,x,将 a[i] 加上x;
2 l r:给定 l,r,求 的值$\sum_{i=l}^r{a[i]}$(换言之,求 a[l]+a[l+1]+...+a[r] 的值)。
here 按照上述做法写就阔以AC啦。
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=1e6+5; 6 int n,q,f[N],opt,x,y; 7 void put(int x,int y){ 8 for(;x<=n;x+=lowbit(x)) f[x]+=y; 9 } 10 int get(int x){ 11 int res=0; 12 for(;x;x-=lowbit(x)) res+=f[x]; 13 return res; 14 } 15 signed main(){ 16 //freopen(".in","r",stdin); 17 //freopen(".out","w",stdout); 18 scanf("%lld%lld",&n,&q); 19 for(int i=1;i<=n;i++) 20 scanf("%lld",&x),put(i,x); 21 while(q--){ 22 scanf("%lld%lld%lld",&opt,&x,&y); 23 if(opt==1) put(x,y); 24 else printf("%lld\n",get(y)-get(x-1)); 25 } 26 return 0; 27 }
这是一道模板题。
给定数列a[1],a[2],...,a[n],你需要依次进行q个操作,操作有两类:
1 l r x:给定 l,r,x,对于所有 i∈[l,r],将a[i]加上x(换言之,将 a[l]+a[l+1]+...+a[r] 分别加上x)
2 i:给定i,求a[i]的值。
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=1e6+5; 6 int n,q,f[N],opt,x,y,k; 7 void put(int x,int y){ 8 for(;x<=n;x+=lowbit(x)) f[x]+=y; 9 } 10 int get(int x){ 11 int res=0; 12 for(;x;x-=lowbit(x)) res+=f[x]; 13 return res; 14 } 15 signed main(){ 16 //freopen(".in","r",stdin); 17 //freopen(".out","w",stdout); 18 scanf("%lld%lld",&n,&q); 19 for(int i=1;i<=n;i++) 20 scanf("%lld",&x),put(i,x-y),y=x; 21 while(q--){ 22 scanf("%lld",&opt); 23 if(opt==1) scanf("%lld%lld%lld",&x,&y,&k),put(x,k),put(y+1,-k); 24 else scanf("%lld",&x),printf("%lld\n",get(x)); 25 } 26 return 0; 27 }
这是一道模板题。
给定数列a[1],a[2],...,a[n],你需要依次进行q个操作,操作有两类:
1 l r x:给定 l,r,x,对于所有 i∈[l,r],将a[i]加上x(换言之,将 a[l]+a[l+1]+...+a[r] 分别加上x)
2 l r:给定 l,r,求 的值$\sum_{i=l}^r{a[i]}$(换言之,求 a[l]+a[l+1]+...+a[r] 的值)。
建立两个树状数组f0,f1,起初全部赋值为零。对于每条指令“1 l r x”,执行4个操作:
1.在树状数组f0中,把位置l上的数加x。
2.在树状数组f0中,把位置r+1上的数减x。
3.在树状数组f1中,把位置l上的数加l*x。
4.在树状数组f1中,把位置r+1上的数减(r+1)*x。
另外,我们建立数组sum存储序列a的原始前缀和。对于每条指令“2 l r”,拆分成 1~r 和 1~l-1两部分,二者相减。写成式子就是:
$(sum[r]+(r+1)*get(f_0,r)-get(f_1,r))-(sum[l-1]+l*get(f_0,l-1)-get(f_1,l-1))$
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=1e6+5; 6 int n,q,f[2][N],sum[N],opt,l,r,x,ans; 7 void put(int k,int x,int y){ 8 for(;x<=n;x+=lowbit(x)) f[k][x]+=y; 9 } 10 int get(int k,int x){ 11 int res=0; 12 for(;x;x-=lowbit(x)) res+=f[k][x]; 13 return res; 14 } 15 signed main(){ 16 //freopen(".in","r",stdin); 17 //freopen(".out","w",stdout); 18 scanf("%lld%lld",&n,&q); 19 for(int i=1;i<=n;i++) 20 scanf("%lld",&x),sum[i]=sum[i-1]+x; 21 while(q--){ 22 scanf("%lld%lld%lld",&opt,&l,&r); 23 if(opt==1) scanf("%lld",&x),put(0,l,x),put(0,r+1,-x),put(1,l,l*x),put(1,r+1,-(r+1)*x); 24 else{ 25 ans=sum[r]+(r+1)*get(0,r)-get(1,r); 26 ans-=sum[l-1]+l*get(0,l-1)-get(1,l-1); 27 printf("%lld\n",ans); 28 } 29 } 30 return 0; 31 }
给出一个n×m的零矩阵A,你需要完成如下操作:
1 x y k:表示元素 Ax,y 自增k;
2 a b c d:表示询问左上角为(a,b),右下角为(c,d)的子矩阵内所有数的和。
here 按照之前的做法写就ok啦。
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=(1<<12)+5; 6 int n,m,opt,a,b,c,d,k,f[N][N]; 7 void put(int x,int y,int z){ 8 for(int i=x;i<=n;i+=lowbit(i)) 9 for(int j=y;j<=m;j+=lowbit(j)) f[i][j]+=z; 10 } 11 int get(int x,int y){ 12 int res=0; 13 for(int i=x;i;i-=lowbit(i)) 14 for(int j=y;j;j-=lowbit(j)) res+=f[i][j]; 15 return res; 16 } 17 signed main(){ 18 //freopen(".in","r",stdin); 19 //freopen(".out","w",stdout); 20 scanf("%lld%lld",&n,&m); 21 while(~scanf("%lld",&opt)){ 22 if(opt==1){ 23 scanf("%lld%lld%lld",&a,&b,&k); 24 put(a,b,k); 25 } 26 else{ 27 scanf("%lld%lld%lld%lld",&a,&b,&c,&d); 28 printf("%lld\n",get(c,d)-get(a-1,d)-get(c,b-1)+get(a-1,b-1)); 29 } 30 } 31 return 0; 32 }
给出一个n×m的零矩阵A,你需要完成如下操作:
1 a b c d k:表示左上角为(a,b),右下角为(c,d)的子矩阵内所有数都自增k;
2 x y:表示询问元素 Ax,y 的值。
here 二维树状数组区间修改和一维树状数组区间修改的原理是一样的,按照这个做法写一下就AC啦。
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=(1<<12)+5; 6 int n,m,opt,a,b,c,d,k,f[N][N]; 7 void put(int x,int y,int z){ 8 for(int i=x;i<=n;i+=lowbit(i)) 9 for(int j=y;j<=m;j+=lowbit(j)) f[i][j]+=z; 10 } 11 int get(int x,int y){ 12 int res=0; 13 for(int i=x;i;i-=lowbit(i)) 14 for(int j=y;j;j-=lowbit(j)) res+=f[i][j]; 15 return res; 16 } 17 signed main(){ 18 //freopen(".in","r",stdin); 19 //freopen(".out","w",stdout); 20 scanf("%lld%lld",&n,&m); 21 while(~scanf("%lld",&opt)){ 22 if(opt==1){ 23 scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k); 24 put(a,b,k),put(a,d+1,-k),put(c+1,b,-k),put(c+1,d+1,k); 25 } 26 else{ 27 scanf("%lld%lld",&a,&b); 28 printf("%lld\n",get(a,b)); 29 } 30 } 31 return 0; 32 }
给出一个n×m的零矩阵,直到输入文件结束,你需要进行若干个操作,操作有两类:
1 a b c d x:表示左上角为(a,b),右下角为(c,d)的子矩阵内全部加上x;
2 a b c d:表示询问左上角为(a,b),右下角为(c,d)为顶点的子矩阵的所有数字之和。
1 #include<bits/stdc++.h> 2 #define lowbit(x) x&(-x) 3 #define int long long 4 using namespace std; 5 const int N=2100; 6 int n,m,opt,a,b,c,d,k; 7 struct data{ 8 int f[N][N]; 9 void put(int x,int y,int z){ 10 for(int i=x;i<=n;i+=lowbit(i)) 11 for(int j=y;j<=m;j+=lowbit(j)) f[i][j]+=z; 12 } 13 int get(int x,int y){ 14 int res=0; 15 for(int i=x;i;i-=lowbit(i)) 16 for(int j=y;j;j-=lowbit(j)) res+=f[i][j]; 17 return res; 18 } 19 }v1,v2,v3,v4; 20 void put2(int x,int y,int k){ 21 v1.put(x,y,k); 22 v2.put(x,y,(y-1)*k); 23 v3.put(x,y,(x-1)*k); 24 v4.put(x,y,(x-1)*(y-1)*k); 25 } 26 int get2(int x,int y){ 27 return x*y*v1.get(x,y)-x*v2.get(x,y)-y*v3.get(x,y)+v4.get(x,y); 28 } 29 signed main(){ 30 //freopen(".in","r",stdin); 31 //freopen(".out","w",stdout); 32 scanf("%lld%lld",&n,&m); 33 while(~scanf("%lld",&opt)){ 34 if(opt==1){ 35 scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k); 36 put2(a,b,k),put2(a,d+1,-k),put2(c+1,b,-k),put2(c+1,d+1,k); 37 } 38 else{ 39 scanf("%lld%lld%lld%lld",&a,&b,&c,&d); 40 printf("%lld\n",get2(c,d)-get2(a-1,d)-get2(c,b-1)+get2(a-1,b-1)); 41 } 42 } 43 return 0; 44 }
原文:https://www.cnblogs.com/maoyiting/p/12561756.html