一.信息的用处?

信息的作用:对不确定性的消除。
由于信息是来判断事请的不确定性,一件事的不确定信息越大,所提供的信息越多,
例如一件事发生的概率为1,它能提供的信息量为0;但是如果一件事发生的概率为趋近于0,但是它发生了,它表示的信息量就很巨大了!
为了表达一件事情所包含的信息量,人们提出了自信息的概念。
二.自信息(用于衡量随机事件所包含的信息量有多少)

(一)自信息的公式:

自信息用来描述一件事请发生所产生的信息量的大小,比如一件事请发生概率为1,那么P(a)=1,
所以I(a)=log(1/P(a))=0(log的底数一般要大于1,就是说这个函数一定要是单调递增函数,一般取2为底),表示产生的信息量为0。
而如果一件事请发生的概率很小,例如P(a)=0.01,那么I(a)=log(1/P(a))=log(100),那么这个信息量就比较巨大了!
(二)对于公式I(a)=log(1/p(a))底数的取值
(1) 你可以取log的底数在(0,1)之间.
这时候如果事情发生的概率P(a)越大,说明它信息量越小。根据公式有P(a)越大,那么1/P(a)就越小,那么I(a)=log(1/P(a))就越大,
此时你可以把这个公式理解为,值越大,提供的信息越少。
(2)你可以取log的底数在大于1.
则一般底数取2,看起来更直观,此时如果一件事发生的概率P(a)越大,说明它信息量越小。根据公式有P(a)越大,那么1/P(a)就越小,那么I(a)=log(1/P(a))就越小,
此时你可以把这个公式理解为,值越小,提供的信息越少(这样用公式结果的大小来表示信息大小更直观,不是吗?)。
(三)自信息的图像
log图像

注意:由于一件事请发生的概率大小在[0,1]之间取值,所以当a>1时,log(1/P(a))取值范围是[1,+无穷),当然当(0<a<1)时,log(1/P(a))取值范围也是[1,+无穷).
所以当a>1时,取值范围为蓝色区域,当0<a<1时取值范围为红色区域
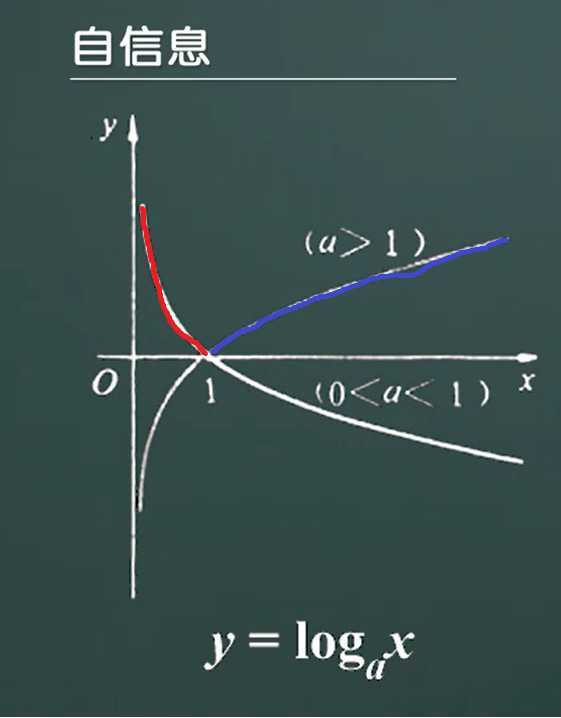
三.如何衡量一个随机系统的信息量大小
(1)随机系统是啥?
我不想说的那么学术化,这里的随机系统说白了就是一个集合,假设这个集合只包含数字,那么在这个集合里面所表示的数字可能千变万化,这个千变万化的数字取值,就是一个随机系统。
再打个比方,我们在随机选一个时间段,然后随机在地球上取一片森林,那么这片森林就可以看作一个随机系统。
那么我们吃饱没事干,定义一个随机系统的概念干什么呢?
因为我们有时候要研究某个随机系统的总信息量有多少,拿上面的那片森林打比方,假设这片森林了的东西都是随机变化的。
此时我们提出一个问题:例如我们要研究这片森林的变化是怎样的?有多少种草本植物
有多少鸟类,有多少种虫子……
那么我们应该如何衡量这个随机系统的信息量的大小呢?
此时聪明的先人提出了信息熵的概念!
(2)信息熵
信息熵——定义信息的度量。

看上面的定义,大白话理解就是,取每一件事情的自信息进行相加,然后取平均值,so easy!
信息熵公式:
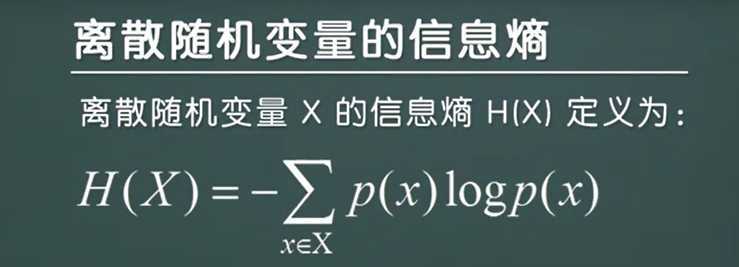
注:公式理解-->H(X)表示信息熵的值,H(X)=每一个随机随机事件的变量的概率乘上它相对应的信息熵。(-?,主要是因为log(1/P(X))变成log(P(X))提取出来的符号 )
你可能有疑问,为什么要多乘上一个P(X),直接取每一件事的信息熵相加求和不是很好吗,干嘛多此一举,让公式复杂化!
答案就是:你考虑过log(0)吗,它是一个无穷大的值,要是有它存在,那么就乱套了,所以加上P(X),见下面。

原文:https://www.cnblogs.com/hmy-666/p/12581131.html