《Explaining and harnessing adversarial examples》
论文学习报告
组员:裴建新 赖妍菱 周子玉
2020-03-27
Szegedy有一个有趣的发现:有几种机器学习模型,包括最先进的神经网络,很容易遇到对抗性的例子。所谓的对抗性样例就是对数据集中的数据添加一个很小的扰动而形成的输入。在许多情况下,在训练数据的不同子集上训练不同体系结构的各种各样的模型错误地分类了相同的对抗性示例。这表明,对抗性例子暴露了我们训练算法中的基本盲点。
对抗性例子是如何产生的?
论文中提到对抗性例子是由于深度神经网络的极端非线性与模型平均不足和纯监督学习问题的正则化不足相共同导致的。在高维空间中,线性行为很容易引起对抗性的例子。这使我们能够设计一种快速生成对抗性示例的方法,从而使对抗性训练变得实用,而对抗性训练也可以带来额外的正则化收益。一般的正则化策略并不能显著降低模型对对抗例子的脆弱性,但像RBF网络这样的非线性模型族转变可以做到这一点。通过论文,我们可以发现在设计易于训练的模型(由于其线性)和设计使用非线性效应来抵抗对抗性扰动的模型之间存在一种基本的张力。从长远来看,通过设计更强大的优化方法来成功地训练更多的非线性模型,可以避免这种情况。
Szegedy演示了神经网络和相关模型的各种有趣特性。与论文最相关的包括:
1)边界约束的L-BFGS(限域拟牛顿法)可以可靠地找到对抗性的例子。
2)在一些数据集上,比如ImageNet (Deng等人,2009年),对抗性的例子与原始的例子非常接近,以至于人眼无法区分它们之间的差异。
3)具有不同体系结构的各种分类器或在训练数据的不同子集上训练的各种分类器常常会对同一个对抗性示例进行错误分类。
4)浅层的softmax回归模型也容易受到对抗性例子的影响
5)对反例的训练可以使模型规范化——但是,由于需要在内部循环中进行代价高昂的约束优化,这在当时并不实际。
这些结果表明,基于现代机器学习技术的分类器,即使是那些在测试集上获得优异性能的分类器,也没有学习决定正确输出标签的真正基本概念。相反,这些算法构建了一个在自然发生的数据上运行良好的“波将金村”,但当人们访问数据分布中不具有高概率的空间点时,它就暴露为一个假货。这尤其令人失望,因为在计算机视觉中流行的一种方法是使用卷积网络特性作为欧氏距离近似感知距离的空间。如果感知距离非常小的图像对应于网络中完全不同的类,那么这种相似性显然是有缺陷的。
Softmax是用于分类过程,实现多分类,简单来说,它把一些输出的神经元映射到(0-1)之间的实数,并且归一化保证和为1,从而使得多分类的概率之和也刚好为1。这是一种较为通俗的解释,当然我们也可以直接从这个名字入手去解释,Softmax可以分为soft和max,max也就是最大值,假设有两个变量a,b。如果a>b,则max为a,反之为b。那么在分类问题里面,如果只有max,输出的分类结果只有a或者b,是个非黑即白的结果。但是在现实情况下,我们希望输出的是取到某个分类的概率,或者说,我们希望分值大的那一项被经常取到,而分值较小的那一项也有一定的概率偶尔被取到,所以我们就应用到了soft的概念,即最后的输出是每个分类被取到的概率。
Softmax函数定义如下:
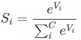
其中,Vi 是分类器前级输出单元的输出。i 表示类别索引,总的类别个数为 C。Si 表示的是当前元素的指数与所有元素指数和的比值。(划重点)通过这个Softmax函数 就可以将多分类的输出数值转化为相对概率。
下面通过这个图片可以更直观展示:
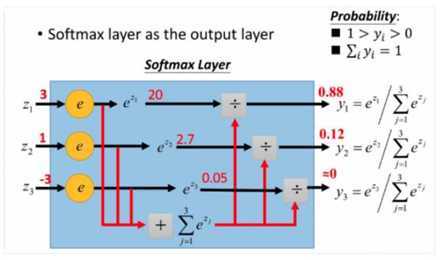
首先后面一层作为预测分类的输出节点,每一个节点就代表一个分类,如图所示,那么这7个节点就代表着7个分类的模型,其中i就是节点的下标次序。最有趣的是最后一层有这样的特性:
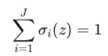
也就是说最后一层的每个节点的输出值的加和是1。这种激励函数从物理意义上可以解释为一个样本通过网络进行分类的时候在每个节点上输出的值都是小于等于1的,是它从属于这个分类的概率。
1985年,Powell提出了多变量插值的径向基函数(RBF)方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。最常用的径向基函数是高斯核函数,其一般形式为k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
RBF神经网络是一种三层神经网络,其包括输入层、隐层、输出层。从输入空间到隐层空间的变换是非线性的,而从隐层空间到输出层空间变换是线性的。流图如下:
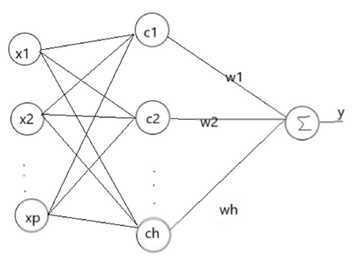
RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和,此处的权即为网络可调参数。其中,隐含层的作用是把向量从低维度的p映射到高维度的h,这样低维度线性不可分的情况到高维度就可以变得线性可分了,主要就是核函数的思想。这样,网络由输入到输出的映射是非线性的,而网络输出对可调参数而言却又是线性的。网络的权就可由线性方程组直接解出,从而大大加快学习速度并避免局部极小问题。
径向基神经网络的激活函数可表示为:
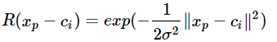
其中xp径向基神经网络的结构可得到网络的输出为:
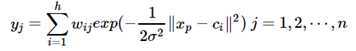
当然,采用最小二乘的损失函数表示:
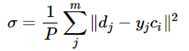
简单概括就是如下流程:
1、输入层到隐藏层之间不是通过权值和阈值进行连接的,而是通过输入样本与隐藏层点之间的距离(与中心点的距离)连接的。
2、得到距离之后,将距离代入径向基函数,得到一个数值。数值再与后边的权值相乘再求总和,就得到了相应输入的输出。
3、在训练网络之前,需要确定中心点的个数,和中心点的位置。以及求出隐藏层各径向基函数的方差(宽窄程度)。和隐藏层和输出层之间的权值。
4、中心点个数、中心点位置、方差、权值都可以通过下文所述的方法求出来。
5、径向基函数也是一种基,可以通过对其线性组合,来对非线性函数进行拟合。
6、RBF神经网络只需要了解其中的原理。然后给了训练数据,求出上述几个参数,再输入测试数据,就可以预测输出了。
Maxout是深度学习网络中的一层网络,就像池化层、卷积层一样等,我们可以把maxout 看成是网络的激活函数层。我们假设网络某一层的输入特征向量为:X=(x1,x2,……xd),也就是我们输入是d个神经元。Maxout隐藏层每个神经元的计算公式如下:
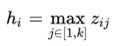
上面的公式就是maxout隐藏层神经元i的计算公式。其中,k就是maxout层所需要的参数了,由我们人为设定大小。就像dropout一样,也有自己的参数p(每个神经元dropout概率),maxout的参数是k。公式中Z的计算公式为: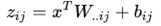 ,权重w是一个大小为(d,m,k)三维矩阵,b是一个大小为(m,k)的二维矩阵,这两个就是我们需要学习的参数。如果我们设定参数k=1,那么这个时候,网络就类似于以前我们所学普通的MLP网络。
,权重w是一个大小为(d,m,k)三维矩阵,b是一个大小为(m,k)的二维矩阵,这两个就是我们需要学习的参数。如果我们设定参数k=1,那么这个时候,网络就类似于以前我们所学普通的MLP网络。
我们可以这么理解,本来传统的MLP算法在第i层到第i+1层,参数只有一组,然而现在我们不怎么干了,我们在这一层同时训练n组参数,然后选择激活值最大的作为下一层神经元的激活值。下面还是用一个例子进行讲解,比较容易搞懂。
(1)以前MLP的方法。我们要计算第i+1层,那个神经元的激活值的时候,传统的MLP计算公式就是:
z=W*X+b
1. Maxout 的方法。如果我们设置maxout的参数k=5,maxout层就如下所示:
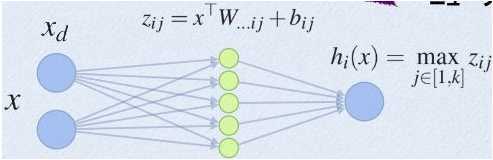
相当于在每个输出神经元前面又多了一层。这一层有5个神经元,此时maxout网络的输出计算公式为:
z1=w1*x+b1
z2=w2*x+b2
z3=w3*x+b3
z4=w4*x+b4
z5=w5*x+b5
out=max(z1,z2,z3,z4,z5)
3.4 对抗性例子产生的原因
在许多问题中,单个输入特性的精度是有限的。例如,数字图像通常每像素只使用8bit,因此它们会丢弃动态范围内小于1/255的所有信息。由于特征的精度是有限的,如果每个元素的扰动 η 都小于特征的精度,分类器对输入x的响应不同于对抗性输入![]() 是不合理的。在形式上,对于类之间分离良好的问题,我们希望分类器将相同的类分配给x和
是不合理的。在形式上,对于类之间分离良好的问题,我们希望分类器将相同的类分配给x和![]() ,只要
,只要![]() ,其中
,其中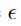 足够小,可以被与我们的问题相关的传感器或数据存储设备丢弃。
足够小,可以被与我们的问题相关的传感器或数据存储设备丢弃。
考虑一个权向量w和一个对抗性例子![]() 之间的点积:
之间的点积:
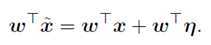
对抗性扰动使激活增加了![]() 。通过赋值
。通过赋值![]() ,我们可以在满足 η 的最大范数约束的情况下使这个增量最大化。如果w有n维,并且权向量中一个元素的平均大小为m,那么激活度将增加
,我们可以在满足 η 的最大范数约束的情况下使这个增量最大化。如果w有n维,并且权向量中一个元素的平均大小为m,那么激活度将增加![]() 。因为
。因为![]() 不随问题的维数增长,但激活的变化引起的扰动 η 可以伴随维度n线性增长,那么对于高维问题,我们可以对输入做许多无穷小的变化,来使输出产生一个巨大的改变。我们可以把这看作是一种“偶然的隐写术”,在这种情况下,一个线性模型被迫只关注与它的权值最接近的信号,即使存在多个信号,而其他信号的振幅要大得多。
不随问题的维数增长,但激活的变化引起的扰动 η 可以伴随维度n线性增长,那么对于高维问题,我们可以对输入做许多无穷小的变化,来使输出产生一个巨大的改变。我们可以把这看作是一种“偶然的隐写术”,在这种情况下,一个线性模型被迫只关注与它的权值最接近的信号,即使存在多个信号,而其他信号的振幅要大得多。
这个解释表明,一个简单的线性模型,如果它的输入具有足够的维数,可以有对抗性的例子。以前对对抗性例子的解释援引了神经网络的假设性质,比如假定的高非线性性质。我们基于线性的假设更简单,也可以解释为什么softmax回归容易遇到对抗性的例子。
对抗样本的线性视图提供了一种快速生成它们的方法,这意味着扰动在线性状态下更容易成功干扰模型判断结果。
这部分内容提出了快速梯度符号法(FGSM)来生成对抗样本。设 θ为模型的参数,x为模型的输入,y为与x相关的目标(有目标的机器学习任务),J(θ,x,y)为训练神经网络的成本函数。我们可以将成本函数在θ的当前值附近线性化,得到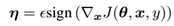 的最优最大范数约束扰动。这个方法是通过使成本函数J(θ,x,y)变大从而达到目的。对这个公式的解释可以参照图4.1:
的最优最大范数约束扰动。这个方法是通过使成本函数J(θ,x,y)变大从而达到目的。对这个公式的解释可以参照图4.1:
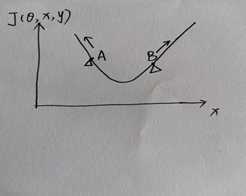
图4.1
图4.1展示了成本函数J(θ,x,y)随输入x变化的图像。选取两个点A、B, A点的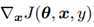 方向为负方向,B点的
方向为负方向,B点的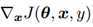 方向为正方向,根据公式
方向为正方向,根据公式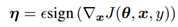 得出A点的为负值,B点的η为正值,所以根据
得出A点的为负值,B点的η为正值,所以根据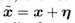 ,可知A点朝x减小的方向移动,B点朝x增加的方向移动,这样的移动都会使成本函数J(θ,x,y)增大,从而达到对抗样本使模型错误分类的目的。
,可知A点朝x减小的方向移动,B点朝x增加的方向移动,这样的移动都会使成本函数J(θ,x,y)增大,从而达到对抗样本使模型错误分类的目的。
但是对于这个方法,还有一些疑问,当梯度方向为0时,成本函数J(θ,x,y)既可能处于极小值也可能处于极大值,当处于C点时,我认为并不能达到对抗样本的攻击目的,见图4.2,所以我认为这种方法有一定的弊端。
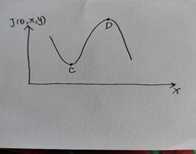
图4.2
通过在ImageNet上的实验,表明这种方法确实会导致各种各样的模型对它们的输入进行错误分类,如图4.3,添加扰动后,熊猫被分类器错误分类为长臂猿。使用 ,一个浅层的softmax分类器在MNIST测试集上的错误率为99.9%,平均置信度为79.3%。在相同的设置下,maxout网络错,误地分类了89.4%的对抗样本,平均置信度为97.6%。类似地,使用
,一个浅层的softmax分类器在MNIST测试集上的错误率为99.9%,平均置信度为79.3%。在相同的设置下,maxout网络错,误地分类了89.4%的对抗样本,平均置信度为97.6%。类似地,使用 ,获得的错误率为87.15%,在CIFAR-10的预处理版本测试集上使用卷积maxout网络时分配给不正确标签的平均概率为96.6%。
,获得的错误率为87.15%,在CIFAR-10的预处理版本测试集上使用卷积maxout网络时分配给不正确标签的平均概率为96.6%。
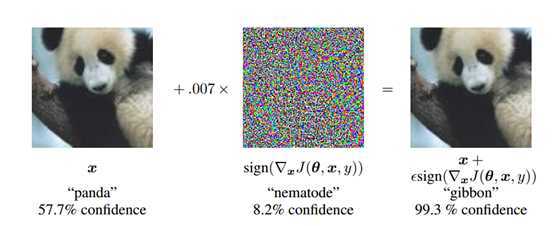
图4.3
这部分内容提出将FGSM应用于逻辑回归,如图5.1(c)展示了对3和7判别任务的逻辑回归模型错误率为1.6%,(d)展示了通过 的FGSM方法实现后对3和7判别任务的逻辑回归模型错误率达到了99%,充分肯定了对抗样本的攻击性。
的FGSM方法实现后对3和7判别任务的逻辑回归模型错误率达到了99%,充分肯定了对抗样本的攻击性。

图5.1
如果我们训练一个单一的模型来识别标签y∈{-1,1}和![]() ,其中
,其中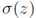 是sigmoid函数,那么训练包括对
是sigmoid函数,那么训练包括对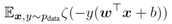 的梯度下降,其中
的梯度下降,其中![]()
是softplus函数。基于梯度符号扰动,可以推导出一个简单的形式来训练最坏情况下x的对抗性扰动,而不是x本身。注意梯度的符号是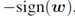 , 并且
, 并且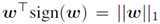 。因此,对抗性的逻辑回归是最小化
。因此,对抗性的逻辑回归是最小化![]() 。具体的推导过程如下图5.2:
。具体的推导过程如下图5.2:
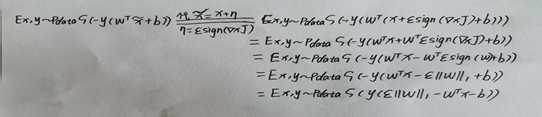
图5.2
最终期望的结果有点类似于L1正则化,但是有一定的区别。L1正则化是加上惩罚项,而对抗训练是减去惩罚项![]() ,在置信度很高的情况下,惩罚项 对整体函数的作用就很小了,不影响整体结果,如果置信度不够高,减去惩罚项就会使结果更小,与真实值就更能区分开。所以L1正则化是会高估扰动造成的影响,而对抗训练则不会,这有利于我们抵抗对抗样本的攻击。
,在置信度很高的情况下,惩罚项 对整体函数的作用就很小了,不影响整体结果,如果置信度不够高,减去惩罚项就会使结果更小,与真实值就更能区分开。所以L1正则化是会高估扰动造成的影响,而对抗训练则不会,这有利于我们抵抗对抗样本的攻击。
深层网络被认为容易受到对抗样本的攻击,这部分提出将FGSM应用于深层神经网络的对抗训练,发现基于快速梯度符号法的对抗性目标函数训练是一种有效的正则化方法: ![]() ,使用这个公式的好处是使每一次训练都有新的对抗样本的参与,达到了对抗训练的目的。
,使用这个公式的好处是使每一次训练都有新的对抗样本的参与,达到了对抗训练的目的。
在所有的实验中,使用最初对这个超参数的猜测做得很好,以至于没有必要进行更多的探索。这种方法意味着不断地更新提供的对抗样本,以使它们抵制模型的当前版本,这里有点生成对抗网络的感觉。使用这种方法来训练一个maxout网络,该网络也用dropout进行了正则化,能够将错误率从没有经过对抗训练的0.94%降低到经过对抗训练的0.84%。
通过对论文的学习,我们可以发现:尽管我们很不习惯观察高维空间,但我们不得不承认对抗性例子是真实存在的。对抗性的例子可以解释为高维点积的一个性质,它们是神经网络模型过于线性化的结果,而不是过于非线性的结果。在高维空间中,线性行为很容易引起对抗性例子。在不同的模型之间推广对抗性的例子可以解释为对抗性扰动与模型的权向量高度一致,以及不同的模型在训练执行相同的任务时学习相似的函数的结果。对于论文提到的FGSM方法,找到扰动的方向,比找到空间中的特定点更加重要,因此对抗性扰动可以推广到不同的clean examples(净例子)上。论文也特别指出了RBF网络能够抵抗对抗性例子,接受过输入分布建模训练的模型无法抵抗对抗性的例子。
对抗性例子的存在表明,能够解释训练数据,甚至能够正确标记测试数据,并不意味着我们的模型真正理解了我们要求它们执行的任务。相反,它们的线性响应在数据分布中不出现的点上过于自信,而这些自信的预测通常是高度不正确的。这项工作表明,我们可以通过明确地识别有问题的点并在每个点上修正模型来部分地纠正这个问题。然而,有一个人可能也会得出这样的结论:我们使用的模式家庭本质上是有缺陷的。优化的容易是以模型容易被误导为代价的。这推动了优化过程的发展,使其能够训练行为更局部稳定的模型。
论文中提到的FGSM是第一个基于梯度的攻击,后期基于梯度的攻击几乎都是在此方法上进行改进。其缺陷在于将梯度加到原图片这个操作仅仅进行了一次,如果网络是线性的,这样一次操作即可达到效果(因为攻击的方向是对的),但如果网络是非线性的,那么攻击的方向仅仅在某一点是对的(即在某点处时,梯度上升最快的方向是对的),但这并不意味着loss就增大了很多(即走完一步后的位置的梯度最大方向和原来就不一样了)。BTW,FGSM虽然白盒攻击比其他的攻击差,但迁移攻击效果不一定比其它的攻击差,这是因为,FGSM攻击比较粗糙,只是给出了大致的攻击方向,那么这对于迁移来说是合适的。
[1] 张岩琪.《Maxout Networks》论文阅读[EB/OL].https://zhuanlan.zhihu.com/p/31685211,2017-12-14.
[2] Williamongh.RBF(径向基函数)神经网络[EB/OL].https://www.jianshu.com/p/b4434a955e83,2018-12-03.
[3] 禅在心中.RBF(径向基)神经网络[EB/OL].https://www.cnblogs.com/pinking/p/9349695.html,2018-07-22.
[4] bitcarmanlee.小白都能看懂的softmax详解[EB/OL].https://blog.csdn.net/bitcarmanlee/article/details/82320853,2018-09-02.
[5] 机器学习安全小白.基于梯度的攻击——FGSM[EB/OL].https://www.cnblogs.com/tangweijqxx/p/10615950.html,2019-03-28.
[6] Eigenvalue.对抗样本的解释与掌控[EB/OL].https://zhuanlan.zhihu.com/p/76937330,2019-08-06.
《Explaining and harnessing adversarial examples》 论文学习报告
原文:https://www.cnblogs.com/gris3/p/12582303.html