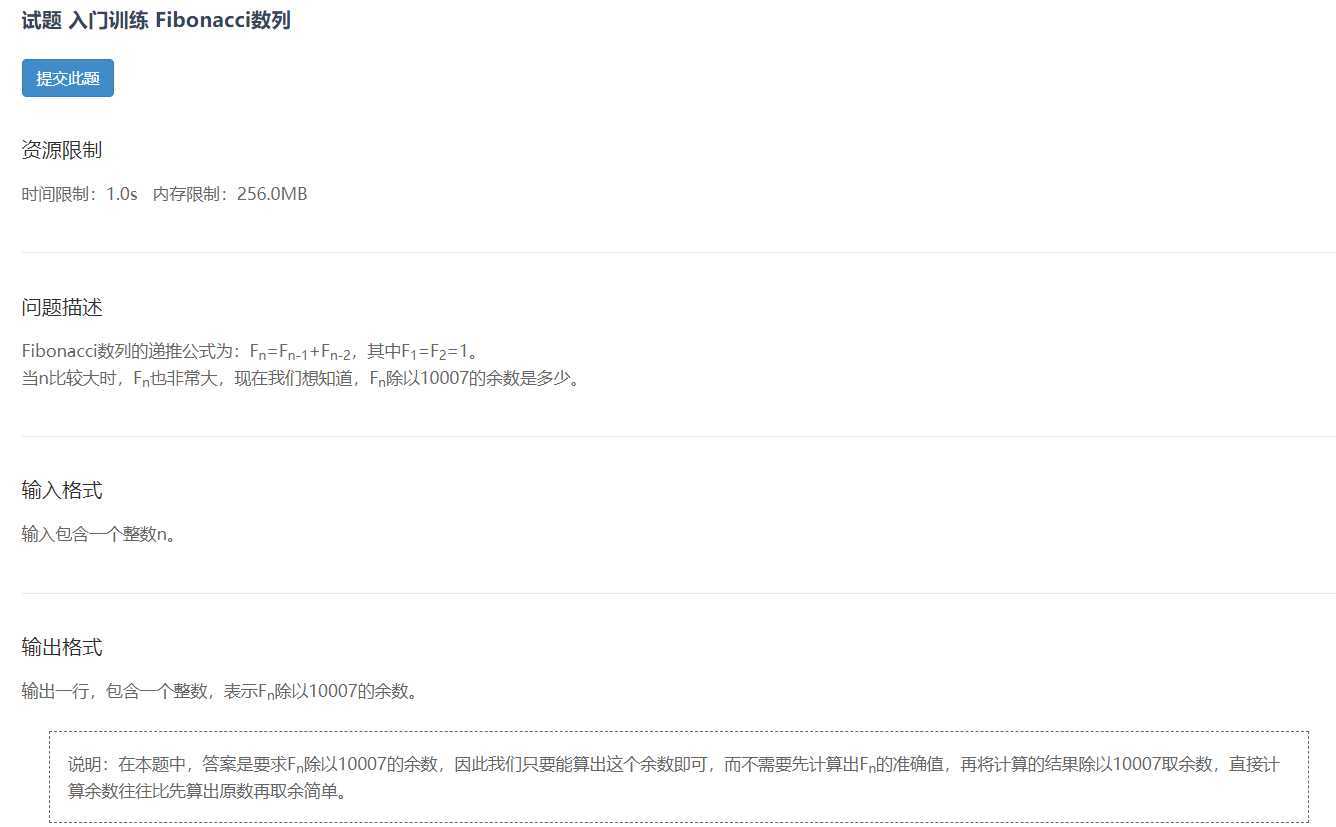
第一步:了解问题的数据规模
由题可以看出n的范围比较大,Fn的范围也很大,所以我们的数据类型尽量考虑long型,同时也排除用递归的解法,因为递归的解法时间复杂度比较高
第二步:选择合适的解法
解法1:开辟数组的解法(具体思路在代码中呈现)
解法2:滚动数组的解法(具体思路在代码中呈现)
这里我优先考虑用滚动数组的解法,因为时间复杂度O(n)级别,空间复杂度为O(1)级别,即能节省空间,又能节省时间
代码实现:
//开辟数组的方式 public static long fib1 (int n){ //由于是从1开始而且还要最少存储3个元素因此数组长度为n+2. long[] fibs = new long[n+2]; fibs[0] = 0; fibs[1] = 1; fibs[2] = 1; // 从第三个开始遍历, fibs[0] = 0;用不到 for (int i = 3; i <=n; i++) { // 只存储余数即可 fibs[i] = (fibs[i-1] + fibs[i-2]) % 10007; } return fibs[n]; }
//滚动数组的方式 public static long fib2(int n){ //创建一个长度为3的滚动数组,并进行初始化 long[] fibs ={0,1,1}; //由于n=1时和n=2时不用进行滚动,所以直接返回就行 if(n==1||n==2) return 1; //由于第1次滚动会得出n=3的fib数,第2次滚动会得出n=4的fib数,所以第n-2次滚动会得出n的fib数 for(int i=1;i<=n-2;i++){ fibs[0]=fibs[1]; fibs[1]=fibs[2]; fibs[2]=(fibs[0]+fibs[1])%10007; //根据题意,只存储余数即可 } return fibs[2]; }
2020-03-27
原文:https://www.cnblogs.com/songchengyu/p/12582756.html