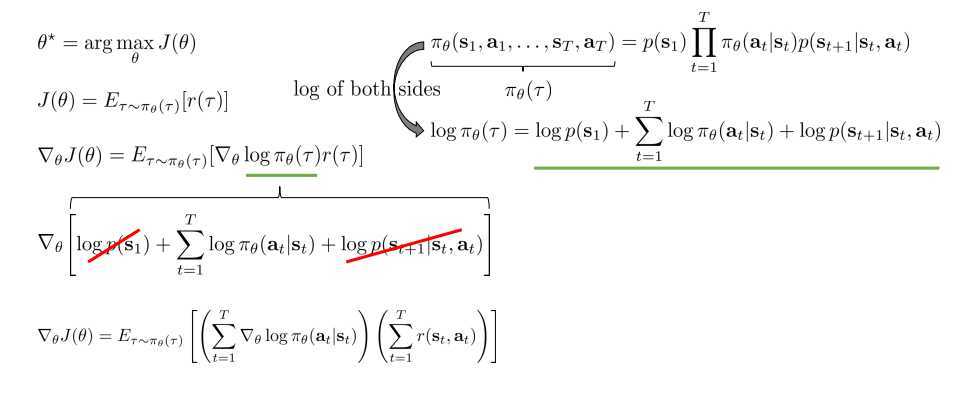策略梯度
value based的强化学习方法对价值函数进行了近似表示,policy based使用了类似的思路,策略\(\pi\)可以被描述为一个包含参数\(\theta\)的函数
\[\pi_{\theta}(s, a)=P(a | s, \theta) \approx \pi(a | s)
\]
我们可以假设有一个策略\(\pi_\theta(a|s)\),那么我们其实有一个概率\(p(s‘|s,a)\),表示状态转移概率,它受参数\(\theta\)的影响,整条路径可以用\(\tau\)表示,
\[\underbrace{p_{\theta}\left(\mathbf{s}_{1}, \mathbf{a}_{1}, \ldots, \mathbf{s}_{T}, \mathbf{a}_{T}\right)}_{p_{\theta}(\tau)}=p\left(\mathbf{s}_{1}\right) \prod_{t=1}^{T} \pi_{\theta}\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right) p\left(\mathbf{s}_{t+1} | \mathbf{s}_{t}, \mathbf{a}_{t}\right)
\]
那么我们的目的就是优化\(\theta\)使得期望总回报最大,
\[\theta^* = arg\max_\theta E_{\tau\sim p_\theta(\tau)} \left[\sum_t\gamma(s_t,a_t)\right]
\]
由于我们没有办法直接计算出期望总回报,只能通过与环境的交互,通过多次采样来获得期望值。
由此我们可以得到类似机器学习里的目标函数,并且用多次取样来近似计算它
\[J(\theta)=E_{\tau\sim p_\theta(\tau)} \left[\sum_t\gamma(s_t,a_t)\right]\approx \frac{1}{N}\sum_{i=1}^N \sum_t \gamma(s_{i,t},a_{i,t})
\]
slide有些不一致,\(p_\theta(\tau)\)和\(\pi_\theta(\tau)\)等价,都是表示一个策略,经过一系列推导可以求得目标函数的导数
\[\nabla_\theta J(\theta) = E_{\tau \sim \pi_{\theta}(\tau)}\left[\nabla_{\theta} \log \pi_{\theta}(\tau) r(\tau)\right]
\]
我们可以经过一系列推导并移除式子中导数为0的项以得到更确切的公式:
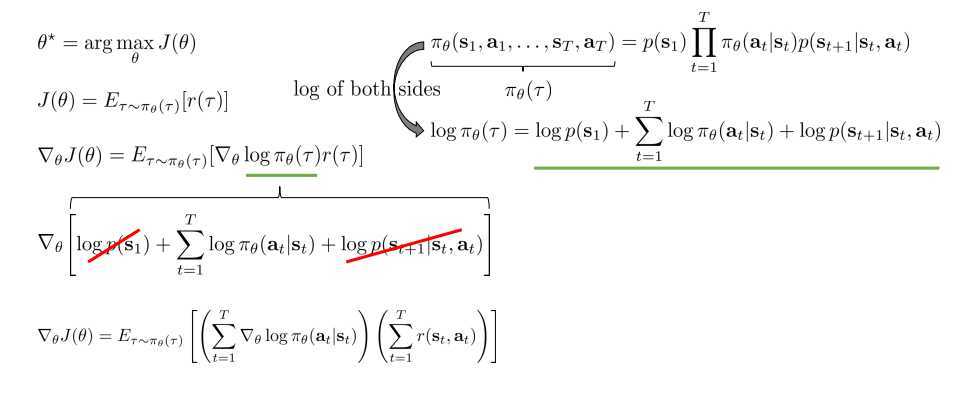
\[\nabla_{\theta} J(\theta)=E_{\tau \sim \tau_{*}(\tau)}\left[\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t} | \mathbf{s}_{t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right)\right]
\]
有了上面的梯度公式,我们就可以给定初始\(\theta\)和环境交互得到目标函数的梯度来增大期望回报。也即是说,通过采样来更新\(\theta\)。
那么策略\(\pi\)具体是什么形式呢?
在离散行为空间中常用softmax策略函数,因为策略需要满足对于任意状态\(s \in S\) 均有\(\sum_a\pi(a|s)=1\),为此,引入动作偏好函数,利用 动作偏好的softmax值作为策略
\[\pi(a | S ; \theta)=\frac{e^ {h(s, a ; \theta)}}{\sum_{a^{\prime}} e^ {h\left(s, a^{\prime} ; \theta\right)}}
\]
则可以求出相应分值函数的导数
\[\nabla_{\theta} \log \pi_{\theta}(s, a)=\phi(s, a)-\mathbb{E}_{\pi \theta}[\phi(s, a)]
\]
在连续行为空间中常用高斯策略,其行为从高斯分布\(
\mathbb{N}\left(\phi(\mathbf{s})^{\mathrm{T}_\theta} , \sigma^{2}\right)
\)中产生,其对应log函数的导数
\[\nabla_{\theta} \log \pi_{\theta}(s, a)=\frac{\left(a-\phi(s)^{T_\theta} \right) \phi(s)}{\sigma^{2}}
\]
之前提到的
\[J(\theta)=E_{\tau\sim p_\theta(\tau)} \left[\sum_t\gamma(s_t,a_t)\right]\approx \frac{1}{N}\sum_{i=1}^N \sum_t \gamma(s_{i,t},a_{i,t})
\]
采样N次后可以估计出目标函数的梯度
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} | \mathbf{s}_{i, t}\right)\right)\left(\sum_{t=1}^{T} r\left(\mathbf{s}_{i, t}, \mathbf{a}_{i, t}\right)\right)
\]
截至目前,我们就可以给出我们的强化学习算法:
- sample \(\{\tau^i\}\) from \(\pi_\theta(a_t|s_t)\) (run the policy)
- 用上面的梯度公式计算梯度
- \(\theta \leftarrow \theta+\alpha\nabla_\theta J(\theta)\)
或许你看到会有疑问——策略\(\pi_\theta(a_t|s_t)\)具体是什么?我们可以举一个自动驾驶的例子,策略的状态s就是当前道路情况,动作a就是左转、右转、执行,参数\(\theta\)就是神经网络的权重、偏置。
由于采样的不确定性,前面的算法会有很大的方差。
那么如何减小算法的方差呢??
一个基本的原则是policy at time t‘ can not affect reward at time t when t < t‘(后面的策略不会影响之前的奖励)

\(\hat{Q}_{i,t}\)代表在第\(i\)次取样中从\(t\)时刻到最后获得的reward的和
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} | \mathbf{s}_{i, t}\right) \hat{Q}_{i, t}
\]
还有一项改进是Baseline
强化学习的目的是增加好的选择的概率减少坏的选择的概率,那么如果一个好的动作的reward是10001,坏的选择的reward是10000,那么学习的效果就会不明显。一个显而易见的改进是在奖励中减去平均值
\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \nabla_\theta \log \pi_\theta(\tau) \left[\gamma(\tau)-b \right]
\]
\[b = \frac{1}{N} \sum_{i=1}^N \gamma(\tau)
\]
Policy gradient is on-policy
这意味着每次你更改策略都需要重新和环境交互采样获得新的样本。
pytorch实现REINFORCE的代码https://github.com/pytorch/examples/blob/master/reinforcement_learning/reinforce.py
强化学习 策略梯度
原文:https://www.cnblogs.com/lepeCoder/p/RL_PolicyGradients.html