题目链接:https://www.luogu.com.cn/problem/P3388
tarjan算法果然牛逼,时间复杂度是O(|V|+|E|),所以1e4个结点2e5条边的图完全不在话下orz orz
一个无向图求割点,该图不一定连通,所以要对没有访问过的点继续tarjan,这时候我就wa了几次,因为之前只用过一次tarjan,在参数设置里面我默认了从u=1开始建dfs树。每次只有根节点的father值等于其编号,这样就能唯一地标识它,学到了。其次在下面证明 tarjan中如果在处理回退边的时候用的是①、 low[u]=min(low[u],low[v])(强连通分量的用法)而不是②、low[u]=min(low[u],dfn[v])的话将会出现什么样的错误。
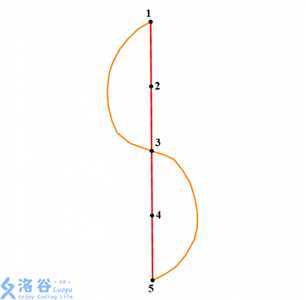
我们模拟两种Tarjan算法,一种是low[u] = min( low[u], low[v] );,一种是low[u] = min( low[u], dfn[v] );。(证明参考洛谷博客)
第1种:
① dfs(1),dfn[1] = 1,low[1] = 1。
② dfs(2),dfn[2] = 2,low[2] = 2。
③ dfs(3),dfn[3] = 3,low[3] = 3。
④ 发现回边 3 -> 1,low[3] = 1。
⑤ dfs(4),dfn[4] = 4,low[4] = 4。
⑥ dfs(5),dfn[5] = 5,low[5] = 5。
⑦ 发现回边 5 -> 3,low[5] = 1。
⑧ dfs(5)结束,回到dfs(4),low[4] = 1。
⑨ dfs(4)结束,回到dfs(3),low[3] = 1。
⑩ dfs(3)结束,至此未发现割点。
第2种:
① dfs(1),dfn[1] = 1,low[1] = 1。
② dfs(2),dfn[2] = 2,low[2] = 2。
③ dfs(3),dfn[3] = 3,low[3] = 3。
④ 发现回边 3 -> 1,low[3] = 1。
⑤ dfs(4),dfn[4] = 4,low[4] = 4。
⑥ dfs(5),dfn[5] = 5,low[5] = 5。
⑦ 发现回边 5 -> 3,low[5] = 3。
⑧ dfs(5)结束,回到dfs(4),low[4] = 3。
⑨ dfs(4)结束,回到dfs(3),low[4] >= dfn[3],发现割点3,low[3] = 1。
而这个图中,正确答案是:3是割点。
所以第1种方法就被我们愉快地Hack掉了。
其次,我在处理回退边的时候在条件中加上了dfn[v]<dfn[u],时间效率提高了大约10%,这是显而易见的,因为只有回退边到达的结点在父节点之前被访问,而且这个结点还不是已经处理过的fa结点。
代码如下:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef unsigned int ui; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 #define pf printf 7 #define mem(a,b) memset(a,b,sizeof(a)) 8 #define prime1 1e9+7 9 #define prime2 1e9+9 10 #define pi 3.14159265 11 #define lson l,mid,rt<<1 12 #define rson mid+1,r,rt<<1|1 13 #define scand(x) scanf("%llf",&x) 14 #define f(i,a,b) for(int i=a;i<=b;i++) 15 #define scan(a) scanf("%d",&a) 16 #define mp(a,b) make_pair((a),(b)) 17 #define P pair<int,int> 18 #define dbg(args) cout<<#args<<":"<<args<<endl; 19 #define inf 0x3f3f3f3f 20 const int maxn=2e4+10; 21 int n,m,t; 22 inline int read(){ 23 int ans=0,w=1; 24 char ch=getchar(); 25 while(!isdigit(ch)){if(ch==‘-‘)w=-1;ch=getchar();} 26 while(isdigit(ch))ans=(ans<<3)+(ans<<1)+ch-‘0‘,ch=getchar(); 27 return ans*w; 28 } 29 int low[maxn],dfn[maxn],iscut[maxn],head[maxn],nxt[200010]; 30 int cnt=0; 31 int ans=0; 32 struct node{ 33 int u,v; 34 }p[200010]; 35 int e=0; 36 void addedge(int x,int y) 37 { 38 p[e].u=x; 39 p[e].v=y; 40 nxt[e]=head[x]; 41 head[x]=e++; 42 } 43 void tarjan(int u,int fa) 44 { 45 dfn[u]=low[u]=++cnt; 46 int child=0; 47 for(int i=head[u];~i;i=nxt[i]) 48 { 49 int v=p[i].v; 50 if(!dfn[v]) 51 { 52 if(fa==u)child++; 53 tarjan(v,u); 54 low[u]=min(low[v],low[u]); 55 if(low[v]>=dfn[u]&&u!=fa)iscut[u]=1; 56 } 57 else if(dfn[v]<dfn[u]&&v!=fa) 58 { 59 low[u]=min(low[u],dfn[v]); 60 } 61 } 62 if(u==fa&&child>1)iscut[u]=1; 63 } 64 int main() 65 { 66 //freopen("input.txt","r",stdin); 67 //freopen("output.txt","w",stdout); 68 std::ios::sync_with_stdio(false); 69 n=read(),m=read(); 70 int x,y; 71 cnt=0; 72 ans=0; 73 mem(low,0); 74 mem(dfn,0); 75 mem(iscut,0); 76 mem(head,-1); 77 mem(nxt,-1); 78 f(i,1,m) 79 { 80 x=read(),y=read(); 81 addedge(x,y); 82 addedge(y,x); 83 } 84 f(i,1,n) 85 { 86 if(!dfn[i])tarjan(i,i);//图不一定连通,所以每个连通分量都要tarjan一次 87 } 88 f(i,1,n) 89 { 90 if(iscut[i])ans++; 91 } 92 pf("%d\n",ans); 93 f(i,1,n) 94 if(iscut[i])pf("%d ",i); 95 return 0; 96 }
原文:https://www.cnblogs.com/randy-lo/p/12583899.html