在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。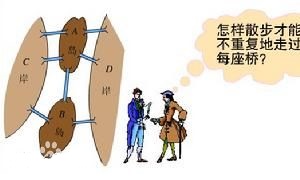
能否走过这样的七座桥,并且每桥只走一次?瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡七桥问题,并证明了更为广泛的有关一笔画的三条结论,人们通常称之为欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。
你的任务是:对于给定的一组无向图数据,判断其是否成其为欧拉图?
1 6 10 1 2 2 3 3 1 4 5 5 6 6 4 1 4 1 6 3 4 3 6
1
1 #include<stdio.h> 2 #include<string.h> 3 int d[1010],f[1010]; 4 int t,n,m; 5 int find(int x) 6 { 7 if(x!=f[x]) 8 f[x]=find(f[x]); 9 return f[x]; 10 } 11 void check(int x,int y) 12 { 13 int fx=find(x); 14 int fy=find(y); 15 if(fx!=fy) 16 f[fx]=fy; 17 } 18 int solve() 19 { 20 int cnt=0; 21 for(int i=1; i<=n; ++i) 22 { 23 if(f[i]==i) 24 cnt++; 25 } 26 if(cnt!=1) 27 return 0; 28 for(int i=1;i<=n;++i) 29 { 30 if(d[i]%2==1) 31 return 0; 32 } 33 return 1; 34 } 35 int main() 36 { 37 int t; 38 scanf("%d",&t); 39 while(t--) 40 { 41 scanf("%d%d",&n,&m); 42 for(int i=1; i<=n; ++i) 43 { 44 f[i]=i; 45 d[i]=0; 46 } 47 int u,v; 48 for(int i=0; i<m; ++i) 49 { 50 scanf("%d%d",&u,&v); 51 check(u,v); 52 d[u]++; 53 d[v]++; 54 } 55 if(solve()) 56 printf("1\n"); 57 else 58 printf("0\n"); 59 } 60 return 0; 61 }
解法二:DFS
1 #include<stdio.h> 2 #include<string.h> 3 int map[1010][1010],visited[10100],sum,d[2000],n; 4 void DFS(int x) 5 { 6 int i; 7 visited[x]=1; 8 sum++; 9 for(i=1;i<=n;i++) 10 if(visited[i]==0&&map[x][i]) 11 DFS(i); 12 } 13 int main() 14 { 15 int i,j,m,k,t,l1,l2; 16 scanf("%d",&t); 17 while(t--) 18 { 19 sum=0; 20 memset(map,0,sizeof(map)); 21 memset(visited,0,sizeof(visited)); 22 memset(d,0,sizeof(d)); 23 scanf("%d %d",&n,&m); 24 for(i=0;i<m;i++) 25 { 26 scanf("%d %d",&l1,&l2); 27 map[l1][l2]=1; 28 map[l2][l1]=1; 29 d[l1]++; 30 d[l2]++; 31 } 32 DFS(l1); 33 for(i=1;i<=n;i++) 34 if(d[i]%2==1) 35 break; 36 if(i==n+1&&sum==n) 37 printf("1\n"); 38 else 39 printf("0\n"); 40 } 41 }
解法三:bfs
1 #include<stdio.h> 2 #include<string.h> 3 int map[1010][1010],visited[10100],sum,d[2000],d1[2000],n; 4 void BFS(int s) 5 { 6 int out=0,in=0,v,i; 7 visited[s]=1; 8 sum++; 9 d1[in++]=s; 10 while(out<in) 11 { 12 v=d1[out++]; 13 for(i=1;i<=n;i++) 14 if(visited[i]==0&&map[v][i]) 15 { 16 visited[i]=1; 17 sum++; 18 d1[in++]=i; 19 } 20 } 21 } 22 int main() 23 { 24 int i,j,m,k,t,l1,l2; 25 scanf("%d",&t); 26 while(t--) 27 { 28 sum=0; 29 memset(map,0,sizeof(map)); 30 memset(visited,0,sizeof(visited)); 31 memset(d,0,sizeof(d)); 32 scanf("%d %d",&n,&m); 33 for(i=0;i<m;i++) 34 { 35 scanf("%d %d",&l1,&l2); 36 map[l1][l2]=1; 37 map[l2][l1]=1; 38 d[l1]++; 39 d[l2]++; 40 } 41 BFS(1); 42 for(i=1;i<=n;i++) 43 if(d[i]%2==1) 44 break; 45 if(i==n+1&&sum==n) 46 printf("1\n"); 47 else 48 printf("0\n"); 49 } 50 }
原文:https://www.cnblogs.com/xiaolitongxueyaoshangjin/p/12584009.html