原文:https://blog.csdn.net/czyt1988/article/details/84995295
FFT之后得到的那一串复数是波形对应频率下的幅度特征,注意这个是幅度特征不是幅值。
获取频率:
傅里叶变换并没对频率进行任何计算,频率只与采样率和进行傅里叶变换的点数相关。
FFT变换完的第一个数对应0Hz,即直流分量。后面第二个复数对应的频率是0Hz+频谱分辨率,每隔一个加一次,直到$\frac{N}{2}$个数,频谱分辨率$\Delta f $计算公式如下:\[\Delta f{\rm{ = }}\frac{{Fs}}{N}\]其中$Fs$为采样率,$N$为FFT的点数。
获取幅值:
假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的$\frac{N}{2}$倍。而第一个点就是直流分量,它的模值是直流分量的$N$倍。
要得出真实幅值,需要把除了第1个点(i=1)以及最后一个点(i=N/2)除以N以外,其余点需要用求得的模除以$\frac{N}{2}$。实际应用中,只有$i = 1$~$\frac{N}{2}$是有用的。
函数:
function [Fre,Amp,Ph] = FFT(data,Fs,ampDB,isDetrend)
% 快速傅里叶变换
% data:波形数据
% Fs:采样率
% ampDB:逻辑值,是否进行对数变换,默认为false
% isDetrend:逻辑值,是否进行去均值处理,默认为true
% 返回[Fre:频率,Amp:幅值,Ph:相位(弧度)]
if nargin<3
ampDB=false;
isDetrend=true;
elseif nargin<4
isDetrend=true;
end
n=length(data);
if mod(n,2)==1
n=n-1;
data=data(1:n);
end
if isDetrend
data=detrend(data);
end
Y = fft(data);
%频率
Fre=(0:n-1)*Fs/n;
Fre=Fre(1:n/2);
%幅值
Amp=abs(Y(1:n/2));
Amp([1,n/2])=Amp([1,n/2])/n;
Amp(2:n/2-1)=Amp(2:n/2-1)/(n/2);
if ampDB
Amp=20*log(Amp);
Amp(Amp<0)=0;
end
%相位
Ph=angle(Y(1:n/2));
end
调用示例:
%生成信号
N = 256;
Fs = 150;
t = (0:N-1)./Fs;
wave = 5 + 8*cos(2*pi*10.*t) ...
+ 4*cos(2*pi*20.*t + deg2rad(30)) ...
+ 2*cos(2*pi*30.*t + deg2rad(60)) ...
+ 1*cos(2*pi*40.*t + deg2rad(90)) ...
+ rand(1,length(t)) ...
;
[Fre,Amp,~]=FFT(wave,Fs,false,false);
plot(t,wave);
局部放大:
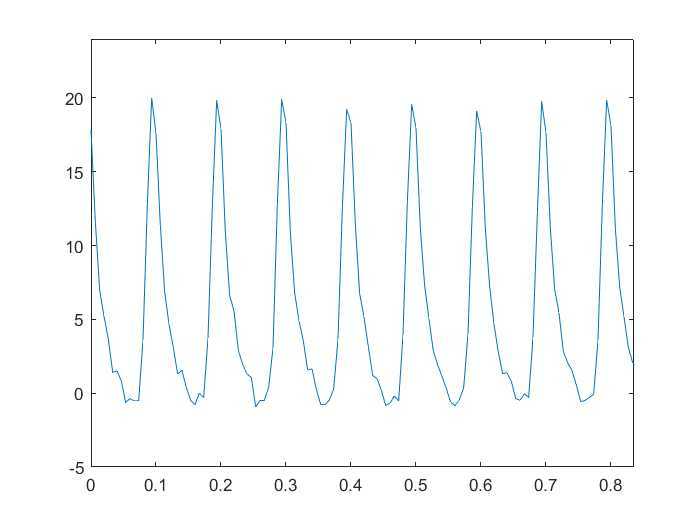
plot(Fre,Amp);
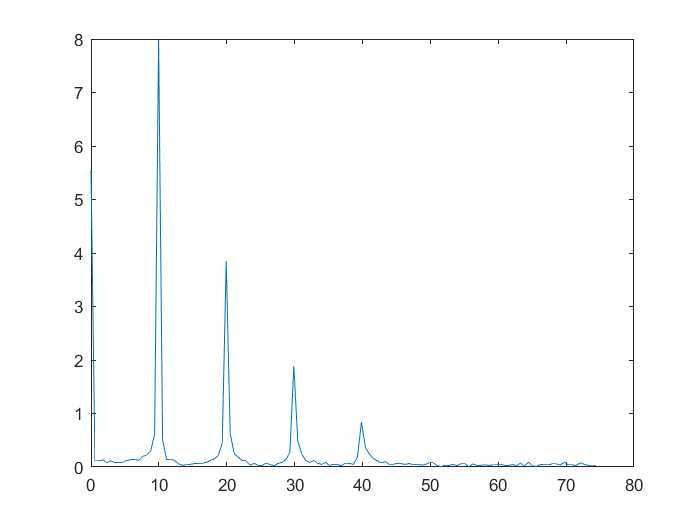
以全波桥式整流电路(Full-Wave Bridge Rectifier)为例。
在MATLAB命令窗口中运行ssc_bridge_rectifier即可打开示例。
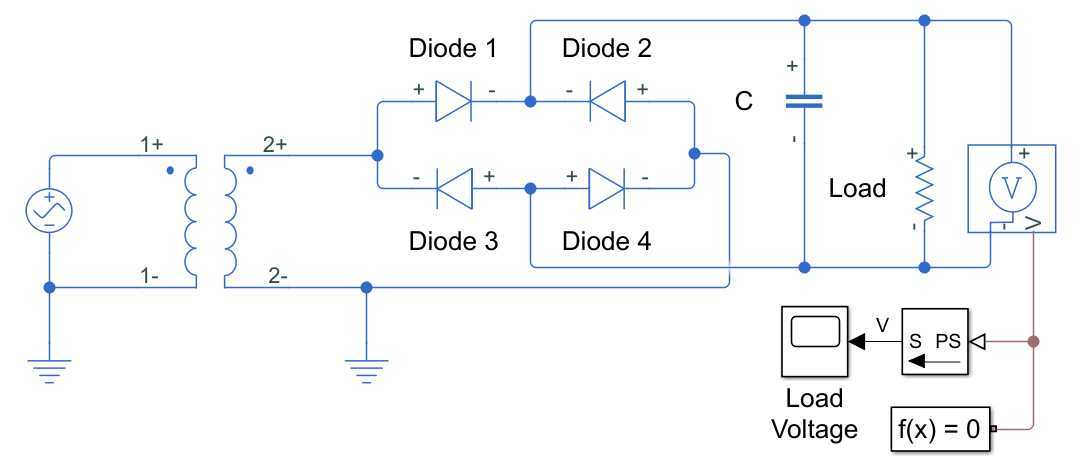
改为固定步长:

仿真时间0.15s:
示波器数据保存到工作区,命名为Vout:

运行仿真:
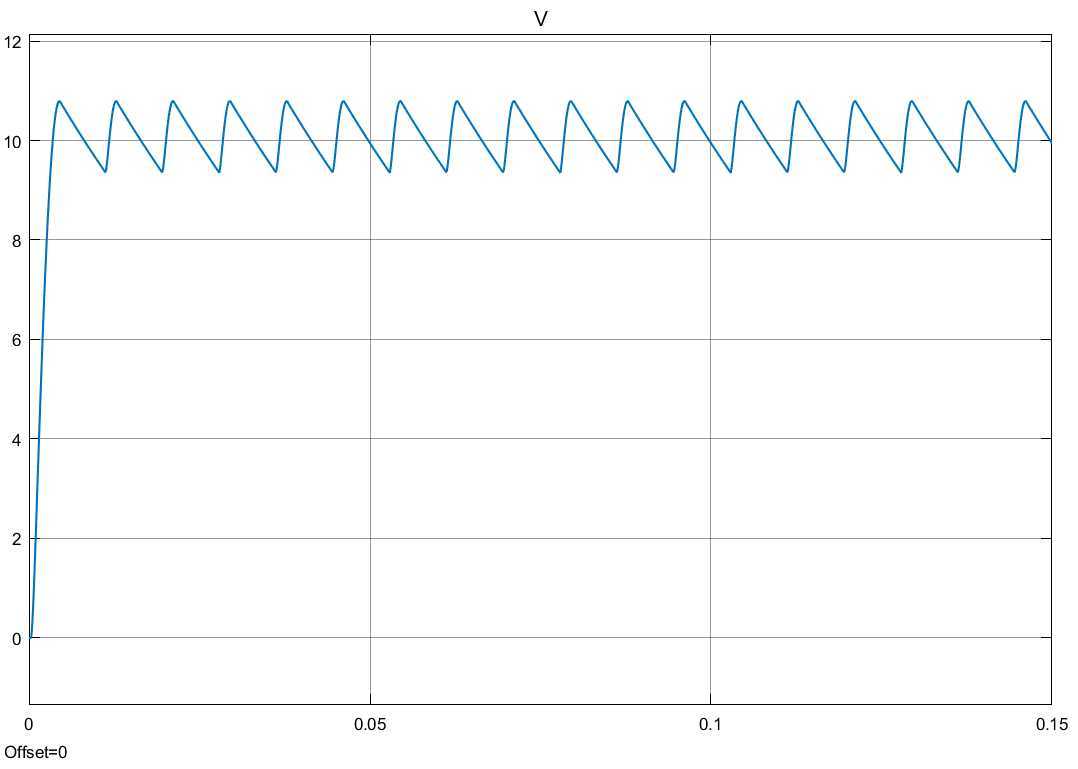
工作区分析:
[FreV,AmpV,PhV]=FFT(Vout.signals.values(201:1501),1e4); plot(FreV,AmpV); xlim([0 1000]);
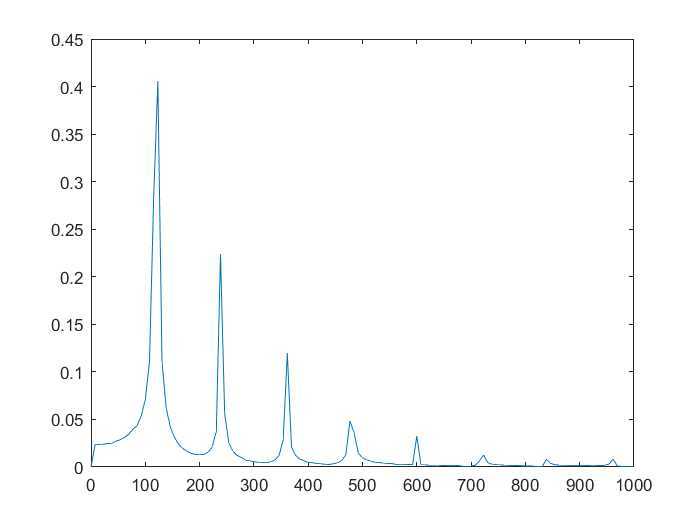
powergui→Tools→FFT Analysis:

选取对应的信号输入,开始时间,基频,周期等参数即可得到FFT分析结果,同时还有总谐波失真THD。
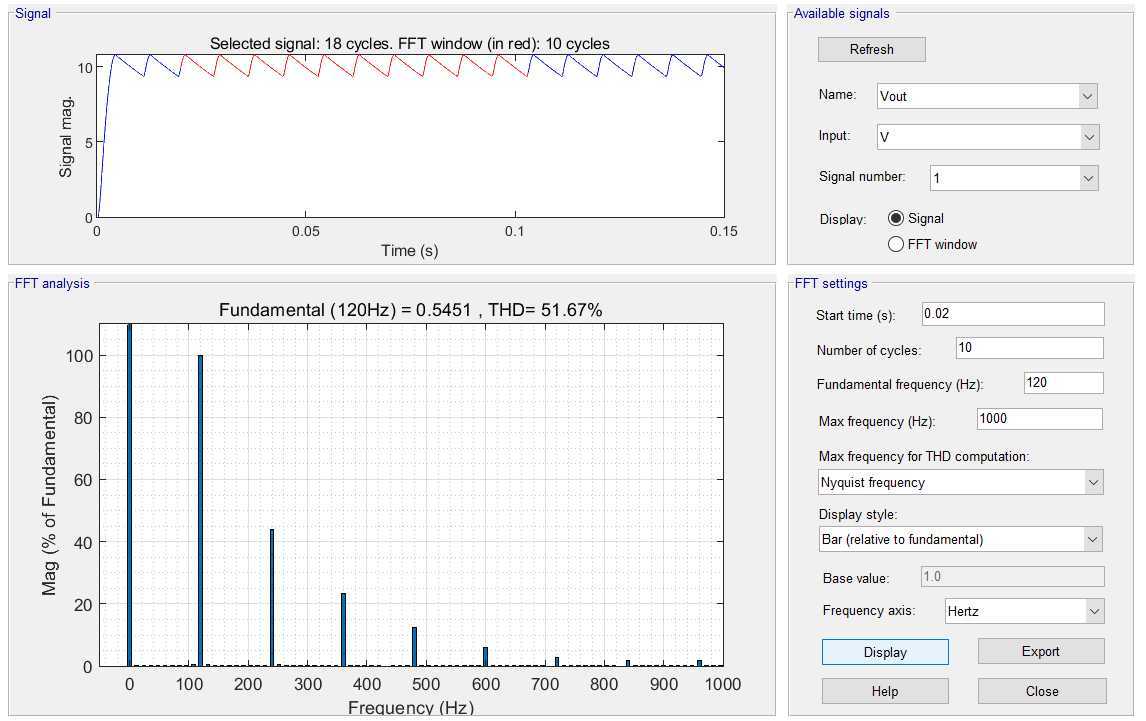
可以看到此结果与前面的一致。
函数:
FFT<-function(data,Fs,ampDB=FALSE,isDetrend=TRUE)
{
# 快速傅里叶变换
# data:波形数据
# Fs:采样率
# ampDB:逻辑值,是否进行对数变换,默认为false
# isDetrend:逻辑值,是否进行去均值处理,默认为true
# 返回[Fre:频率,Amp:幅值,Ph:相位(弧度)]
n=length(data)
if(n%%2==1)
{
n=n-1
data=data[1:n]
}
if(isDetrend)
{
data<-scale(data,center=T,scale=F)
}
library(stats)
Y = fft(data)
#频率
Fre=(0:(n-1))*Fs/n
Fre=Fre[1:(n/2)]
#幅值
Amp=Mod(Y[1:(n/2)])
Amp[c(1,n/2)]=Amp[c(1,n/2)]/n
Amp[2:(n/2-1)]=Amp[2:(n/2-1)]/(n/2)
if(ampDB)
{
Amp=20*log(Amp)
Amp[Amp<0]=0
}
#相位
Ph=Arg(Y[1:(n/2)])
result<-data.frame(Fre=Fre,Amp=Amp,Ph=Ph)
return(result)
}
示例:
#生成信号
deg2rad<-function(a)
{
return(a*pi/180)
}
N = 256
Fs = 150
t = (0:(N-1))/Fs
wave = 5 + 8*cos(2*pi*10.*t) +
4*cos(2*pi*20.*t + deg2rad(30)) +
2*cos(2*pi*30.*t + deg2rad(60)) +
1*cos(2*pi*40.*t + deg2rad(90)) +
rnorm(length(t))
result=FFT(wave,Fs,isDetrend=FALSE)
library(ggplot2)
theme_set(theme_light())
qplot(t,wave,geom="line")
ggplot(data=result,aes(Fre,Amp))+geom_line()
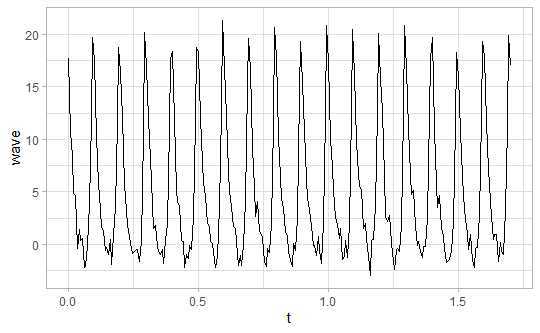
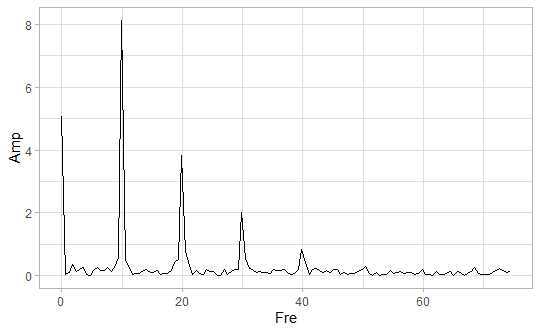
Shiny示例:
原文:https://www.cnblogs.com/dingdangsunny/p/12573744.html