https://codeforces.com/contest/1328/problem/E
E. Tree Queries
You are given a rooted tree consisting of nn vertices numbered from 11 to nn. The root of the tree is a vertex number 11.
A tree is a connected undirected graph with n−1n−1 edges.
You are given mm queries. The ii-th query consists of the set of kiki distinct vertices vi[1],vi[2],…,vi[ki]vi[1],vi[2],…,vi[ki]. Your task is to say if there is a path from the root to some vertex uu such that each of the given kk vertices is either belongs to this path or has the distance 11 to some vertex of this path.
The first line of the input contains two integers nn and mm (2≤n≤2⋅1052≤n≤2⋅105, 1≤m≤2⋅1051≤m≤2⋅105) — the number of vertices in the tree and the number of queries.
Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi, the labels of vertices it connects (1≤ui,vi≤n,ui≠vi(1≤ui,vi≤n,ui≠vi).
It is guaranteed that the given edges form a tree.
The next mm lines describe queries. The ii-th line describes the ii-th query and starts with the integer kiki (1≤ki≤n1≤ki≤n) — the number of vertices in the current query. Then kiki integers follow: vi[1],vi[2],…,vi[ki]vi[1],vi[2],…,vi[ki] (1≤vi[j]≤n1≤vi[j]≤n), where vi[j]vi[j] is the jj-th vertex of the ii-th query.
It is guaranteed that all vertices in a single query are distinct.
It is guaranteed that the sum of kiki does not exceed 2⋅1052⋅105 (∑i=1mki≤2⋅105∑i=1mki≤2⋅105).
For each query, print the answer — "YES", if there is a path from the root to some vertex uu such that each of the given kk vertices is either belongs to this path or has the distance 11 to some vertex of this path and "NO" otherwise.
10 6 1 2 1 3 1 4 2 5 2 6 3 7 7 8 7 9 9 10 4 3 8 9 10 3 2 4 6 3 2 1 5 3 4 8 2 2 6 10 3 5 4 7
YES YES YES YES NO NO
The picture corresponding to the example:
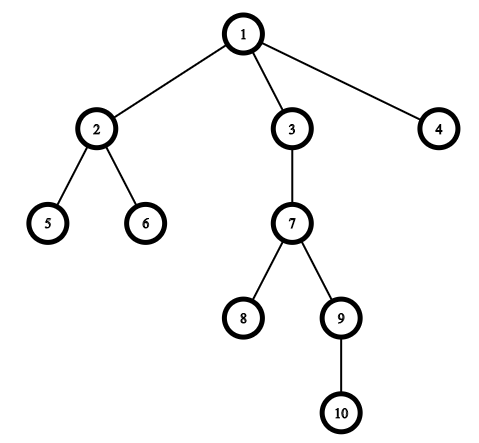
Consider the queries.
The first query is [3,8,9,10][3,8,9,10]. The answer is "YES" as you can choose the path from the root 11 to the vertex u=10u=10. Then vertices [3,9,10][3,9,10] belong to the path from 11 to 1010 and the vertex 88 has distance 11 to the vertex 77 which also belongs to this path.
The second query is [2,4,6][2,4,6]. The answer is "YES" as you can choose the path to the vertex u=2u=2. Then the vertex 44 has distance 11 to the vertex 11 which belongs to this path and the vertex 66 has distance 11 to the vertex 22 which belongs to this path.
The third query is [2,1,5][2,1,5]. The answer is "YES" as you can choose the path to the vertex u=5u=5 and all vertices of the query belong to this path.
The fourth query is [4,8,2][4,8,2]. The answer is "YES" as you can choose the path to the vertex u=9u=9 so vertices 22 and 44 both have distance 11 to the vertex 11 which belongs to this path and the vertex 88 has distance 11 to the vertex 7 which belongs to this path.
The fifth and the sixth queries both have answer "NO" because you cannot choose suitable vertex u.
题目描述:
从顶点1到其他问的各点,能否找出一条路,使得问的点在这条路上或于这条路距离为1.
分析:
记录下每个点的深度,可以看出1到最深的点构成的路是主干,其他的点作为这条路上的分支。求其他点到这条路的距离是否大于1,这个点v与最深的点的公共祖先u,可以看出u最是在在主干上,且与v最近的点。他们的深度差,就是他们的距离。
代码:
#include<iostream> #include<algorithm> #include<cstring> #include<cstdio> #include<sstream> #include<vector> #include<stack> #include<deque> #include<cmath> #include<map> #define lson i<<1,l,mid #define rson i<<1|1,mid+1,r using namespace std; typedef long long ll; const int maxn=2e5+6; vector <int> son[maxn]; int fa[maxn][30]; int level[maxn]; bool used[maxn]; void dfs(int prev,int rt) { level[rt]=level[prev]+1; fa[rt][0]=prev; used[rt]=1; for(int i=1;i<25;i++) fa[rt][i]=fa[fa[rt][i-1]][i-1]; if(!son[rt].empty()) for(int i=0;i<son[rt].size();i++) { int s=son[rt][i]; if(!used[s]) dfs(rt,s); } } int lca(int x,int y) { if(level[x]<level[y]) swap(x,y); for(int i=24;i>=0;i--) { if(level[x]-(1<<i)>=level[y]) x=fa[x][i]; } if(x==y) return x; for(int i=24;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } bool cmp(int a,int b) { return level[a]>level[b]; } int main() { int n,m; cin>>n>>m; for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); son[x].push_back(y); son[y].push_back(x); } level[0]=-1; dfs(0,1); for(int i=0;i<m;i++) { int N; cin>>N; int v[N+6]; for(int i=0;i<N;i++) { scanf("%d",&v[i]); } sort(v,v+N,cmp); bool over=0; for(int i=1;i<N;i++) { //printf("%d-%d-=-=lca:%d\n",v[0],v[i],lca(v[0],v[i])); if(abs(level[lca(v[0],v[i])]-level[v[i]])>1) over=1; } if(over) printf("NO\n"); else printf("YES\n"); } return 0; }
Codeforces Round #629 (Div. 3) E. Tree Queries(lca题)
原文:https://www.cnblogs.com/studyshare777/p/12589529.html