最小生成树算法：Prim 算法

连通图：无向图G中，若从顶点i到顶点j有路径相连，则称i,j是连通的；如果G是有向图，那么连接i和j的路径中所有的边都必须同向；如果图中任意两点之间都是连通的，那么图被称作连通图。

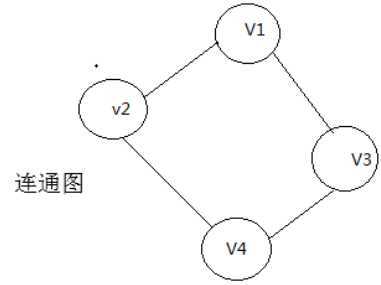
强连通图：有向图G中，对于任意的两个点之间x,y，都存在x到y的路径，为强连通图；

弱连通图：将有向图的所有的有向边替换为无向边，所得到的图称为原图的基图。如果一个有向图的基图是连通图，则有向图是若连通图；

单向连通：G=V,E;是有向图，对于任意u,v属于V，从u到达v或者v可达u,则称G为单向连通图；

连通分量：无向图的一个极大连通图子图称为G的一个连通分量；连通图只有一个连通分量；

极大连通子图：（无向图）

• 连通图只有一个极大连通子图，就是它本身；
• 非连通图有多个极大连通子图（非连通图的极大连通子图叫做连通分量，每个分量都是一个连通图）；
• 极大连通子图中，加入任何一个不在图点集中的点都会导致它不再连通；
• 下图为非连通图，图中有两个极大连通子图（连通分量）：

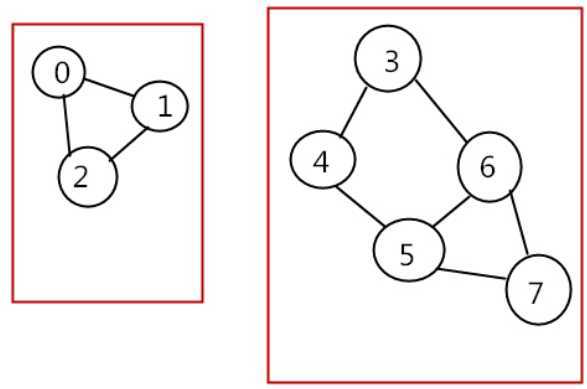
极小连通子图：（无向图）

• 一个连通图的生成树是该连通图的极小连通子图；（同一个连通图有不同的生成树，所以生成树不是唯一的，最小生成树是唯一的）；
• 极小连通子图是个连通图；
• 极小连通子图中，顶点个数为n, 则边的个数为n-1;
• 如果在生成树上添加一条边，一定会构成一个环；
• 极小连通子图的每条边都不可少，如果去掉一条边，则变成两个连通分量；
• 生成树：一个连通图的最小连通子图，无回路；

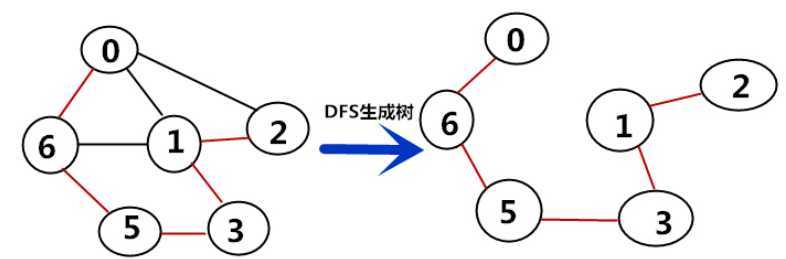
极大强连通子图：（有向图）

• 强连接图的极大强链接图为其本身；唯一；
• 非强连接图有多个极大强连通子图。非强连通图的极大连通子图叫做强连通分量；

最小生成树：一个有n个节点的连通图的生成树是原图的极小连通子图，且包含了原图中的所有n个节点，并且有保持图连通的最少的边；最少生成树可以使用Kruskal算法和Prim算法求出；

算法实现参考：https://github.com/yaowenxu/codes/tree/master/最小生成树算法

保持更新，转载请注明出处；更多内容请关注cnblogs.com/xuyaowen;

参考链接：

https://www.cnblogs.com/zhchoutai/p/8687614.html

极大连通子图与极小连通子图

最小生成树算法：Prim 算法

原文：https://www.cnblogs.com/xuyaowen/p/minimum-spanning-tree.html