前言

每每遇到关于排序算法的问题总是不能很好的解决，对一些概念，思想以及具体实现的认识也是模棱两可。归根结底，还是掌握不够熟练。以前只是看别人写，看了就忘。现在打算自己写，写些自己的东西，做个总结。本篇是这个总结的开始，所以我们先来阐述一下本次总结中会用到的一些概念。
排序是如何分类的？可以从不同的的角度对排序进行分类，这里我是根据排序的策略对本次总结中涉及到的排序算法进行分类：

说明

• 排序还会涉及到一个概念，叫排序的稳定性。那么稳定性是什么意思呢？
  稳定性，就是有两个相同的元素，排序后它们相对位置是否发生变化，若未变化则该称该排序算法是稳定的。否则就是不稳定的。
• 本次总结所有的算法实现均是以从小到大为例进行排序的，后面不再特别指出。
• 文章后面将会提到的有序区，无序区。是指在待排序列中，已经排好顺序的元素，就认为其是处于有序区中，还没有被排序的元素就处于无序区中。
• 小提示，点击文章页面右下角的“查看目录”可以查看本文目录哦

接下来，我们开始进入正文

交换排序

交换排序主要包括两种排序算法，分别是冒泡排序和快速排序

冒泡排序

基本思想

从后往前，两两比较待排序列中的元素的大小，若比较结果不符合要求，则进行交换。这样较小的元素会一直向前移动
通过无序区中相邻元素的比较和交换，使最小的元素如气泡一般逐渐往上漂浮至水面

复杂度与稳定性与优缺点

• 空间复杂度：O(1)
• 时间复杂度：O(n²)
• 最好情况：正序有序时，普通冒泡排序仍是O(n^2)，优化后的冒泡排序是O(n)
• 最坏情况：逆序有序时，O(n²)
• 稳定性：稳定
• 优点：简单，稳定，空间复杂度低
• 缺点：时间复杂度高，效率不好，每次只能移动相邻两个元素，比较次数多

算法实现

public void BubbleSort(int[] array){
    for(int i = 0; i < array.Length - 1; i ++){
        for(int j = array.Length - 1; j > i ; j --){
            if(array[j] < array[j - 1]){
                Swap(array, j, j - 1);
            }
        }
    }
}

// 实现将指定下标的两个元素在数组中交换位置
public void Swap(int[] array, int i, int j){
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

【算法解读】

算法的外层循环中的i可以理解为有序区的边界，从0开始即表示初始时有序区是空的。当外层循环执行完一次后，会有一个无序区中最小的元素移动到有序区中，此时i + 1 = 1表示有序区边界扩大了，i以内的元素都处在有序区中。当i = array.Length - 1时，即表示所有元素都处于有序区了，算法结束。
内层循环负责将无序区中的最小元素移动到有序区中，依次对无序区中相邻元素进行比较，如果位置靠后的元素小于位置靠前的元素，则交换两个元素。如此一来，无序区中最小的元素就会被一步步交换到有序区的末尾。

【举个栗子】

对于待排序列4,1,3,2
首先依次比较无序区（初始时为所有元素）中的相邻元素，比较3,2，位置靠后的元素小于位置靠前的元素，则交换。序列为4,1,2,3。继续比较1,2，位置靠后的元素大于位置靠前的元素，不交换。继续比较4,1，需要交换，此时无序区中的元素全部比较完毕，一趟冒泡排序结束，序列为1,4,2,3。可以看到最小元素1已经移动到序列首部，即处于有序区内，确定了一个元素的位置。无序区还剩下4,2,3。重复上述操作完成最终排序。

冒泡排序优化

当待排序列是正序有序时，冒泡排序的时间复杂度仍然是O(n²)，针对这点我们可以做一些优化
当内层循环执行完成一趟却没有发生交换时，说明此时的待排序列已经是正序有序的了，可以直接终止算法。

public void BubbleSortOptimize(int[] array){
    for(int i = 0; i < array.Length - 1; i ++){
        bool swapTag = false; // 标志位，判断每完成一趟冒牌排序是否发生交换
        for(int j = array.Length - 1; j > i; j --){
            if(array[j] < array[j - 1]){
                Swap(array, j, j -1);
                swapTag = true;
            }
        }
        if(!swapTag){
            break;
        }
    }
}

快速排序

基本思想

快速排序又被称为分区交换排序，是目前已知的平均速度最快的一种排序方法，它采用了一种分治的策略，是对冒泡排序的一种改进。
在待排序列中任取其中一个元素作为目标元素（称其为枢轴或分界点），以该元素为分界点（pivot）进行分区，将待排序列分成两个部分，所有比分界点小的元素都放置于分界点左边，所有比分界点大的元素都放置于分界点的右边，然后再分别将左右两边作为两个待排序列，重复上述过程，直到每个分区只剩下一个元素为止。显然，每一趟快速排序后，分界点都找到了自己在有序序列中的位置

复杂度与稳定性与优缺点

• 空间复杂度：O(log₂ⁿ)取决于递归深度，所占用的栈空间
• 时间复杂度：O(nlog₂ⁿ)
• 最好情况：O(nlog₂ⁿ)，当每次分区，分界点左，右两边的分组长度大致相等时，快速排序算法的性能最好
• 最坏情况：O(n²)，当每次选择的分界点都是当前分组的最大元素或最小元素时，快速排序算法退化为冒泡算法。
• 稳定性：不稳定，因为将元素移动到分界点两边时，会打乱原本相等元素的顺序
• 优点：极快
• 缺点：不稳定

算法实现

public void QuickSort(int[] array){
    QuickSortImpl(array, 0, array.Length - 1);
}

public void QuickSortImpl(int[] array, int left, int right){
    if(left >= right) return;
    int pivot = Partition(array, left, right);
    QuickSortImpl(array, left, pivot - 1);
    QuickSortImpl(array, pivot + 1, right);
}

// 分区函数，实现将所有元素依据大小移动到分界点的两边
public int Partition(int[] array, int left, int right){
    int target = array[left];
    while(left < right){
        while(right > left && array[right] >= target){
            right --;
        }
        if(right > left){
            array[left] = array[right];
            // 此时left位置的元素是被移动过来的元素，肯定比目标元素小
            // 所以左指针扫描时就可以不用比较该元素，进行left++操作
            left ++; 
        }
        while(left < right && array[left] <= target){
            left ++;
        }
        if(left < right){
            array[right] = array[left];
            right --;
        }
    }
    array[left] = target;
    return left;
}

【算法解读】

算法首先选取待排序列的首元素作为分界点，调用Partition方法进行分区，将待排序列依据分界点分成两个部分。每个子部分再作为待排序列进行递归调用。直到每部分只剩一个元素（对应代码：if(left >= right) return;）。
算法的关键在于Partition方法内部，通过左右指针不断进行比较替换。首先准备移动右指针（因为当找到比分界点小的元素时，可以先将其移动到左指针指向的位置，而左指针所指向位置的元素已经被保存到target中，不用担心被覆盖），找到比分界点小的元素后将其移动到左指针指向的位置。右指针停止。准备移动左指针，找到比目标元素大的元素后，将其移动到右指针指向的位置（此时原来在右指针位置的元素也已经被移动走了，可以直接覆盖），左指针停止。再次开始移动右指针，重复上述操作。直到左指针和右指针重合，它们指向的位置就是分界点元素应该在的最终位置。

【举个栗子】

对于待排序列3,1,4,2
先看图：

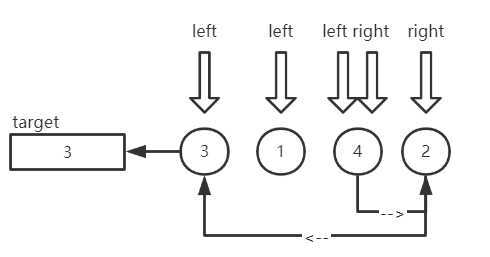
首先选取首元素3作为目标元素，并将其保存在临时变量target中。起始left指向3，right指向2。开始移动右指针，发现2比目标元素3小，则将2移动到left指向的位置，注意此时left向右移动一位，指向1。右指针停止。开始移动左指针，1比3小符合要求，继续移动，发现4比3大，不符合要求，将4移动到right位置（即原来2的位置，同理right也左移一位），left指针停止。
重新准备移动右指针，发现right与left重合则第一次分区结束。3找到了它的最终位置，即left，right重合的位置，将3移动到该位置。此时序列为2,1,3,4。
继续递归重复上述操作。

快速排序优化策略

这里简单介绍一下快速排序可以做的一些优化

• 当待排序列是部分有序时，固定选取枢轴（即分界点）会使快排效率低下，要缓解这种情况，可以引入随机选取枢轴的方式
• 当待排序列长度分割到一定大小后，可以使用插入排序代替快速排序，因为对于很小和部分有序的序列，简单插入排序的效率更好
• 针对递归的优化，算法中调用了两次QuickSortImpl进行递归，其实第二次调用可以使用循环代替，即改为 left = pivot + 1

插入排序

插入排序主要包括两种排序算法，分别是简单插入排序和和希尔排序

简单插入排序

基本思想

每次将一个无序区的元素，按其大小找到其在有序区中的位置，并插入到该位置，直到全部元素插完为止。
插入排序不是通过交换位置而是通过比较找到合适的位置插入元素来达到排序的目的

复杂度与稳定性与优缺点

• 空间复杂度：O(1)
• 时间复杂度：O(n²)
• 最好情况：O(n)，正序有序时
• 最坏情况：O(n²)，逆序有序时
• 稳定性：稳定
• 优点：稳定，快，如果序列是基本有序的，使用直接插入排序效率就非常高
• 缺点：插入次数不一定，插入越多，插入点后的数据移动越多，特别是数据量庞大的时候，但用链表可以 解决这个问题。

算法实现

public void SimpleInsertionSort(int[] array){
    for(int i = 1; i < array.Length; i ++){
        int j = i;
        int target = array[j];
        while(j > 0 && target < array[j - 1]){
            array[j] = array[j - 1];
            j --;
        }
        array[j] = target;
    }
}

【算法解读】

算法默认待排序列的第一个元素是排好序的，处于有序区。从第二个元素开始，直到到末尾元素，依次作为目标元素（对应代码：for(int i = 1; i < array.Length; i ++))，向有序区中插入。那么如何插入呢？将目标元素依次和有序区的元素进行比较，若目标元素小于该元素，则目标元素就应处于该元素的前面，则该元素后移一个位置(对应代码：array[j] = array[j - 1];)。不断比较直到找到不比目标元素小的元素，则目标元素就应在该元素的后面位置，将目标元素插入到该位置。继续下一个目标元素，直到所有元素插入完毕。
在开始插入第i个元素时，前i-1个元素已经是排好序的。

【举个栗子】

对于待排序列3,1,4,2
首先认为3是有序的，处于有序区。将1作为目标元素，依次和有序区中的元素进行比较，和3进行比较，1<3，则3后移，有序区中没有待比较的数据了，所以将1插入到3原来的位置。此时序列：1,3,4,2。有序区内元素为1,3。继续将4作为目标元素，先和3比较，4>3，则插入到4的后面位置。此时序列1,3,4,2。此时有序区内元素为1,3,4。继续将2作为目标元素，和4比较，2<4，4后移，和3比较，2<3，3后移，和1比较，2>1，则插入到1的后面。此时序列1,2,3,4。所有元素插入完毕，即排序完成。

希尔排序

基本思想

希尔排序是插入排序的一种高效率的实现，又称缩小增量式插入排序。它也是简单插入排序算法的一种改进算法。
先选定一个数作为第一个增量，将整个待排序列分割成若干个组，分组方式是将所有间隔为增量值的元素放在同一个组内。各组内部进行直接插入排序。然后缩小增量值，重复上述分组和排序操作，直到所取增量减少为1时，即所有元素放在同一个组中进行直接插入排序。

为什么希尔排序的时间性能是优于简单插入排序的呢？
开始时，增量较大，每组中的元素少，因此组内的直接插入排序较快，当增量减少时，分组内的元素增加，但此时分组内的元素基本有序，所以使得组内的直接插入排序也较快，因此，希尔排序在效率上较简单插入排序有较大的改进

复杂度与稳定性与优缺点

• 空间复杂度：O(1)
• 时间复杂度：O(nlog₂ⁿ)
• 最好情况：O(nlog₂ⁿ)，因为希尔排序的执行时间依赖于增量序列，如何选择增量序列使得希尔排序的元素比较次数和移动次数较少，这个问题目前还未能解决。但有实验表明，当n较大时，比较和移动次数约在 n^1.25~1.6n1.25。
• 最坏情况：O(nlog₂ⁿ)
• 稳定性：不稳定，相同元素可能分在不同的组内，导致顺序可能发生改变
• 优点：快，数据移动少
• 缺点：不稳定，d的取值是多少，应该取多少个不同的值，都无法确切知道，只能凭经验来取

算法实现

public void ShellSort(int[] array){
    int d = array.Length / 2;
    while(d >= 1){
        for(int i = d; i < array.Length; i ++){
            int j = i;
            int target = array[j];
            while(j >= d && target < array[j -d]){
                array[j] = array[j - d];
                j -= d;
            }
            array[j] = target;
        }
        d /= 2;
    }
}

【算法解读】

希尔排序算法是对简单插入排序的改进，所以如果对简单插入排序还不够理解的话，建议先去看一下上面的简单插入排序算法。
算法首先取增量为待排序列长度的一半，通过增量进行分组，每个分组都进行简单插入排序。然后，增量减半，重复上述操作直至增量减少为1（对应代码：while(d >= 1)）。
算法的要点在于对每个分组进行简单插入排序。首先从i = d位置上的元素开始，一直到待排序列的最后一个元素，依次作为目标元素，找到它们应该在自己分组中的位置并进行插入。当目标元素位置为i时，则目标元素所在分组的有序区内的元素位置分别为i-d，i-d-d，i-d-d-d...直到该位置大于0。目标元素只需要和所在分组有序区内的元素进行比较，找到自己的最终位置即可。当增量减少为1时，则相当于只有一个分组，此时就是对所有元素进行直接插入排序，完成最终的希尔排序。

【举个栗子】

对于待排序列4,1,3,2
先看图：

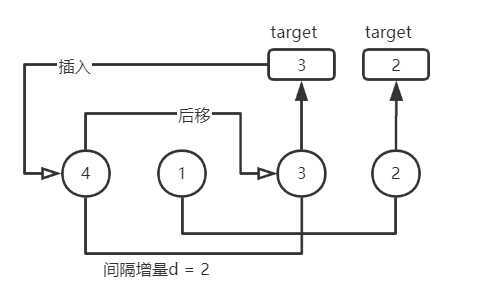
首先取增量为序列长度4的一半，即为2。此时的分组是（4,3），（1,2）。则从下标为2的元素3开始作为目标元素，下标2减去增量2，则找到目标元素3所在分组有序区内的元素4，和4进行比较，3<4，则4后移（这里的后移都是相对于自己所在分组里的元素），有序区内没有其它元素，则目标元素3插入到元素4之前的位置。此时序列为3,1,4,2。继续从下标为3的元素2开始作为目标元素，找到目标元素2所在分组有序区内的元素1，比较2>1，符合预期都不需要移动。一趟希尔排序完成，序列仍为3,1,4,2。增量再减半为1，此时就是对所有元素进行简单插入排序，不再赘述。

希尔排序的关键点在于分组，我们再举个栗子看是如何分组的：
对于序列25,36,48,59,13,21,74,32,60
第一次增量为序列长度9的一半，取下限是4，此时的分组情况是（25,13,60）（36,21）（48,74）（59,32），如下图：

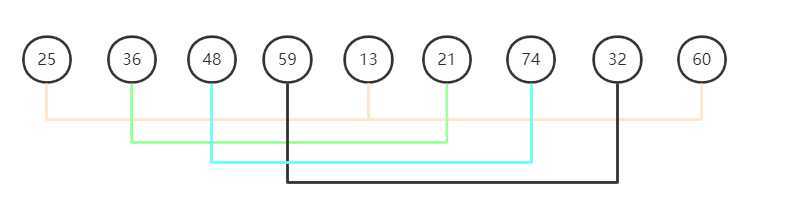
那么到这里，交换排序中的冒泡排序，快速排序和插入排序中的简单插入排序，希尔排序，就总结完了。
后面我会继续总结选择排序中的简单选择排序算法，堆排序算法，以及归并，基数，计数排序算法，敬请期待。

上面算法的源码都放在了GitHub上，感兴趣的同学可以点击这里查看
更多算法的总结与代码实现（不仅仅是排序算法），欢迎大家查看我的GitHub仓库Algorithm

常见排序算法总结与分析之交换排序与插入排序-C#实现

原文：https://www.cnblogs.com/iwiniwin/p/12589405.html