【深度学习】perceptron（感知机）

个人学习笔记，有兴趣的朋友可参考。

1.感知机的描述

感知机（perceptron）由美国学者Frank Rosenblatt在1957年提出来的。是作为神经网络（深度学习）的起源的算法、
学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想

感知机接收多个输入信号，输出一个信号。如下图:

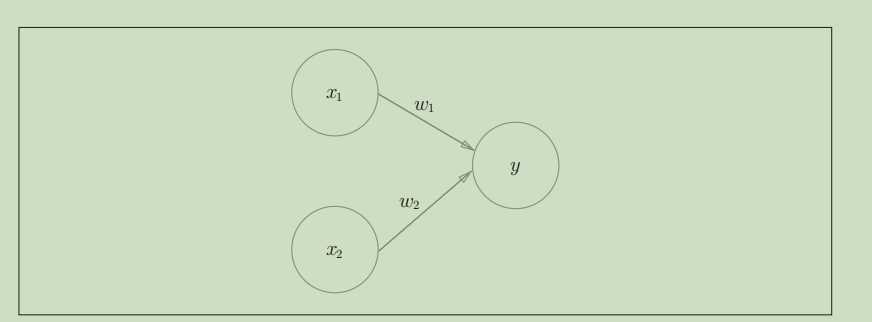
其中:

• x1、x2是输入信号,y是输出信号
• w1、w2是权重
• 图中的○,代表一个个“神经元”
• 通过一个固定的权重算法（w1x1、w2x2）,当超过θ这个阈值，输出1，代表“神经元被激活”。否则为0，代表未激活、

公式如下:

2.感知机解决简单逻辑电路，与门的问题。

与门的真值表如下:

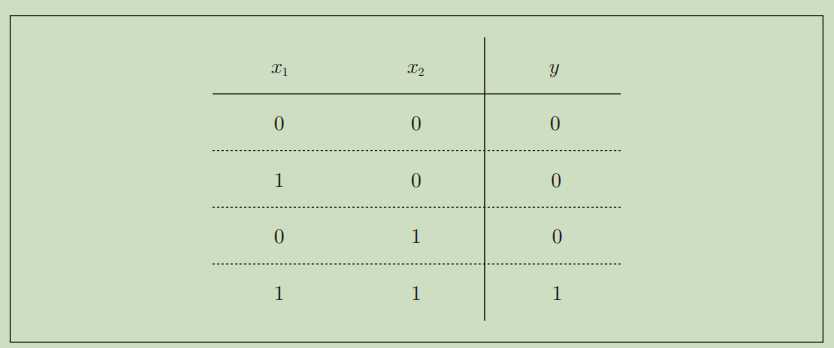
就是两个输入都为1的情况下，输出才为1。

代码如下:

def AND(x1,x2):
    w1,w2,theta =0.5,0.5,0.6
    tmp =x1*w1 +x2*w2
    if tmp <= theta:
        return 0
    elif tmp >theta:
        return 1

print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))

演示效果如下:

(zsdpy1) zsd@zsd-virtual-machine:~/ZAI$ python section04.py 
0
0
0
1

2.多层感应机，解决异或门

异或门的真值表

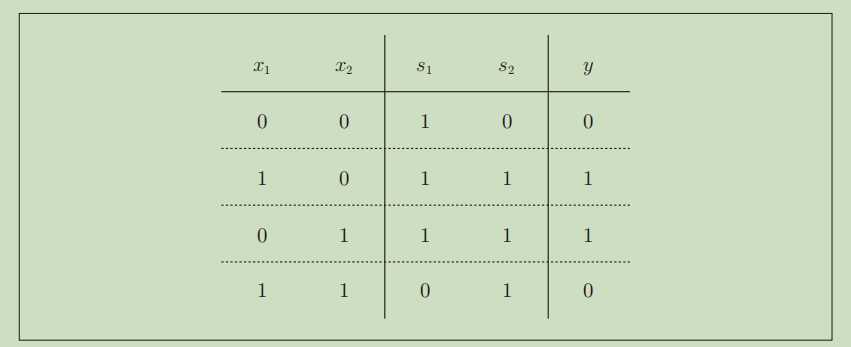
可以看到，异或门用一层没有办法解决。所以我们可以再来一个"叠加层"、通过多层的结构。来达到异或门的效果。

如下图:

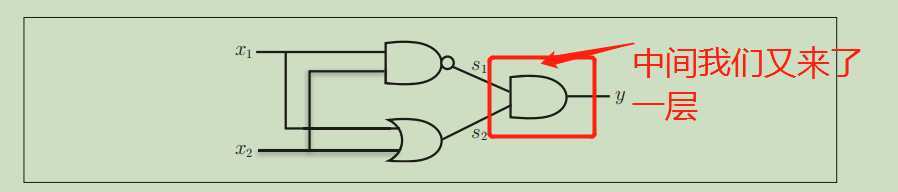
代码的实现，可能需要把与门，非门，与非门的函数都实现一遍。通过它们的组合完成异或门(大学时期学的逻辑电路终于派上了一点点用场了)

代码如下:

import numpy as np

def AND(x1,x2):
    w1,w2,theta =0.5,0.5,0.6
    tmp =x1*w1 +x2*w2
    if tmp <= theta:
        return 0
    elif tmp >theta:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1


def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y


if __name__ == ‘__main__‘:
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

演示效果如下:

(zsdpy1) zsd@zsd-virtual-machine:~/ZAI$ python section05.py 
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

【深度学习】perceptron（感知机）

原文：https://www.cnblogs.com/zhangshengdong/p/12613674.html