Input
Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
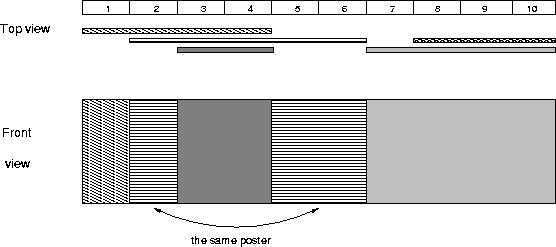
题意:每次从给定的位置a到b粘贴报纸,这次的可以覆盖上次的,问n次之后还能看见多少种。
思路:(在做这题之前最好先去了解一下线段树的染色问题,这里就不在赘述了)
区间修改问题,自然想到要用线段树,但看一下数据范围 10000000需要离散化一下。这题的离散化还有点小特殊,具体看下面的解释
例如先后覆盖 [1,10] [1,4] [6,10] 答案应该是 3
把这下节点都取下来 1 10 1 4 6 10;
排序去重 1 4 6 10;
重新映射
1 4 6 10
1 2 3 4;
离散化后的 [1,4] [1,2] [3,4] 。
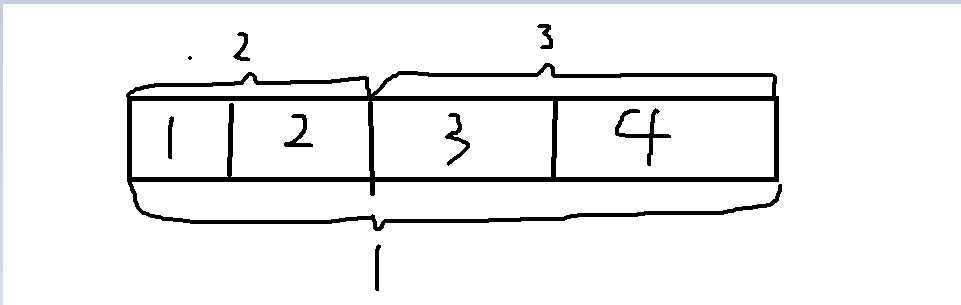
可以看到第一次[1 4],第二次[1 2], 第三次[3 4],这样把[1 4]全盖死了,答案是2所以需要进行一下小优化
我们离散的时候来个判断,如果相邻数字间距大于1的话,就在其中加上任意一个数字,比如加成[1,3,4,5,6,7,10],这样的话离散就成功了;
具体看代码
for(int i=1; i<=n; i++) { scanf("%d%d",&le[i],&ri[i]); num[cnt++]=le[i]; num[cnt++]=ri[i]; } sort(num,num+cnt);//排序 tmp=cnt=unique(num,num+cnt)-num;//去重 for(int i=1; i<tmp; i++) { if(num[i]-num[i-1]>1) num[cnt++]=num[i-1]+1; }//+1
代码:
#include <iostream> #include <string.h> #include <string> #include<cstdio> #include <algorithm> #include<map> #define ll long long using namespace std; int ans=0,cnt=0; map<int,int>q; ll tree[800010]; void push_up(ll rt) { if( tree[rt*2+1]==tree[rt*2+2]) { tree[rt] = tree[rt*2+1]; } else tree[rt]=0; } void push_down(ll rt) //lazy的方法,本题比较特殊需要用tree数组代替add数据就行 { if(tree[rt]) { tree[rt*2+1]=tree[rt]; tree[rt*2+2]=tree[rt]; tree[rt] = 0; } } //板子直接套(注意该树是从节点0开始的) void bulid_tree(int node,int start,int end) { if(start==end) { tree[node]=0; } else { ll mid=(start+end)/2; ll left_node=2*node+1; ll right_node=2*node+2; bulid_tree(left_node,start,mid); bulid_tree(right_node,mid+1,end); } } //建树,递归的方法; void update_tree(int L, int R, ll key, int l, int r, int rt) //区间更新 L,R要查询的区间 { // cout<<"L="<<L<<" "<<"R="<<R<<" "<<l<<" "<<r<<endl; if(L<=l&&r<=R) { tree[rt]=key; //key 代表第几种报纸 return; } push_down(rt);//向下更新 ll mid=(l+r)/2; ll left_node=2*rt+1; ll right_node=2*rt+2; if(L <= mid) update_tree(L, R, key,l,mid,left_node); if(R > mid) update_tree(L, R, key,mid+1,r,right_node); push_up(rt);//向上更新 } void query_tree(int l, int r, int rt) { if(l==r&&!tree[rt]) return; if(tree[rt]) { if(q[tree[rt]]==0) //当节点不为0的时候代表在这个节点上有报纸,需要进项统计,在判断是否是第一次出现,如果是第一次出现就ans++. { ans++; q[tree[rt]]=1; } return; } // push_down(rt); ll mid=(l+r)/2; ll left_node=2*rt+1; ll right_node=2*rt+2; query_tree(l,mid,left_node); query_tree(mid+1,r,right_node); } int main() { int t; cin>>t; while(t--) { int le[10005],ri[10005],num[40005],cnt,tmp,n; q.clear(); cnt=ans=0; cin>>n; for(int i=1; i<=n; i++) { scanf("%d%d",&le[i],&ri[i]); num[cnt++]=le[i]; num[cnt++]=ri[i]; } sort(num,num+cnt); tmp=cnt=unique(num,num+cnt)-num; for(int i=1; i<tmp; i++) { if(num[i]-num[i-1]>1) num[cnt++]=num[i-1]+1; } sort(num,num+cnt); /*for(int i=0; i<cnt; i++) { cout<<num[i]<<" "; }*/ bulid_tree(0,0,cnt-1); for(int i=1; i<=n; i++) { int s=lower_bound(num,num+cnt,le[i])-num; int k=lower_bound(num,num+cnt,ri[i])-num; /*cout<<le[i]<<"**********************************"<<ri[i]<<endl; cout<<s<<"*********"<<k<<endl;*/ update_tree(s,k,i,0,cnt-1,0); } query_tree(0,cnt-1,0); cout<<ans<<endl; } }
最后离散化的代码我在单独放出来
for(int i=1; i<=n; i++) { scanf("%d%d",&le[i],&ri[i]); num[cnt++]=le[i]; num[cnt++]=ri[i]; } sort(num,num+cnt); tmp=cnt=unique(num,num+cnt)-num;//去重 for(int i=1; i<tmp; i++) { if(num[i]-num[i-1]>1) num[cnt++]=num[i-1]+1; } sort(num,num+cnt); /*for(int i=0; i<cnt; i++) { cout<<num[i]<<" "; }*/ bulid_tree(0,0,cnt-1); for(int i=1; i<=n; i++) { int s=lower_bound(num,num+cnt,le[i])-num; //建立左端点新的映射关系 int k=lower_bound(num,num+cnt,ri[i])-num; //建立右端点新的映射关系 update_tree(s,k,i,0,cnt-1,0); //用新的映射关系进想区间修改 }
原文:https://www.cnblogs.com/sszywq/p/12613652.html