在本程序中默认该现行规划问题有最优解
针对此问题:
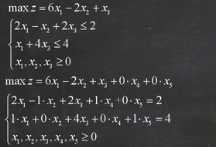
1 #include<iostream> 2 using namespace std; 3 4 int check(float *sigema, int m) { 5 for (int i = 1; i <= m ; i++) { 6 if (sigema[i] > 0) { 7 return 0; 8 } 9 } 10 return 1; 11 } 12 13 //此程序已经化为标准型的线性规划问题中,且默认有最优解 14 int main(int argc, char* argv[]) 15 { 16 //数据输入部分 17 int m, n; 18 cout << "请输入变量个数:"; 19 cin >> m; 20 cout << "请输入不等式个数:"; 21 cin >> n; 22 float **matrix = new float*[n + 1]; //系数矩阵 23 for (int i = 1; i <= n; i++) { 24 matrix[i] = new float[m + 2]; 25 } 26 float *cj = new float[m + 1]; 27 float *cB = new float[n + 1]; //基变量系数 28 int *XB = new int[n + 1]; //用来标注基变量x的下标 29 float *b = new float[n + 1]; 30 float *sigema = new float[n + 1]; 31 float *sita = new float[n + 1]; 32 //初始化 33 for (int i = 0; i <= m; i++) { 34 cj[i] = 0; 35 } 36 for (int i = 0; i <= n; i++) { 37 cB[i] = 0; 38 XB[i] = 0; 39 b[i] = 0; 40 sigema[i] = 0; 41 sita[i] = 0; 42 } 43 cout << "请输入目标函数系数(用空格间开):" << endl; 44 for (int i = 1; i <= m; i++) { 45 cin >> cj[i]; 46 } 47 cout << "请输入各不等式的系数和常量(用空格间开):" << endl; 48 for (int i = 1; i <= n; i++) { 49 cout << "不等式" << i << ": "; 50 for (int j = 1; j <= m + 1; j++) { 51 cin >> matrix[i][j]; 52 } 53 } 54 cout << "请输入目标函数中基变量下标:" << endl; 55 for (int i = 1; i <= n; i++) { 56 cin >> XB[i]; 57 cB[i] = cj[XB[i]]; 58 //常量 59 b[i] = matrix[i][m + 1]; 60 } 61 62 //计算检验数 63 for (int i = 1; i <= m; i++) { 64 sigema[i] = cj[i]; 65 for (int j = 1; j <= n; j++) { 66 sigema[i] -= cB[j] * matrix[j][i]; 67 } 68 } 69 70 while (check(sigema, m) == 0) { 71 //寻找入基变量 72 float maxn = sigema[1]; 73 int sigema_xindex = 0; 74 float sigema_xcoefficient = 0; 75 for (int i = 1; i <= m; i++) { 76 if (maxn <= sigema[i]) { 77 maxn = sigema[i]; 78 sigema_xindex = i; 79 sigema_xcoefficient = cj[i]; 80 } 81 } 82 //计算sita 83 for (int i = 1; i <= n; i++) { 84 if (matrix[i][sigema_xindex] > 0) { 85 sita[i] = b[i] / matrix[i][sigema_xindex]; 86 } 87 else { 88 sita[i] = 9999; //表示sita值为负数 89 } 90 } 91 //寻找出基变量 92 float minn = sita[1]; 93 int sita_xindex = 0; 94 for (int i = 1; i <= n; i++) { 95 if (minn >= sita[i] && sita[i] > 0) { 96 minn = sita[i]; 97 sita_xindex = i; 98 } 99 } 100 //入基出基变换,先入基再出基 101 //入基操作 102 for (int i = 1; i <= n; i++) { 103 if (i == sita_xindex) { 104 XB[i] = sigema_xindex; 105 cB[i] = sigema_xcoefficient; 106 break; 107 } 108 } 109 //出基计算 110 //化1 111 //cout << endl << "此处为化1的结果------" << endl; 112 float mul1 = matrix[sita_xindex][sigema_xindex]; 113 for (int i = 1; i <= m; i++) { 114 matrix[sita_xindex][i] /= mul1; 115 } 116 b[sita_xindex] /= mul1; 117 //化0 118 //cout << endl << "此处为化0的结果------" << endl; 119 for (int i = 1; i <= n; i++) { 120 if (i == sita_xindex) { 121 continue; 122 } 123 float mul2 = matrix[i][sigema_xindex] / matrix[sita_xindex][sigema_xindex]; 124 for (int j = 1; j <= m; j++) { 125 matrix[i][j] -= (matrix[sita_xindex][j] * mul2); 126 } 127 b[i] -= (b[sita_xindex] * mul2); 128 } 129 for (int i = 1; i <= n; i++) { 130 if (i == sita_xindex) { 131 continue; 132 } 133 } 134 for (int i = 1; i <= m; i++) { 135 sigema[i] = cj[i]; 136 for (int j = 1; j <= n; j++) { 137 sigema[i] -= cB[j] * matrix[j][i]; 138 } 139 } 140 } 141 float MaxZ = 0; 142 float *result = new float[m + 1]; 143 for (int i = 0; i <= m; i++) { 144 result[i] = 0; 145 } 146 for (int i = 1; i <= n; i++) { 147 result[XB[i]] = b[i]; 148 } 149 cout << "最优解为:X = ("; 150 for (int i = 1; i < m; i++) { 151 cout << result[i] << ","; 152 } 153 cout << result[m] << ")" << endl; 154 for (int i = 1; i <= m; i++) { 155 MaxZ += result[i] * cj[i]; 156 } 157 cout << "最优值为:MzxZ = " << MaxZ; 158 return 0; 159 }
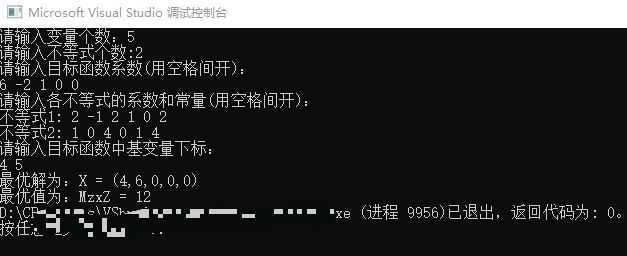
程序运行结果:
原文:https://www.cnblogs.com/zz-1120-wtenlb/p/12616481.html