62 方块转换
作者:
问题描述 :
一块N x N(1=<N<=10)正方形的黑白瓦片的图案要被转换成新的正方形图案。
写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式:
#1:转90度:图案按顺时针转90度。
#2:转180度:图案按顺时针转180度。
#3:转270度:图案按顺时针转270度。
#4:反射:图案在水平方向翻转(形成原图案的镜像)。
#5:组合:图案在水平方向翻转,然后按照#1-#3之一转换。
#6:不改变:原图案不改变。
#7:无效转换:无法用以上方法得到新图案。
如果有多种可用的转换方法,请选择序号最小的那个。
比如:
转换前:
@-@
---
@@-
转换后:
@-@
@--
--@
这种转换采取#1(按顺时针转90度)即可。
注意:图案中的字符“@”和“-”在转90度后,还是“@”和“-”。不要认为“-”转90度后变成“|”。
输入说明 :
第一行: 单独的一个整数N。
第二行到第N+1行: N行,每行N个字符(不是‘@‘就是‘-‘);这是转换前的正方形。
第N+2行到第2*N+1行: N行,每行N个字符(不是‘@‘就是‘-‘);这是转换后的正方形。
输出说明 :
单独的一行包括1到7之间的一个数字(在上文已描述)表明需要将转换前的正方形变为转换后的正方形的转换方法。
输入范例 :
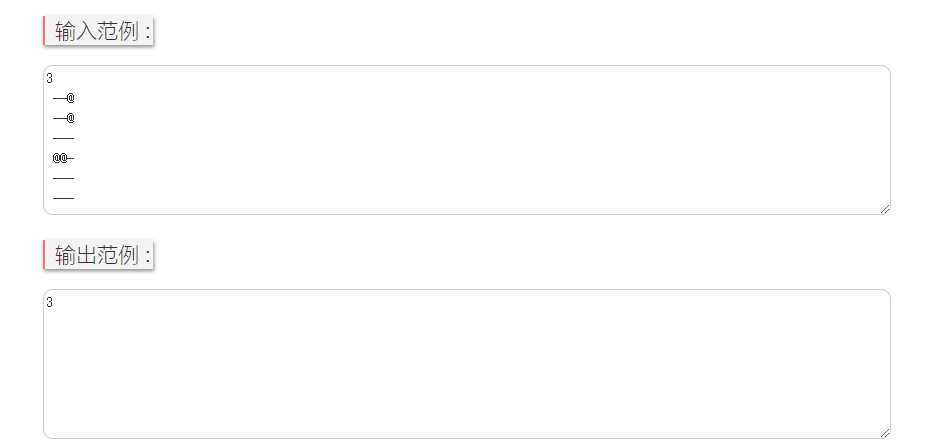
解题思路:这道题目稍微复杂一些,思路并不难。主要是矩阵旋转比较新颖,不过细细观察后会发现有数学规律,有了规律一切就好办了。
例如旋转90度后,矩阵之间的关系是这样的。
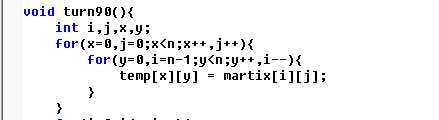
依照这个思路,我们可以模拟题目的过程,如果符合某种情况,输出该情况的数字即可。
不过在实际操作中遇到了一点问题。
1、输入字符异常
一开始仅仅采用scanf("%c",&ch);处理,后来想到可能有多余的回车字符。加入getchar()处理,但是输入依然不正常,仔细看看样例发现每行之前还有一个空格
再加一个getchar();处理OK了
完整代码
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <math.h> 4 #include <string.h> 5 #include <ctype.h> 6 7 8 #define maxn 15 9 10 11 12 char martix1[maxn][maxn];//原来的矩阵 13 char martix[maxn][maxn];//暂存矩阵(上次的) 14 char martix2[maxn][maxn]; 15 char temp[maxn][maxn]; //用于与结果比较的矩阵 16 17 18 int n; 19 int flag; 20 21 int convert(); 22 void initTemp(); 23 int compare(); 24 void turn90(); 25 void mirro(); 26 int main(){ 27 28 int i,j; 29 scanf("%d",&n); 30 char num; 31 for(i=0;i<n;i++){ 32 getchar(); 33 getchar(); 34 for(j=0;j<n;j++){ 35 scanf("%c",&num); 36 martix1[i][j] = num; 37 martix[i][j] = num; //暂存矩阵 38 } 39 } 40 41 for(i=0;i<n;i++){ 42 getchar(); 43 getchar(); 44 for(j=0;j<n;j++){ 45 scanf("%c",&num); 46 martix2[i][j] = num; 47 } 48 } 49 50 51 flag = 0; 52 int id = convert(); 53 54 if(id < 8){ 55 if(id>=5){ 56 id = 5; 57 } 58 }else{ 59 if(flag == 1){ 60 id =6; 61 }else{ 62 id = 7; 63 } 64 } 65 66 printf("%d\n",id); 67 return 0; 68 } 69 70 71 int convert(){ 72 int id; 73 initTemp(); 74 if(compare()==1){ 75 flag = 1;//不变 76 } 77 id = 1; 78 turn90(); 79 80 if(compare()==1){ 81 return id; 82 } 83 id ++; 84 turn90(); 85 86 if(compare()==1){ 87 return id; 88 } 89 id ++; 90 turn90(); 91 92 if(compare()==1){ 93 return id; 94 } 95 id ++; 96 turn90();//补充一个 97 mirro(); 98 99 if(compare()==1){ 100 return id; 101 } 102 id ++;//5 103 turn90(); 104 105 if(compare()==1){ 106 return id; 107 } 108 id ++; 109 turn90(); 110 111 if(compare()==1){ 112 return id; 113 } 114 id ++; 115 turn90(); 116 117 if(compare()==1){ 118 return id; 119 } 120 id ++;//8 121 return id; 122 123 124 } 125 126 void initTemp(){ 127 int i,j; 128 for(i=0;i<n;i++){ 129 for(j=0;j<n;j++){ 130 temp[i][j] = martix1[i][j]; 131 } 132 } 133 } 134 135 136 int compare(){ 137 int i,j; 138 for(i=0;i<n;i++){ 139 for(j=0;j<n;j++){ 140 if(martix2[i][j]!=temp[i][j]){ 141 return 0; 142 } 143 } 144 } 145 return 1; 146 } 147 148 void turn90(){ 149 int i,j,x,y; 150 for(x=0,j=0;x<n;x++,j++){ 151 for(y=0,i=n-1;y<n;y++,i--){ 152 temp[x][y] = martix[i][j]; 153 } 154 } 155 for(i=0;i<n;i++){ 156 for(j=0;j<n;j++){ 157 martix[i][j] = temp[i][j];//记录暂存矩阵 158 } 159 } 160 } 161 162 void mirro(){ 163 int i,j; 164 for(i=0;i<n;i++){ 165 for(j=0;j<n/2;j++){ 166 int temp = martix[i][j]; 167 martix[i][j] = martix[i][n-1-j]; 168 martix[i][n-1-j] = temp; 169 } 170 } 171 for(i=0;i<n;i++){ 172 for(j=0;j<n;j++){ 173 temp[i][j] = martix[i][j];//记录暂存矩阵 174 } 175 } 176 }
原文:https://www.cnblogs.com/ManOK/p/12616424.html