【做题笔记】P1359租用游艇

不知为啥我觉得这是一道挺毒瘤的dp，，，可能是我太弱了。

那个半矩阵一开始我都不知道是啥。。。

感谢@do_while_true 以及 @qym2008 的回答:https://www.luogu.com.cn/discuss/show/207793

拿样例来说：

3
5 15
7

5为1行1数，表示1到2距离；
15为1行2数，表示1到3距离；
第 \(i\) 行第 \(j\) 个数表示 \(i\) 到点 \(j+1\) 的距离，不妨记为 \(x\) 。

然后这题之所以可以不用最短路算法做是因为，题目直接给出了整个图的信息，而我们又只需要求1~n的“最短路”。 所以我们设计一种 dp 算法即可。

注意到我们只关心最后的结果是多少，而不关心中间到底经过了哪些路线，所以记 \(f_j\) 为 1~j 的最小花费，那么有：

为什么能这么干呢？我们发现，1~j 的路径有很多条，假设我们现在有一条 1~i 的目前的最短路径，而现在又输入了 \(x\) 代表 i~j 的花费，那么最优解必定有可能被更新，因为 \(f_i\) 代表目前的 1~i 的最优花费，那么加上刚刚输入的那一条边，就有可能产生一条新的路径，使得花费更优。例如下图：

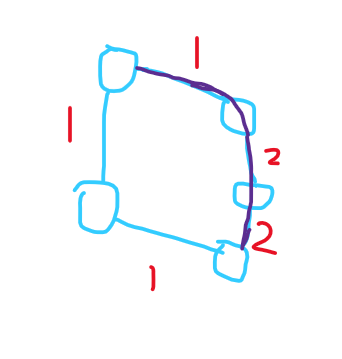
紫色的路径是我们以前找到的，那么假如又知道了左边的那条路径（\(f_i+x\)），最优值就被更新了！见下图绿色线路：

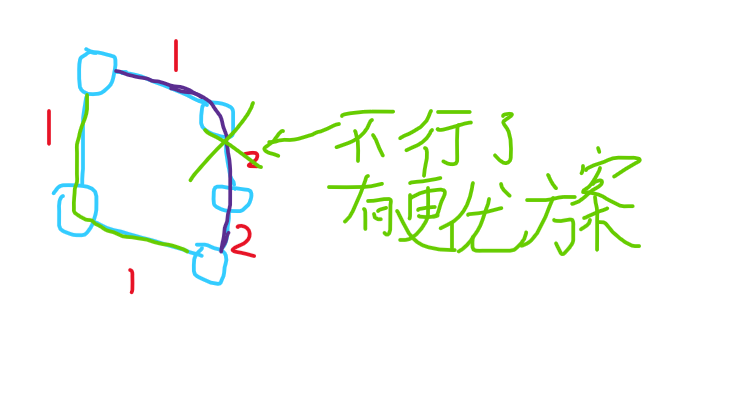
但是该题的初始值不太好弄。有一个解决办法就是因为每次给的数据一定为非负数，所以没有经过的点对应的 \(f\) 值必定为0。遇到这种情况直接更新路径就好。

参考代码：

#include <cstdio>
#include <algorithm>

int f[2020], n, x;

int main(void) {
	scanf("%d", &n);
	
	for(int i=1;i<n;i++) {
		for(int j=i+1;j<=n;j++) {
			scanf("%d", &x);
			if(f[j] == 0) f[j]=f[i]+x;
            //直接更新路径
			else f[j] = std::min(f[j], f[i]+x);
            //否则比较，选择更优的方案
		}
	}
	
	printf("%d\n", f[n]);
	return 0;
}

【做题笔记】P1359租用游艇

原文：https://www.cnblogs.com/BlueInRed/p/12617576.html