这个题实际上是比较难想的,但是题解区的题解都是糊弄了事,有的甚至把紫书上的原话直接搞过来。这里提供一份比较详细的题解。
首先一个很容易想到的做法是用一个 s 数组记录每个结点的当前状态,然后模拟让每一个小球掉落的过程,发现掉落出这棵二叉树的时候就退出。
最后的那个深度除以2(因为这个模拟会使得记录答案的变量多向下跳一个不存在的结点)就是答案。
参考代码:
#include <stdio.h>
#include <string.h>
int s[1<<20];
int main()
{
int n;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
memset(s, 0, sizeof(s));
int D, I;
scanf("%d%d", &D, &I);
int k, sum=(1<<D)-1;
for(int i=1; i<=I; i++)
{
k=1;
for(; ;)
{
s[k]= !s[k];
k= s[k]?(k*2):(k*2+1);
if(k>sum) break;
}
}
printf("%d\n", k/2);
}
}
但是这样做太慢了。其实具体的时间复杂度我也不是很会分析。。。
主要原因是我们记录了太多冗余的信息。在上面的模拟程序中,我们模拟了每一个小球走过的路线,但是实际上我们只需要知道最后一个。
如何比较快的获得最后一个小球(也就是第 \(I\) 个小球)的路径呢?
我们使用队列的思想,假如有一个队列 \(q\) ,一开始把所有的结点入队,然后再按照规则出队,并入队到左、右子树的队列里去。这样,我们就知道了第 \(I\) 个小球在哪个子树中,只要按照同样的方式处理第 \(I\) 个小球所在的子树即可。
但是实际上我们不需要求出这个 \(q\) 队列,也不需要按照上面的方式操作。 上述方式较之直接模拟有了很大的改进,但是注意到第 \(I\) 个小球无论在哪个子树里,始终都是最后入队的。
同时,我们又注意到对于一个结点而言,她只有可能是true或false两种状态。也就是说,这些小球是交替进入左右子树的(true和false一定是交替出现的,因为一个小球就会改变一次状态)。比如说这样:
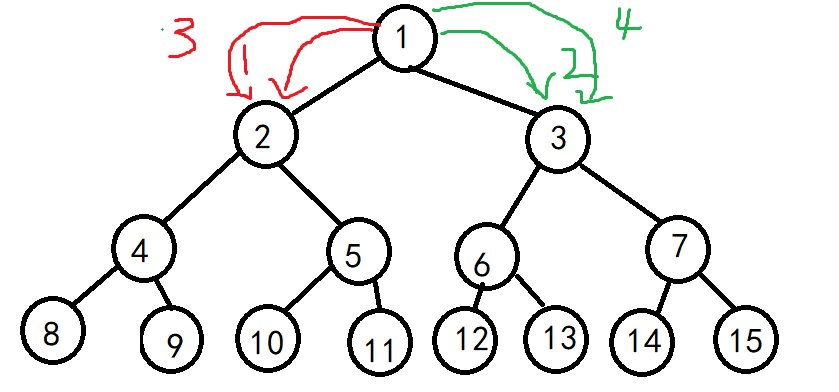
那么也就很自然的注意到,对于任意一个结点而言,若她当前有 \(s\) 个小球,那么在下落时,左、右子树大致各占一半(有可能出现 \(s\) 是负数的情况)。而又由于第 \(I\) 个小球无论在哪个子树里,始终都是最后入队的,所以我们只要知道 \(I\) 的奇偶性,就知道她最终在哪个子树了(这是因为我们每次都先把所有在当前结点的球按照先后顺序放在一起,把这个结点当作根结点操作。)!
Update:如果对上面那句话还是不很理解,可以看一下这里:这个算法每一次把 \(I\) 所在的子树的根作为一个判断的依据。我们把当前结点所在的所有小球重新编号。由于第 \(I\) 个小球在末尾,所以她既是判断哪一个子树的标准也作为当前结点的小球个数。
所以我们只需要知道:
即可。
也就是说,我们只需要模拟 \(D-1\) 次(防止越界),维护 \(I,k\) 即可。
还有一些具体见代码:
#include <stdio.h>
int n;
int main(void)
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
int D, I, k=1;
scanf("%d%d", &D, &I);
for(int j=1; j<D; j++)
if(I%2==1) //奇数,去左子树
{
k= k*2;
//左子树的编号
I= I/2 + 1;
//去左子树的要比去右子树的多一(因为去右子树的都是偶数号的小球)
}
else //偶数,去右子树
{
k=k*2+1;
//右子树的编号
I = I / 2;
//去左、有子树的一样
}
printf("%d\n", k);
//直接输出答案即可
}
return 0;
}
【做题笔记】UVA679 小球下落 Dropping Balls
原文:https://www.cnblogs.com/BlueInRed/p/12617547.html