【LeetCode】不同的二叉搜索树（I、II）

（一）不同的二叉搜索树

题目：96. 不同的二叉搜索树

题目描述：

??给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
   1         3     3      2      1
    \       /     /      / \           3     2     1      1   3      2
    /     /       \                    2     1         2                 3

解题思路：

??本题依旧是对BST性质的一个变形应用，从1到n我们可以首先选择其中某一个值作为根，比如i，那么从1到i-1就可以构建成为左子树，而从i+1到n就可以构建右子树，而总共可以构建的BST的总数是左右子树数量的乘积，这就是典型的子问题，可以用递归来解决。

??除此之外，既然存在递归子问题，我们还可以用动态规划法来解决这一问题。

??我们可以定义两个函数：

• G(n): 长度为n的序列的不同二叉搜索树个数
• F(i,n): 以 i 为根的不同二叉搜索树个数(1<=i<=n)

??不同的二叉搜索树的总数 G(n)，是对遍历所有 i (1 <= i <= n) 的 F(i, n) 之和。换而言之：

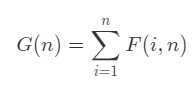
??给定序列 1 ... n，我们选出数字 i 作为根，则对于根 i 的不同二叉搜索树数量 F(i, n)F(i,n)，是左右子树个数的笛卡尔积。

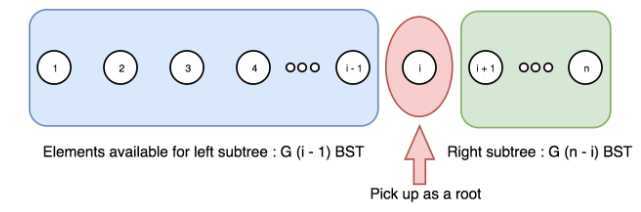
??用公式表示就是：F(i,n)=G(i?1)?G(n?i)

??所以我们可以得到G(n)的递归表达式为：G(0)=1，G(0)=1

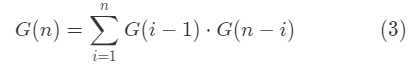
代码实现：

//方法一：递归
class Solution {
    public int numTrees(int n) {
        return numTrees(1,n);
    }
    public int numTrees(int begin,int end){
        if(begin>=end)
            return 1;
        else if(end-begin==1)
            return 2;
        else{
            int res=0;
            for(int i=begin;i<=end;i++){    //以i为根，分别构建左右子树
                int left=numTrees(begin,i-1);
                int right=numTrees(i+1,end);
                res+=(left*right);
            } 
            return res;
        }
    }
}
//方法二：动态规划法
class Solution {
    public int numTrees(int n) {
        int[] dp=new int[n+1];
        dp[0]=1;
        dp[1]=1;

        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i] += dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}

（二）不同的二叉搜索树II

题目：95. 不同的二叉搜索树 II

题目描述：

??给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。

示例：

输入: 3
输出:
[
? [1,null,3,2],
? [3,2,null,1],
? [3,1,null,null,2],
? [2,1,3],
? [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \           3     2     1      1   3      2
    /     /       \                    2     1         2                 3

解题思路：

??本题和上题的题意基本相同，上题只需要求解数量，而本题要返回实际生成的数量，但基本思路也相同， 同样从1到n中以某个值为根，然后分别构建左右子树。具体可以参考代码实现。

代码实现：

class Solution {
    public List<TreeNode> generateTrees(int n) {
        List<TreeNode> res=new ArrayList<>();
        if(n<=0)
            return res;
        return generateTrees(1,n);
    }
    //从begin到end范围可以生成的树的集合
    public List<TreeNode> generateTrees(int begin,int end){
        List<TreeNode> res=new ArrayList<>();
        if(begin>end){
            res.add(null);
            return res;
        }

        for(int i=begin;i<=end;i++){  //以i为根，分别构建左右子树
            List<TreeNode> left=generateTrees(begin,i-1);
            List<TreeNode> right=generateTrees(i+1,end);

            for(TreeNode l:left){   //左右子树分别组装成树
                for(TreeNode r:right){
                    TreeNode root=new TreeNode(i);
                    root.left=l;
                    root.right=r;
                    res.add(root);
                }
            }
        }
        return res;
    }
}

【LeetCode】不同的二叉搜索树（I、II）

原文：https://www.cnblogs.com/gzshan/p/12621221.html