分析算法时,存在几种可能的考虑:
对于最优时间复杂度,其价值不大,因为它没有提供什么有用信息,其反映的只是最乐观最理想的情况,没有参考价值。
对于最坏时间复杂度,提供了一种保证,表明算法在此种程度的基本操作中一定能完成工作。
对于平均时间复杂度,是对算法的一个全面评价,因此它完整全面的反映了这个算法的性质。但另一方面,这种衡量并没有保证,不是每个计算都能在这个基本操作内完成。而且,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算。
因此,我们主要关注算法的最坏情况,亦即最坏时间复杂度。
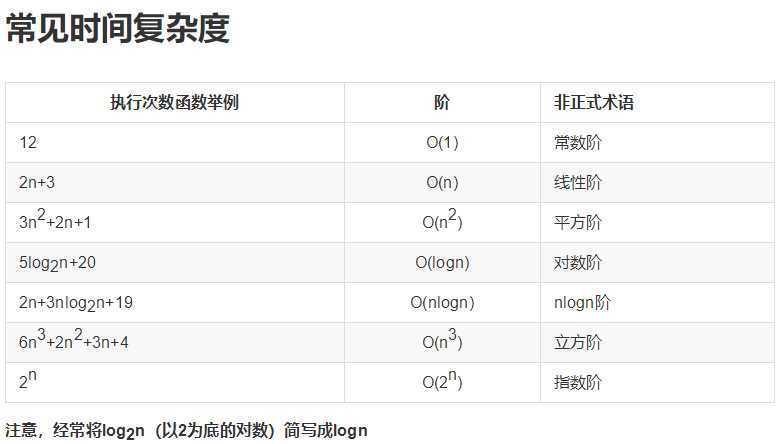
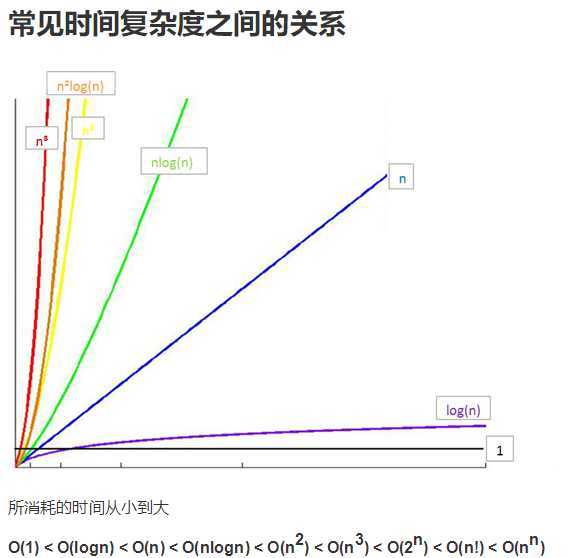

#如果 a+b+c=1000,且 a^2+b^2=c^2(a,b,c 为自然数),如何求出所有a、b、c可能的组合? ‘‘‘ import time start_time = time.time() for a in range(0,501): for b in range(0,501): for c in range(0,501): if a+b+c==500 and a**2+b**2==c**2: print("a,b,c:%d,%d,%d"%(a,b,c)) end_time = time.time() print("time:%d"%(end_time-start_time)) print("finish") ‘‘‘ ‘‘‘ 每台机器执行的总时间不同,但是执行的基本运算数量大体相同 下面我们计算一下以上代码所执行的运算数量 时间复杂度:用运算的步骤数去衡量 T=500*500*500*2 如果用上面的方法计算a+b+c=n n代表咱们解决问题的规模问题 则:T=n*n*n*2 T(n)=n^3*2 T(n)=n^3*k k是与n无关的系数,并不影响整个函数n^3的走势,所以咱们可以忽略 所以可写成 T(n)=k*g(n) g(n)=n^3 这个g函数叫做上面T函数的渐进函数,T(n)=O(g(n))故g函数也叫作一个时间复杂度的大O表示法 ‘‘‘ #上面代码运行时间长62s,改一下,0s import time start_time = time.time() for a in range(0,501): for b in range(0,501): c = 500-a-b if a**2+b**2==c**2: print("a,b,c:%d,%d,%d"%(a,b,c)) end_time = time.time() print("time:%d"%(end_time-start_time)) print("finish") ‘‘‘ 这段代码的时间复杂度为: T(n)=n*n*(1+max(1,0)) =n^2*2 =O(n^2) ‘‘‘
Python内置类型性能分析(列表和字典):
timeit模块:
timeit模块可以用来测试一小段Python代码的执行速度。
Timer是测量小段代码执行速度的类。
stmt参数是要测试的代码语句(statment);
setup参数是运行代码时需要的设置;
timer参数是一个定时器函数,与平台有关。
Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数,默认为1000000次。方法返回执行代码的平均耗时,一个float类型的秒数。

#各种list生成方法 list不能算做基本运算,而是python给我们封装好的东西 ‘‘‘ li1 = [1,2] li2 = [3,4] li = li1+li2 #加操作 实际上是吧li1和li2里的内容拿出来放在一个新列表中,然后让li指向这个新的列表 li = [i for i in range(1000)] #列表生成器 li = list(range(1000)) #可迭代对象直接转换成列表,Pyhon2中无需转换,就是列表 li = [] for i in range(1000): li.append(i) #往空列表中追加 li = [] for i in range(1000): li.extend([i]) ‘‘‘ from timeit import Timer def test1(): li = [] for i in range(1000): li.append(i) def test2(): li = [] for i in range(1000): li+=[i] def test3(): li = list(range(1000)) def test4(): li = [i for i in range(1000)] timer1 = Timer("test1()","from __main__ import test1") #这个测试时跑到另一个地方进行,找到test1()这个函数不能导入“算法引入2list.py”这个名字,而是用__main__代替 print("append:",timer1.timeit(1000)) #打印加操作花费的时间,测1000次 timer1 = Timer("test2()","from __main__ import test2") print("+:",timer1.timeit(1000)) timer1 = Timer("test3()","from __main__ import test3") print("list(range()):",timer1.timeit(1000)) timer1 = Timer("test4()","from __main__ import test4") print("[i for i in range()]:",timer1.timeit(1000)) def test5(): li = [] for i in range(1000): li.insert(0,i) #append是在末尾添加,这个insert参数的0代表总是在开头添加


记住:索引index是O(1),尾部添加append是O(1),在任意位置的弹出pop(i)和插入insert(i,item)是O(n),查找(contains)O(n)
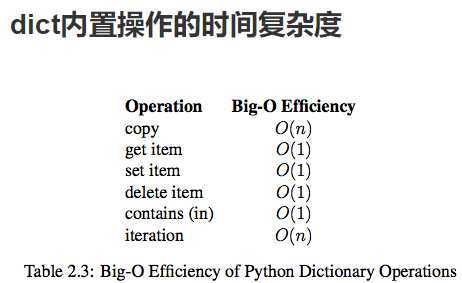
数据结构:
我们如何用Python中的类型来保存一个班的学生信息? 如果想要快速的通过学生姓名获取其信息呢?

列表和字典都可以存储一个班的学生信息,但是想要在列表中获取一名同学的信息时,就要遍历这个列表,其时间复杂度为O(n),而使用字典存储时,可将学生姓名作为字典的键,学生信息作为值,进而查询时不需要遍历便可快速获取到学生信息,其时间复杂度为O(1)
Python给我们提供了很多现成的数据结构类型,这些系统自己定义好的,不需要我们自己去定义的数据结构叫做Python的内置数据结构,比如列表、元组、字典。而有些数据组织方式,Python系统里面没有直接定义,需要我们自己去定义实现这些数据的组织方式,这些数据组织方式称之为Python的扩展数据结构,比如栈,队列等
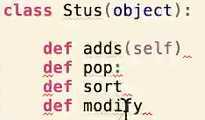
当别人去使用Stus时,只能用我们给他规定好的以上四种方法,具体怎么实现的不用管,抽象数据类型就是把数据类型和数据类型上的运算捆在一起,进行封装
最常用的数据运算有五种:
原文:https://www.cnblogs.com/fenglivoong/p/12618749.html