63 阵列
作者:
问题描述 :
明明在上学的时候,参加数学兴趣班。在班上,老师介绍了一种非常有趣的阵列。
该阵列由n个正整数构成,阵列中的数字从1开始递增,数字的排序规则是从1开始由中间逆时针向外转出,2出现在1的下面,然后直至输出n为止。
例如当n=5的时候,阵列如下:
5
1 4
2 3
当n=9时,阵列如下:
7 6 5
8 1 4
9 2 3
当n=10时,阵列如下:
7 6 5
8 1 4
9 2 3
10
明明回家后想自己动手构造这样的阵列。他从n=1开始构造,但是他发现当n越来越大时,阵列的复杂性就越高,然后构造出来的阵列就越容易出错。为了降低构造阵列的出错率,提高构造速度,明明就求助于你,请你帮他写一个程序,来构造这样的阵列。
明明的问题可以归结为:给你一个正整数n,请你按题目描述中所述的方法,构造出阵列。
输入说明 :
你写的程序要求从标准输入设备中读入测试数据作为你所写程序的输入数据。标准输入设备中有多组测试数据,每组测试数据仅占一行,每行仅有一个正整数n(1≤n≤99),即所要构造的阵列的大小。每组测试数据与其后一组测试数据之间没有任何空行,第一组测试数据前面以及最后一组测试数据后面也都没有任何空行。
输出说明 :
对于每一组测试数据,你写的程序要求计算出一组相应的运算结果,并将这一组运算结果作为你所写程序的输出数据依次写入到标准输出设备中。每组运算结果为一个大小为n的阵列,阵列中的数字用一个空格隔开,具体形式请参考输出样例: 当n为个位数时,输出的每个数占1位,当n为两位数时,两位数所在的列输出的每个数占2位(不足2位的左边补空格)。 每组运算结果与其后一组运算结果之间有一个空行,最后一组运算结果之后没有任何空行。 注:通常,显示屏为标准输出设备。
输入范例 :
5
45
10
输出范例 :
5
1 4
2 3
43 42 41 40 39 38 37
44 21 20 19 18 17 36
45 22 7 6 5 16 35
23 8 1 4 15 34
24 9 2 3 14 33
25 10 11 12 13 32
26 27 28 29 30 31
7 6 5
8 1 4
9 2 3
10
解题思路:(最近状态很差,总想玩游戏。)我觉得这道题目由一下几个问题值得探究
1、首元素1的坐标(i,j)如何确立?
观察,总结模糊规律(其实只要矩阵数组开的足够大即可)。我采取的是模糊规律。
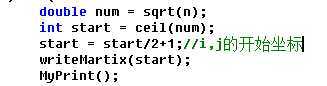
ceil();函数是向上取整,为了防止意外产生,在实际确定首元素初始坐标时,我加了保险(+1)。
2、如何模拟给矩阵赋值的过程,首先计数器循环加到n为止,然后观察数学规律。每次走的路径大致为

但是这个路径是不准确的,我们可以对它进行修正。我们发现每次给矩阵某元素赋值操作之后,它总有转弯的倾向
(逆时针直角弯),但是不一定成功。则按上一次方向直行,下次继续倾向转弯。如果可以转弯则优先转弯,否则走上一次
老路。

3、注意矩阵大小,边界(墙),还要记录实际赋值的围墙边界(输出的时候用)。
4、关于格式的注意事项。这道题目格式搞了我很长时间。
题目要求如下:

在实际操作中,我犯了很多错误,最典型的
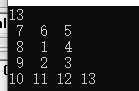
看似没有任何问题,但是加入可见字符后(将输出的空格换成可见字符,检查格式)如下
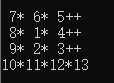
前三行最后面多输出了空格,应当去掉!
好了,完整代码
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <math.h> 4 #include <string.h> 5 #include <ctype.h> 6 7 8 #define maxn 15 9 10 int martix[maxn][maxn]; 11 12 int hash[maxn]; 13 14 int X[] = {1,0,-1,0}; 15 int Y[] = {0,1,0,-1}; 16 int m = 0; 17 int n; 18 int mini,minj,maxi,maxj; 19 void writeMartix(int start); 20 void InitMartix(); 21 void MyPrint(); 22 int main(){ 23 24 InitMartix();//初始化矩阵一次即可 25 int flag = 0; 26 while(scanf("%d",&n)!=EOF){ 27 InitMartix(); 28 29 if(flag == 1){ 30 printf("\n"); 31 } 32 flag = 1; 33 mini = minj = 100; 34 maxi = maxj = -1; 35 36 if(n == 1){ 37 printf("%d\n",1); 38 }else if(n==2){ 39 printf("%d\n%d\n",1,2); 40 }else{ 41 double num = sqrt(n); 42 int start = ceil(num); 43 start = start/2+1;//i,j的开始坐标 44 writeMartix(start); 45 MyPrint(); 46 } 47 48 } 49 50 return 0; 51 } 52 53 54 void writeMartix(int start){ 55 int i,j,idx; 56 int num = 1; 57 //printf("%d ===\n",start); 58 i = j = start; 59 idx = 3; 60 int x,y; 61 62 while(num<=n){ 63 martix[i][j] = num; 64 if(i<mini){ 65 mini = i; 66 } 67 if(j<minj){ 68 minj = j; 69 } 70 71 if(i>maxi){ 72 maxi = i; 73 } 74 if(j>maxj){ 75 maxj = j; 76 } 77 num++; 78 idx = (idx+1)%4; //提前预定转弯 79 x = i + X[idx]; 80 y = j + Y[idx]; 81 82 if(martix[x][y] == -1){ 83 //OK 84 i = x; 85 j = y; 86 }else{ 87 //转弯失败,回退 88 idx = (idx-1+4)%4; 89 x = i + X[idx]; 90 y = j + Y[idx]; 91 i = x; 92 j = y; 93 } 94 95 //printf("%d 96 } 97 } 98 99 void InitMartix(){ 100 int i,j; 101 102 for(i=0;i<15;i++){ 103 for(j=0;j<15;j++){ 104 martix[i][j] = -1; 105 } 106 } 107 } 108 109 void MyPrint(){ 110 int i,j; 111 int count = 0; 112 113 for(j=minj;j<=maxj;j++){ 114 hash[j] = 1;//默认输出一位 115 for(i=mini;i<=maxi;i++){ 116 if(martix[i][j]>=10){ 117 hash[j] = 2; 118 break; 119 } 120 } 121 } 122 for(i=mini;i<=maxi;i++){ 123 for(j=minj;j<=maxj;j++){ 124 if(martix[i][j]==-1){ 125 if(j==maxj){//去掉每行后面的空格 126 break; 127 } 128 if(hash[j]==1){ 129 printf(" "); 130 }else{ 131 printf(" "); 132 } 133 if(j!=maxj){ 134 printf(" "); 135 } 136 // 137 }else{ 138 if(hash[j]==1){ 139 printf("%d",martix[i][j]); 140 }else{ 141 printf("%2d",martix[i][j]); 142 } 143 count++; 144 if(count == n){ 145 break; 146 } 147 martix[i][j] = -1;//复原矩阵 148 if(j!=maxj&&count!=n&&martix[i][j+1]!=-1){ 149 printf(" "); 150 } 151 } 152 153 } 154 printf("\n"); 155 156 } 157 }
原文:https://www.cnblogs.com/ManOK/p/12621320.html