词典:[我们, 去, 爬山, 今天, 你们, 昨天, 跑步]
One-Hot representation
每个单词的表示:
我们: [1, 0, 0, 0, 0, 0, 0]
爬?: [0, 0, 1, 0, 0, 0, 0]
运动: [0, 0, 0, 0, 0, 0, 1]
昨天: [0, 0, 0, 0, 0, 1, 0]
向量大小和词典的大小是相同的
假设我们的词典里有7个单词: [我们,又, 去,爬山,今天,你们,昨天,跑步]
每个句子的表示:
我们 今天 去 爬山 :[1, 0, 1, 1, 1, 0, 0, 0]
你们 昨天 跑步 :[0, 0, 0, 0, 0, 1, 1, 1]
你们 又 去 爬山 又 去 跑步 :[0, 1, 1, 1, 0, 1, 0 ,1]
向量和词典大小相同,向量的元素和词典的词是对应的,第一个元素是指词典中第一个单词有没有出现,第二个元素是指词典第二个词有没有出现...
和boolean不同的是,关注出现次数
假设我们的词典里有7个单词: [我们,又, 去,爬山,今天,你们,昨天,跑步]
每个句子的表示:
我们 今天 去 爬山 :[1, 0, 1, 1, 1, 0, 0, 0]
你们 昨天 跑步 :[0, 0, 0, 0, 0, 1, 1, 1]
你们 又 去 爬山 又 去 跑步 :[0, 2, 2, 1, 0, 1, 0 ,1]
又 和 去 都出现了两次,因此都是2
计算距离
欧式距离
d=|s1-s2|
S1: 我们 今天 去 爬山 =[1, 0, 1, 1, 1, 0, 0, 0]
S2: 你们 昨天 跑步 =[0, 0, 0, 0, 0, 1, 1, 1]
S3: 你们 又 去 爬山 又 去 跑步 =[0, 2, 2, 1, 0, 1, 0 ,1]
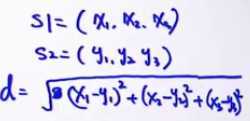
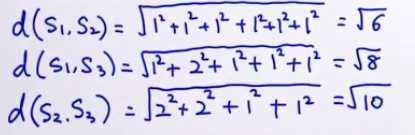
所以sim(S1, S2) > sim(S2, S3),sim(S1, S3) > sim(S2, S3)
余弦相似度
方向和大小都考虑

s1*s2 内积
|s1| |s2| 范数

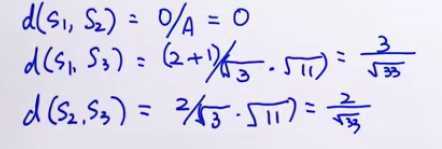
count表示的缺陷:并不是出现的越多越重要,并不是出现的越少越不重要
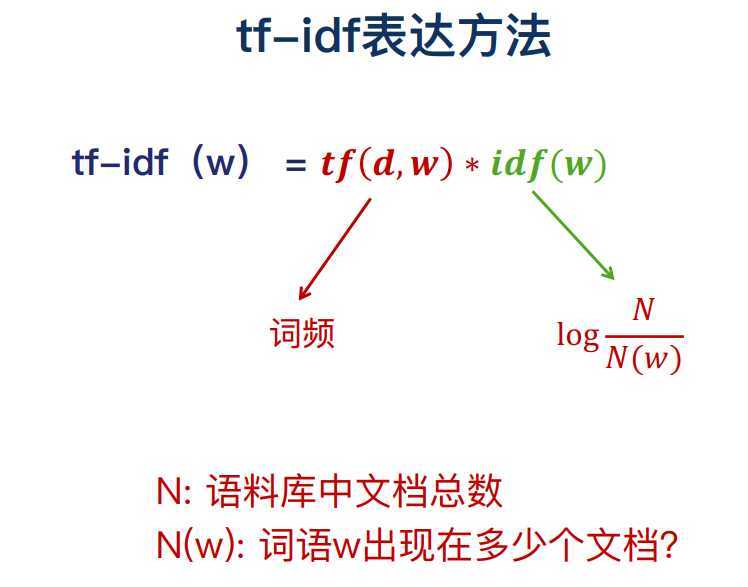
如果只考虑词频的项,和count是一样的
idf(w)考虑单词的重要性,如果很多文档都有一个词,这个词反而不重要。

定义词典:[今天 上 NLP 课程 的 有 意思 数据 也]
词典大小为9
下面计算 tf-idf 向量
句子1

句子2
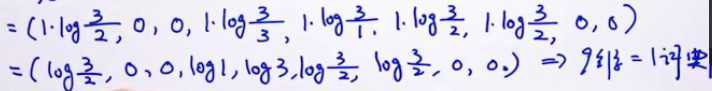
句子3
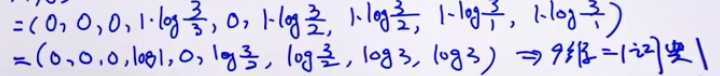
衡量句子的相似性 one-hot representation:
下面哪些单词之间语义相似度更更高?
我们,爬山,运动,昨天
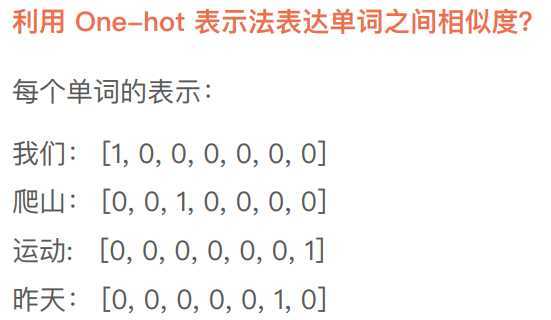
计算欧式距离都是相等的,不能判断单词间的相似度

余弦相似度也是相等的

one-hot representation无法表达单词的语义相关度
稀疏性

词典可能会非常大,比如新华词典,转为向量后,是个维度非常高的系数矩阵
因此,one-hot representation有两个缺点:
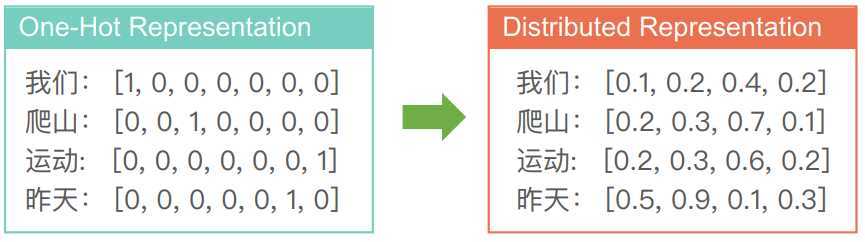
用分布式衡量单词相似度
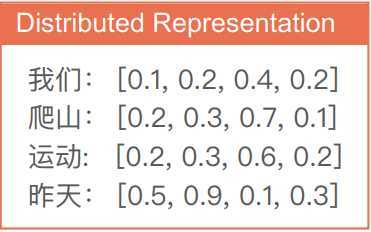
欧式距离

针对单词的分布式表示方法就是词向量(word vectors)
输入:字符串
1B或10B的量级,即字符串要包含10的9次方或10次方的单词
模型:深度学习模型
Skip-Gram Glone CBOW RNN/LSTM MF
参数 dim/D 多少维的词向量
输出:词向量
理想情况词向量代表单词的意思,词向量在某种程度上可以认为代表了单词的意思
检验词向量是否能捕获单词的意思
有了单词的分布式表示,如何表示句子呢?最常用的是评价法则。


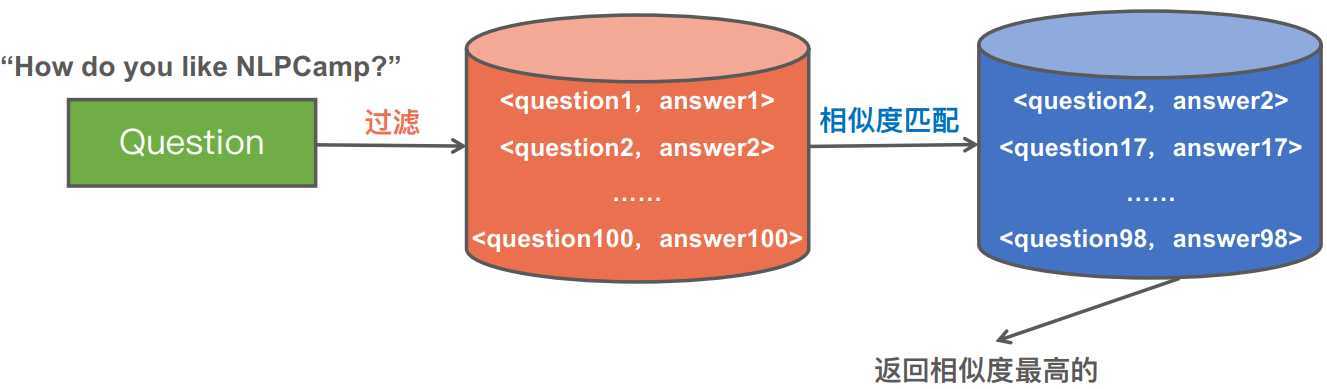
知识库中如果有N个Question和Answr对,就要计算N次相似度
复杂度是O(N)
如何降低时间复杂度
核心思路:层次过滤思想
层层过滤,最后只剩少部分问题答案对,进行相似度计算
各层的复杂度是递增的
如下图100个答案,过滤后剩下很少
假设搜索引擎爬取了四个文档
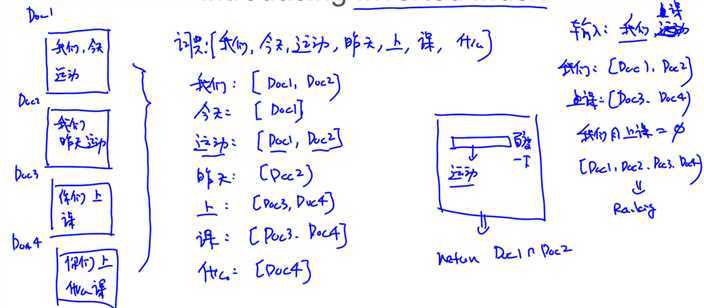
假如搜索运动,去四个文档里一一搜索复杂度会很高,如果有倒排表,只需返回去对应的文档
搜索 我们 上课,去倒排表查看出现在哪些文档里,这些文档是doc1、doc2、doc3和doc4,且我们 上课并没有同事出现在一个文档中,于是将这四个文档都返回
接着上面问答系统
我们可以将所有的问题中的单词建立倒排表
第一层过滤可以是,找到包含问题每个单词的知识库中的问题
如,找到所有包含how的问题,所欲包含 do 的问题,包含 you 的问题,包含 like 的问题,包含 NLPCamp 的问题
如果还是很多,可以加第二层过滤
如,找到同时包含两个单词的知识库中的问题
只需要计算过滤后剩下的问题的相似度即可
原文:https://www.cnblogs.com/aidata/p/12622034.html