1 模型评价指标

模型评估包括评估方法（evaluation）和评价指标（metrics）。评估方法包括留出法，交叉验证，包外估计等。本文只介绍评价指标。

评价指标的两个作用：一是了解模型的泛化能力，可以通过同一个指标来对比不同模型，从而知道哪个模型相对好，那个模型相对差；二是可以通过这个指标来逐步优化我们的模型。

对于分类和回归两类监督学习，分别有各自的评判标准。本篇主要讨论与分类相关的一些指标，包括混淆矩阵、准确率、（宏/微）查准率、查全率、F1指数、PR曲线、ROC曲线/AUC。其中4个单一指标比较简单，重点说下混淆矩阵、PR曲线和ROC曲线。

2 混淆矩阵、准确率、查准率、查全率

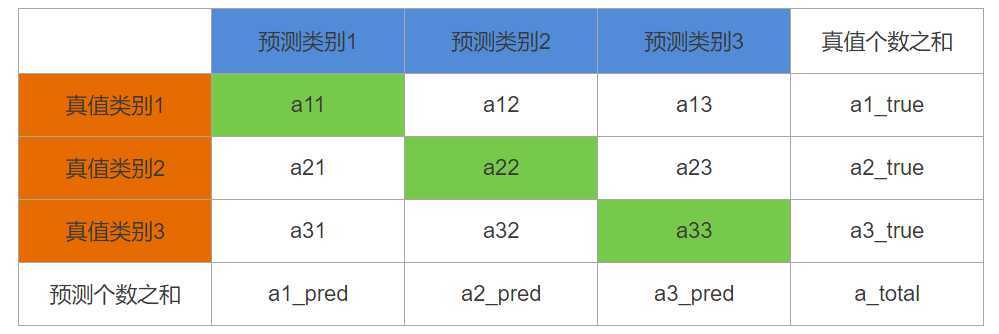
混淆矩阵：假设有三个类别需要分类，现在训练了一个分类模型，对验证集的预测结果列成表格，每一行是真正的类别，每一列是预测的类别，这个列表矩阵即为混淆矩阵。如下所示，混淆矩阵中土黄色表示真实类别，蓝色表示预测类别，那么对角线上绿色值就表示预测正确的个数，某个绿色值除以当前行之和就是该类别的查全率（recall），除以当前列之和就是该类别的查准率（precision），对角线之和除以总和就是全局准确率（accuracy）。比如现在的分类器，它的accuracy为(a11+a22+a33)/a_total，它对类别1的查全率为a11/a1_true，查准率为a11/a1_pred。混淆矩阵的优势在于囊括了下面几种单一指标，各种类别的信息一目了然。

准确率（accuracy）：最原始的评价指标，将正负样本统一看待，只要预测正确就算数，\(\frac{TP+TN}{P+N}\)。虽然准确率可以判断总的正确率，但是在样本不平衡的情况下，导致了得到的高准确率结果含有很大的水分。因此衍生出了其它两种指标：查准率和查全率。

查准率（precision）：预测为正的样本里面，真的正样本所占比例，\(\frac{TP}{TP+FP}\)。

查全率（recall，也称召回率）：所有正样本里面检测出来的比例，\(\frac{TP}{TP+FN}\)。

3 PR曲线和F1值

查准率和查全率都依赖于阈值的选取。以逻辑回归为例，预测概率值大于某个阈值则判定为正样本，小于该阈值则判定为负样本。但问题是：这个阈值是我们随便定义的，我们并不知道这个阈值是否符合我们的要求。因此，为了更进一步了解模型的性能，我们希望遍历 0 到 1 之间所有的阈值，看看在各个阈值下的查准率和查全率。

PR曲线的绘制：首先拿到分类器对于每个样本预测为正例的概率，根据概率对所有样本进行逆序排列，然后将分类阈值设为最大，即把所有样本均预测为反例，然后依次放出一个样本作为正例，分别画出precision和recall。以precision作为纵轴，recall作为横轴，将所有点连起来即得到PR曲线。

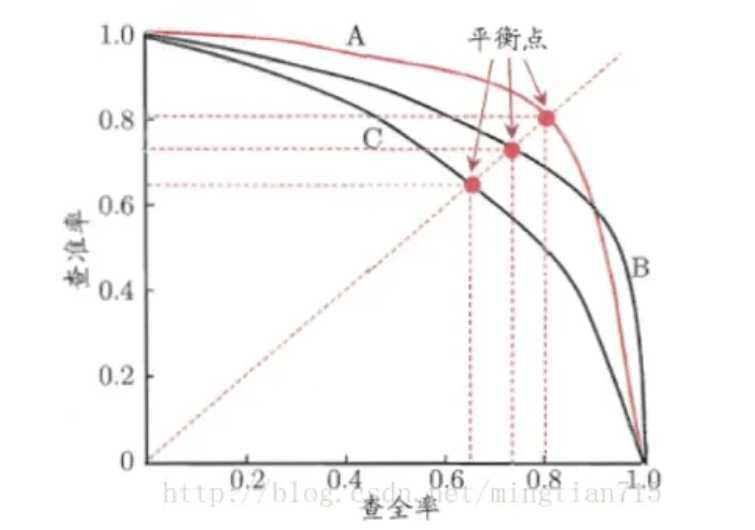
PR曲线的含义：

• PR曲线的意义在于，可以直观看出precision随着recall增大的变化率。如果曲线越接近右上角，就说明随着recall的增加，precision往下掉的速度不明显。这是个好事情，说明如果需要的话，可以调整阈值以增加recall，而不用担心precision掉的太厉害。
• 如果正样本的比例为α，那么随便猜的情况下，PR曲线下的面积就是α。所以与ROC的AUC不同，即使PR曲线下面积小于0.5，也不能说明它差，因为要考虑正负样本比例。可以参考这里
• PR曲线下面积就等于平均精度(average precision)。目标检测中经常用PR曲线下面积来计算AP（经过插值），以评估目标检测模型的性能。

查准率和查全率是一对矛盾体，一个指标增加时，另一个往往就减少。当比较两个模型的优劣时，PR曲线往往会相交，因此为了直观看出哪个模型更好，就需要一个综合考虑两者的数值，这个值就是F1值。

F1指数：查准率和查全率的几何平均值的2倍，即\(\frac{2}{\frac{1}{P}+\frac{1}{R}}\)。如果希望F1值高，则需要两者都比较高且均衡。

4 ROC曲线

ROC曲线的横轴是假正例率\(\frac{FP}{所有负样本}\)，纵轴是真正例率\(\frac{TP}{所有正样本}\)（即召回率）。

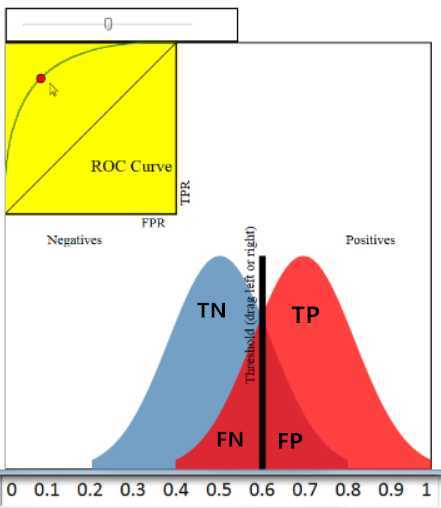
ROC曲线的绘制：和PR曲线的绘制过程类似，只不过是每次放出一个样本作为正例时，分别画出真正例率和假正例率。以真正例率作为纵轴，假正例率作为横轴，将所有点连起来即得到ROC曲线。曲线越靠近左上角，意味着越多的正例优先于负例，模型的整体表现也就越好。

那么问题来了：为啥有了混淆矩阵和PR曲线，还要ROC？这里解释ROC的两大厉害之处。

厉害之处1：AUC(Area Under Curve)。这里的AUC是指ROC曲线下面积，根据这个值，可以大致判断模型的分类能力。我们知道，对于一个好的逻辑回归模型，它能把负样本的预测值压得很低（尽可能接近0），把正样本的预测值拉的很高（接近1），这样一来，我们只需要找到一个比较合适的阈值，就能很好的把正负样本分开。那对于现在已经训练好的逻辑回归模型，该如何知道它把样本分开的能力呢？就可以用ROC的AUC。

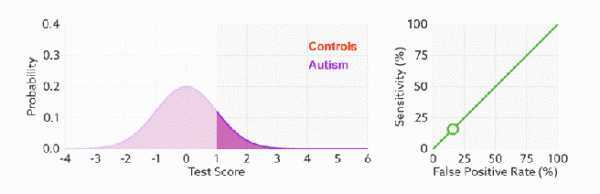
图中的两个正态分布表示两个类别的概率密度，模型越好，就能把两个类别分的越开。可以看出，模型把两个类别分的越开，对应的ROC曲线就越接近左上角，AUC就越大。最理想的情况是AUC等于1，最差的情况是AUC等于0.5（两个类别概率密度重合在一块了，即模型没能把两个类别分开）。所以一般 AUC 的值是介于 0.5 到 1 之间的。AUC 的一般判断标准：

• 0.5 - 0.7：效果较低，但用于预测股票已经很不错了
• 0.7 - 0.85：效果一般
• 0.85 - 0.95：效果很好
• 0.95 - 1：效果非常好，但一般不太可能

注：资料中说，曲线下面积可以看作是模型将某个随机正类别样本排列在某个随机负类别样本之上的概率。其实表达的就是，曲线下面积可以代表模型将正负样本分开的能力。

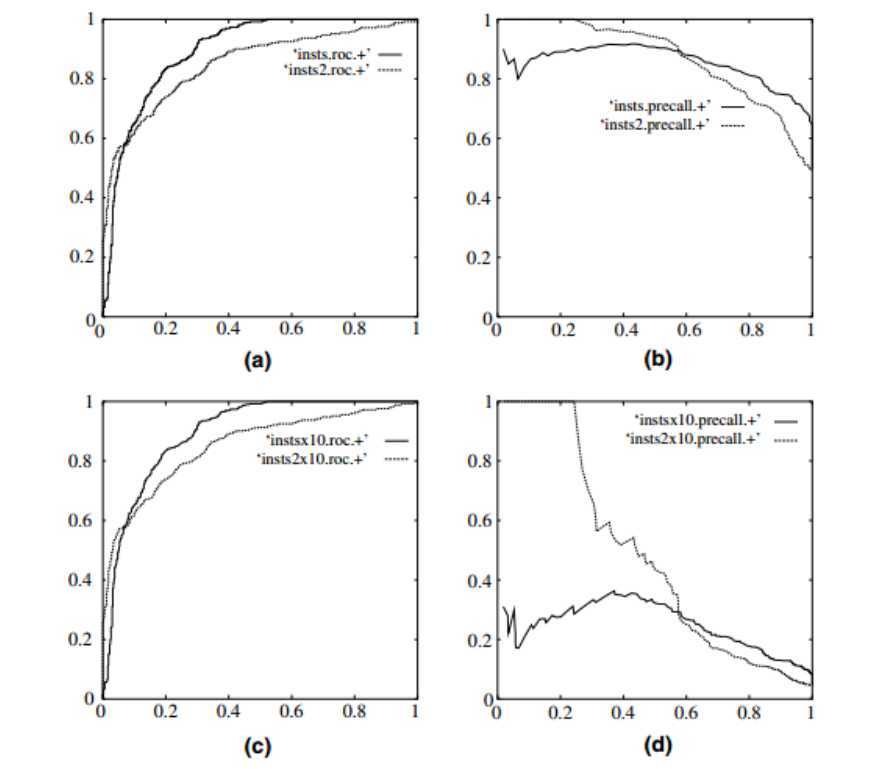
厉害之处2：对样本类别不平衡的问题不敏感。ROC曲线兼顾正例和负例的权衡。因为TPR聚焦于正例，FPR聚焦于与负例，使其成为一个比较均衡的评估方法。两个指标都不依赖于具体的类别分布。而PR曲线的两个指标查准率和查全率都聚焦于正例。当负样本数量突然增大时，ROC基本不变，但PR曲线变化很大。比如下图，参考文献中举了个例子，负例增加了10倍，ROC曲线没有改变，而PR曲线则变了很多。

5 应用场景

precision和recall的应用场景：

• 查准率在意的是，预测为正的样本中有多少是真的正样本；而查全率在意的是，所有真的正样本中到底有多少被检测出来。比如在审判犯罪嫌疑人时，我们希望司法系统的查准率越高越好，即尽量不要冤枉无辜者，因为误判为正样本的后果很严重；
• 而对于银行的欺诈检测系统来说，通常希望它的查全率越高越好，即尽量把欺诈账户识别出来，因为漏检可能会带来很大损失，而误判为正样本的话则影响不大。

PR曲线和ROC曲线应用场景：

• ROC曲线兼顾正例与负例，而PR曲线完全聚焦于正例，所以前者适用于评估分类器的整体性能，以及需要剔除类别不平衡影响的情况，而PR曲线适用于评估更看重正例的情况。
• 如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合。
• 在信息检索、推荐中，希望precision较大，用户希望排名靠前的推荐是自己想要的结果，所以评估时PR曲线比较合适。

6 小结

• 混淆矩阵可以得到多种单一指标，各种类别的信息一目了然
• precision和recall是一对矛盾体，前者体现的是预测的正例靠不靠谱，后者体现的是漏检率
• PR曲线、ROC曲线可以呈现出不同的阈值下的信息，而单一指数只能看出单一阈值下的信息
• PR曲线可以直观看出precision随着recall增大时下降速度；即使PR曲线下面积小于0.5，也不能说明它差，需要考虑正负样本比例
• ROC曲线两大厉害之处在于，一：AUC能反映出分类器对样本的排序能力，AUC越大，能将正负样本分的越开。二：ROC曲线对样本类别不平衡的问题不敏感。

Reference：

• https://www.6aiq.com/article/1549986548173
• http://wenda.chinahadoop.cn/question/3188
• https://www.dataschool.io/roc-curves-and-auc-explained/
• https://www.cnblogs.com/massquantity/p/8592091.html

几种常见的模型评价指标

原文：https://www.cnblogs.com/inchbyinch/p/12622667.html