* ! TJOI2018party

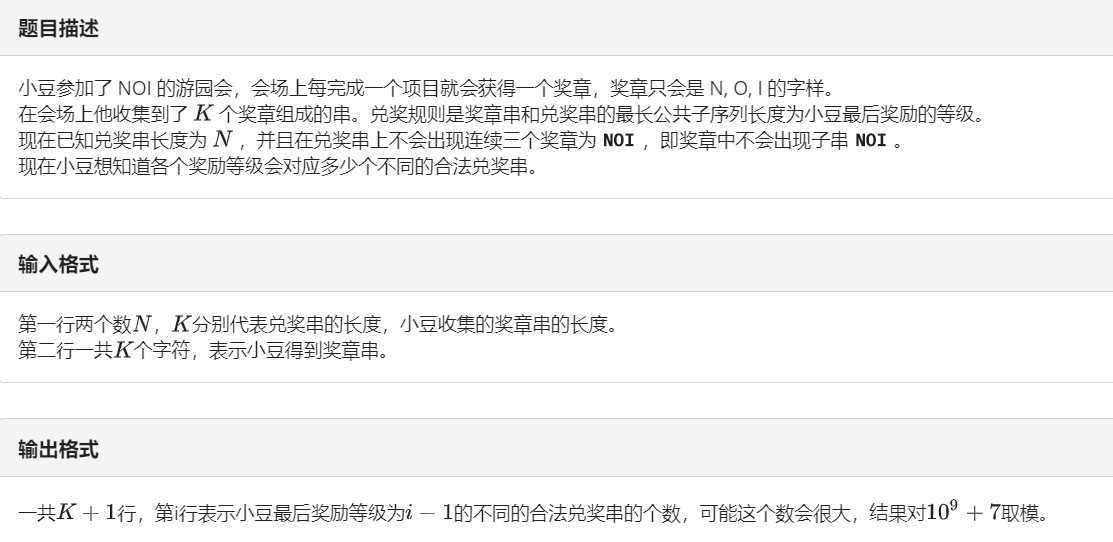
\(f[i][j][u]\)i位，j个相同，与NOIu个相同的方案数

打出来发现不对，公共子序列又不是公共前缀

菜死了，又去看题解了┭┮﹏┭┮

SOL：

又是一道非常妙的思维题！

两个序列的最长公共子序列\(f_{i,j}\)

k又非常小，于是考虑吧上述DP写入状态

\(dp_{i,j,u}\)长度为i的字符串与k的每一个前缀的DP状态压缩下来为j，与NOI匹配了u为的方案数

可以发现j这个DP状态的值一定是单调递增且相邻两位相差不超过1，可以以差分的形式二进制存下（即前缀和才是真实的值）

时间复杂度\(O(n2^kk)\)

对于字符串题的话我们满足别的限制基本就是建一个自动机来搞定别的限制条件……像什么Ac自动机后缀自动机之类的都可以帮我们搞定一些但不是全部的限制条件——摘自洛谷题解

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;char c=getchar();
	while(!isdigit(c)){if(c==‘-‘)f=-1;c=getchar();}
	while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f==1?x:-x;
}
const int mod=1e9+7;
int n,k,cur,a[20],ans[20],f[2][40000][4];
char ch[20];
inline int getnxt(int s,int p){
	int ret=0;
	for(int i=1,nw_1=0,las=0,las_1=0,nw;i<=k;i++){
		if((s>>i-1)&1)las++;
		nw=max(nw_1,las);
		if(p==a[i])nw=max(nw,las_1+1);
		if(nw>nw_1)ret|=(1<<i-1);
		nw_1=nw;las_1=las;
	}
	return ret;
}
int main(){
	n=read();k=read();
	scanf("%s",ch+1);
	for(int i=1;i<=k;i++)	
		if(ch[i]==‘O‘)a[i]=1;
		else if(ch[i]==‘I‘)a[i]=2;
	f[0][0][0]=1;
	for(int i=1,uu,ss;i<=n;i++){
		cur^=1;
		memset(f[cur],0,sizeof(f[cur]));
		for(int s=0;s<(1<<k);s++)
			for(int u=0;u<3;u++){
				if(!f[cur^1][s][u])continue;
				for(int p=0;p<3;p++){
					uu=(p==u)?u+1:(!p);
					if(uu==3)continue;
					ss=getnxt(s,p);
					(f[cur][ss][uu]+=f[cur^1][s][u])%=mod;
				}
			}
	}
	for(int s=0,bit;s<(1<<k);s++){
		bit=0;
		for(int i=1;i<=k;i++)
			if((s>>i-1)&1)bit++;
		for(int u=0;u<3;u++)
			(ans[bit]+=f[cur][s][u])%=mod; 
	}
	for(int i=0;i<=k;i++)cout<<ans[i]<<"\n";
	return (0-0);
}

* ! TJOI2018party

原文：https://www.cnblogs.com/aurora2004/p/12622727.html