Aizu ALDS1_6_D Minimum Cost Sort
直接排序太简单了，我们来考虑一下排序的代价，对于一个长度n的由非负整数组成的数组，我们用交换法排序，每次可以交换任意两个元素，而交换的代价，是这两个元素之和，求出排序的最少交换代价，保证数组里没有两个元素相同且元素值小于等于10000
第一行输入n，第二行输入n个非负整数，1<n<=1000
输出排序的最小代价
5 1 5 3 4 2
7
思路：
使用成环交换排序取最小代价
方法：
我们以W = {4, 3, 2, 7, 1, 6, 5}为例进行分析。现在的目标是求出将W重排为{1, 2, 3, 4, 5, 6, 7}时所需的最小成本。我们不妨先画出一张标出每个元素最终将移动到哪个位置的草图。（如图1所示）
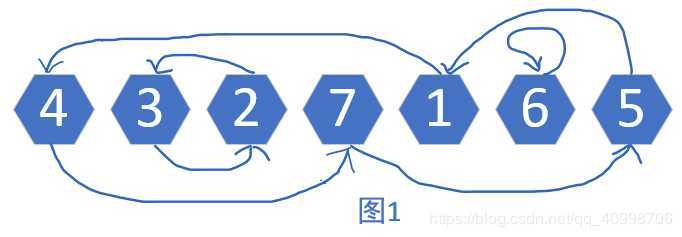
图中有3个闭合的圆，分别是4 - 7 - 5 - 1 - 4；3 - 2 - 3；6 - 6。现在我们来分析每个圆所需的最小成本。
为自环即1长度的圆无需移动，成本为0。
长度为2交换位置即可，成本为二者之和。如3 - 2 - 3的成本为3 + 2 = 5。
对于长度大于等于3的圆。（如图2所示）在处理4 - 7 - 5 - 1 - 4时，通过1来移动其他元素可以保证成本最小。
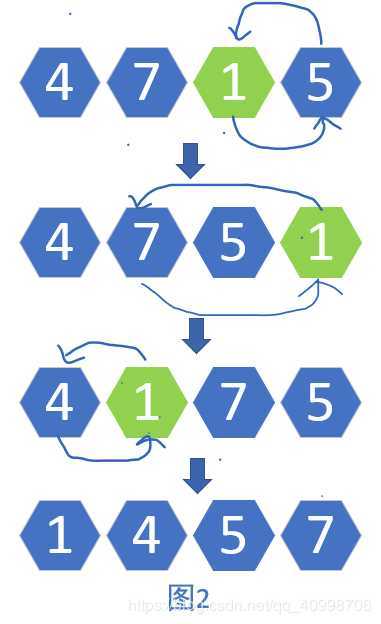圆中的元素为wi，圆内元素数为n，那么此时的成本为Σwi+(n−2)∗min(wi)\Sigma wi+ (n-2)*min(wi)Σwi+(n−2)∗min(wi)
由于各元素至少移动一次，所以有Σwi\Sigma wiΣwi。再加上最小值在最后一次交换前要移动(n - 2)次，所以有(n - 2) * min(wi)。上式在n = 2时也成立。
于是最小成本为(5 + 0) + (17 + 2) = 24。
这个方法乍眼一看像那么回事，但是你仔细一寻思发现还存在反例。（如图3所示）
如果套用之前的方法，1 - 2 - 1成本为3，8 - 10 - 9 - 7 - 8成本为48，总成本为51。
但若先将7和1交换，把圆8 - 10 - 9 - 7 - 8改为8 - 10 - 9 - 1 - 8，这部分的成本就成了28 + 2 * 1 = 30。然后再加上两次交换7和1以及圆1 - 2 - 1的成本，总成本为49。可见，即便我们多加了两次1和7交换的成本，总成本依然小于之前的方法，显然有时从圆外借元素来移动，能让成本更低。
设外圆的元素为x。借元素增加的成本为2∗(min(wi)+x)2*(min(wi)+x)2∗(min(wi)+x)，节约的成本为(n−1)∗(min(wi)−x)(n-1)*(min(wi)-x)(n−1)∗(min(wi)−x)此时该部分的总成本为
Σwi+(n−2)∗min(wi)+2∗(min(wi)+x)−(n−1)∗(min(wi)−x)=Σwi+min(wi)+(n+1)∗x\Sigma wi+(n-2)*min(wi)+2*(min(wi)+x)-(n-1)*(min(wi)-x)=\Sigma wi+min(wi)+(n+1)*xΣwi+(n−2)∗min(wi)+2∗(min(wi)+x)−(n−1)∗(min(wi)−x)=Σwi+min(wi)+(n+1)∗x
可见x应选用整个输入中最小的元素。
综上，程序需要计算“借整体最小元素”与“不借元素”的两种情况，选出其中成本较小的一方。
#include<bits/stdc++.h> #define INF 0x3f3f3f3f #define DOF 0x7f7f7f7f #define mem(a,b) memset(a,b,sizeof(a)) #define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); typedef long long ll; using namespace std; const int maxn=1e5+10; int n; int a[maxn],b[maxn],vis[maxn]; ll solve() { map<int,int>mt; int x=INF; for(int i=1;i<=n;++i) { b[i]=a[i]; x=min(x,a[i]); } sort(b+1,b+1+n); for(int i=1;i<=n;++i) mt[b[i]]=i; ll ans=0; for(int i=1;i<=n;++i) { ll cnt=0,sum=0,minn=INF,tmp=i; while(1) { vis[tmp]=1; ++cnt; minn=min(minn,a[tmp]*1ll); sum+=a[tmp]; tmp=mt[a[tmp]]; if(vis[tmp]) break; } ans=ans+min(sum+(cnt-2)*minn,sum+(cnt-2)*minn+2*(minn+x)-(cnt-1)*(minn-x)); } return ans; } int main() { cin>>n; for(int i=1;i<=n;++i) cin>>a[i]; ll ans=solve(); cout<<ans<<endl; }
const int maxn=1e5+10; int n; int a[maxn],b[maxn],vis[maxn]; ll solve() { map<int,int>mt; int x=INF; for(int i=1;i<=n;++i) { b[i]=a[i]; x=min(x,a[i]); } sort(b+1,b+1+n); for(int i=1;i<=n;++i) mt[b[i]]=i; ll ans=0; for(int i=1;i<=n;++i) { ll cnt=0,sum=0,minn=INF,tmp=i; while(1) { vis[tmp]=1; ++cnt; minn=min(minn,a[tmp]*1ll); sum+=a[tmp]; tmp=mt[a[tmp]]; if(vis[tmp]) break; } ans=ans+min(sum+(cnt-2)*minn,sum+(cnt-2)*minn+2*(minn+x)-(cnt-1)*(minn-x)); } return ans; }
const int maxn=1e5+10; int n; int a[maxn],b[maxn],vis[maxn]; ll solve() { map<int,int>mt;//用来存环的序号 int x=INF; for(int i=1;i<=n;++i) { b[i]=a[i]; x=min(x,a[i]);//全局最小值 } sort(b+1,b+1+n); for(int i=1;i<=n;++i) mt[b[i]]=i;//取每个元素的序号 ll ans=0; for(int i=1;i<=n;++i) { ll cnt=0,sum=0,minn=INF,tmp=i; while(1)//成环判断 { vis[tmp]=1; ++cnt; minn=min(minn,a[tmp]*1ll); sum+=a[tmp]; tmp=mt[a[tmp]]; if(vis[tmp]) break; } ans=ans+min(sum+(cnt-2)*minn,sum+(cnt-2)*minn+2*(minn+x)-(cnt-1)*(minn-x));//取两种的最小代价 } return ans; }
原文：https://www.cnblogs.com/waryan/p/12628202.html