可持久化线段树学习笔记

最近学习了毒瘤的可持久化线段树，为了避免自己忘记，我决定还是做个笔记比较好，如果有什么问题欢迎大佬指出

可持久化是真的毒瘤，在网上找了很多资料才搞懂
(不过我觉得应该是我太蒻了)

首先以洛谷上的两个板子题为例吧:

• P3834 【模板】可持久化线段树 1（主席树）

• P3919 【模板】可持久化数组（可持久化线段树/平衡树）

对于第一题，要求询问区间第K大(第K大指的是从小到大排序的第K个)，直接扫是肯定不行的，因此我们需要可持久化线段树(感觉跳的好快，但是我也不清楚要怎么表达，就这样吧，反正知道是要用这个就行了)

首先既然是可持久化线段树，那么肯定需要用到线段树的，但是对于一般的线段树，每个节点维护的是对应区间的最值或者是和积，用这种线段树写可持久化我觉得是肯定不行的(emmm具体怎么样我也不清楚)

因此我们维护的是属于对应区间的元素的个数，建树代码如下，要注意开始需要排序后离散化:

struct Tree{
    int left;
    int right;
    int size;
}node[5000001];  //用结构体存树节点的左孩子，右孩子和当前的权值 
int tot_,a[5000001],b[5000001],N;
int Build_ (int L,int R){
	int now=++tot_; //now为当前节点编号 
    int mid=(L+R)>>1; //获取区间中点 
    if (L!=R){ //边界 
    node[now].left=Build_ (L,mid); //向左建树 
    node[now].right=Build_ (mid+1,R); //向右建树 
    }
    return now;
}
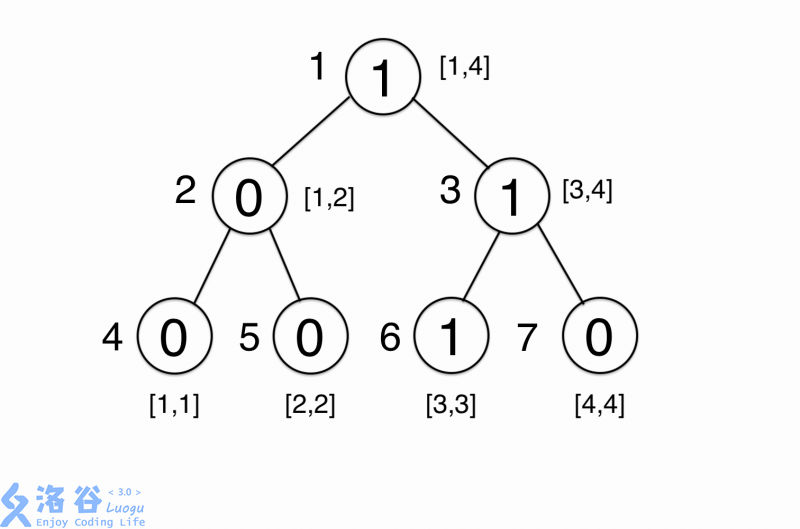
void MakePoint_ (int now,int L,int R,int V){ //求出树上每个节点的权值，V表示在数中插入的元素离散化后的值 
    ++node[now].size; //因为V属于当前区间，所以对应区间的权值加一 
    if (R==L) return; //边界 
    int mid=(L+R)>>1;
    if (V<=mid) MakePoint_ (node[now].left,node[k].left,L,mid,V); //如果V比mid小，那么V属于左子树的区间，向左继续更新权值 
    else MakePoint_ (node[now].right,node[k].right,mid+1,R,V); //否则向右更新权值 
    return;
} 
int getnum_ (int k){  //用二分的思想获取原数组离散化后的值 
    int L=1,R=N;
    while (L<=R){
        int mid=(L+R)>>1;
        if (b[mid]==k) return mid;
        else if (b[mid]>k) R=mid-1;
        else L=mid+1;
    }
    return 0;
}
int main (){
    scanf ("%d",&N); //读取数列个数 
    for (int i=1;i<=N;++i)  //读入数列，a数组为原序列，b数组为离散化的序列 
        scanf ("%d",&a[i]),b[i]=a[i];
    sort (b+1,b+N+1); //将b数组排序，那么原a数组中的最小值对应1，第二小值对应2...
    Build_ (1,N); //先把树的节点编号和左右孩子求出来 
    for (int i=1;i<=N;++i){
        MakePoint_ (1,1,N,getnum_ (a[i])); //将元素一个一个插入树中并更新树上的权值 
    }
    return 0;
}

假设给定一串序列A={3,2,4,1}，那么构建出来的线段树应该是这样的(节点上为当前区间的元素个数，节点旁边分别为节点编号以及维护的区间):

这里维护的是 [1,4] 的区间，那么如果我们要求这个区间的第3大的值，令 L=1 R=4 先将3与根节点的左子树的权值比较，左子树存的是 [1,2] 区间的值的个数为2，因为3>2，所以我们所求值不能在左子树中找(总共只有2个数要求第3大的数再怎么也求不出吧XD)

接着看向右子树，右子树存储的是 [3,4] 区间个元素个数也为2，那么是不是找不到了呢?再想一想，我们应该在右子树找的应该是第3-2=1大的值(这个应该不难理解吧，用所求的第k大的值减去左子树的权值)，因为1<=2，所以继续从右子树向下搜，L变成中间值 (L+R)/2+1 r不变 重复这个过程直到 L=R ，那么此时的 L 为所求的元素离散化后的值

代码如下:

int Query_ (int Tree,int L,int R,int K){  //查询函数 Tree表示当前节点的编号
					                      //L,R表示区间边界 
               					          //K表示需要查询区间[L,R]的第K大元素 
    if (L==R) return L;  //到达边界了，返回L 
    int mid=(L+R)>>1; //求中点的值 
    if (node[node[Tree].left].size>=K) return Query_ (node[Tree].left,L,mid,K); //如果当前节点左子树的值比K大则查询左子树 
    else return Query_ (node[Tree].right,mid+1,R,K-node[node[Tree].left].size); //否则查询右子树 
}

但是这样显然是不够的，我们只能求出 [1,4] 区间的第K大，而题目要求是任意区间，我们总不能对每一种可能的区间都进行建树，因此我们考虑运用前缀和的方法，只需要再建立维护 [1,1] , [1,2] , [1,3] 区间的线段树

例如再建一颗维护 [1,1] 区间的线段树：

为了方便我再把之前那张线段树的图贴出来

我们观察根节点的权值，发现权值差正好是 [2,4] 区间内元素个数，再看其左子树，差为2，那么这个2表示什么呢？再看看原数列， [2,4] 区间元素为{2,4,1}，其中大小(或者说离散化后的编号)在 [1,2] 区间内的元素正好是2个，再对比其他节点的权值，我们可以得出，对于两个分别维护区间 [1,i] 和区间 [1,j] (0<=i<j<=N)的线段树，其对应节点权值之差等于区间 [i+1,j] 中此节点维护的区间内的元素个数

但是对于一个长度为N的序列建立N个线段树也并不现实，因此我们需要继续优化

再看之前的维护 [1,1] 的线段树，若我们插入一个节点，即使其维护区间 [1,2]

这時得到的线段树为：

可以发现，被修改的实际上只有一条链：

继续插入也是一样，只在前一颗树的基础上修改了一条链的权值，因此我们不需要构建那么多个线段树，只需要构建一棵树再在树上增加链就行了，也就成了我们需要的可持久化线段树：

接下来是构建过程：

先建造一个空树

插入第一个节点(红色表示添加部分，为了简便没有注明节点编号与维护区间，而且很小请见谅):

每次新建一条链，并与上一棵树连接(对于每个节点的两个子节点，若该数大小在左子树区间内则新建左子树，左子树先默认与前一颗树当前位置左子树状态相同(状态相同即结构体内的 left,right,size 相同)，然后进行加权值，右子树为前一棵树相同位置的右子树，否则新建右子树)接下来也是一样

此时我们就得到了维护区间 [1,4] 的可持久化线段树，如果以右上权值为4的那个节点为根节点来看，与之前得到维护 [1,4] 的线段树是一样的

因为现在是一颗可持久化线段树，因此操作与之前的也有略微区别，我们先定义一个数组 Root[] Root[i] 表示第 i 条链的根节点，也就是第 i 条线段树，再修改之前的建树以及查询函数:

代码实现:

#include <bits/stdc++.h>
#define RE register
#define IL inline
using namespace std;
struct Tree{
    int left;
    int right； 
    int size;
}node[5000001];  //用结构体存树节点的左孩子，右孩子和当前的权值 
int tot_,a[5000001],b[5000001],N,M,Root_[5000001],Q;
IL int Build_ (int L,int R){
	int now=++tot_; //now为当前节点编号 
    int mid=(L+R)>>1; //获取区间中点 
    if (L!=R){ //边界 
    node[now].left=Build_ (L,mid); //向左建树 
    node[now].right=Build_ (mid+1,R); //向右建树 
	}
    return now;
}
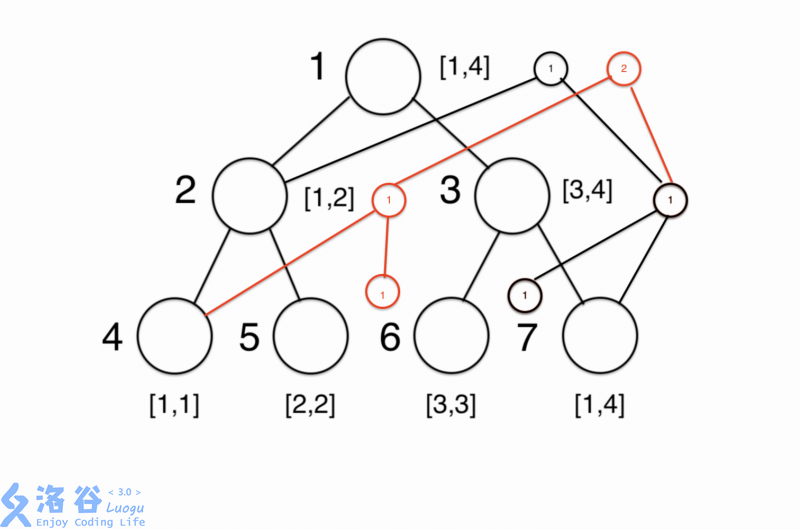
IL int MakePoint (int before,int L,int R,int V){ //新增一条链，V表示在数中插入的元素离散化后的值
	int now=++tot_; 
	node[now]=node[before]; //先将当前新增的节点连向前一棵树相同位置的左右子树，同时权值也与前一棵树相同位置相同 
    ++node[now].size; //因为V属于当前区间，所以对应区间的权值加一 
    if (R!=L){//边界 
    int mid=(L+R)>>1;
    if (V<=mid) node[now].left=MakePoint_ (node[before].left,L,mid,V); //如果V比mid小，那么V属于左子树的区间，新建一个左节点 
													 				   //因为没有右子树没有任何更改，也就不需要建节点
													 				   //因为之前已经将当前位置的右子树修改为前一棵树当前位置的右子树
																	   //所以不需要进行任何修改 
    else node[now].right=MakePoint_ (node[before].right,mid+1,R,V);    //否则新建右子树 
	} 
    return now;
}
IL int Query_ (int TreeA,int TreeB,int L,int R,int K){  //查询区间[A+1,B]也就是查询第A棵树和第B棵树 
										  		   	    //L,R表示区间边界 
										 			    //K表示需要查询区间的第K大元素 
    if (L==R) return L;  //到达边界了，返回L 
    int mid=(L+R)>>1; //求中点的值 
    int x=node[node[TreeB].left].size-node[node[TreeA].left].size; //计算两棵树相同位置的左子树的权值差
																   //即区间[A+1,B]中大小区间位于[L,R]的元素个数 
    if (x>=K) return Query_ (node[TreeA].left,node[TreeB].left,L,mid,K); //若这个个数比K大，则第K大在[L,mid]区间内
																		 //也就是当前节点左子树维护的区间 
    else return Query_ (node[TreeA].right,node[TreeB].right,mid+1,R,K-x); //否则向右查询 
}
IL int getnum_ (int k){  //用二分的思想获取原数组离散化后的值 
    int L=1,R=N;
    while (L<=R){
        int mid=(L+R)>>1;
        if (b[mid]==k) return mid;
        else if (b[mid]>k) R=mid-1;
        else L=mid+1;
    }
    return o;
}
int main (){
    scanf ("%d %d",&N,&Q); //读取数列个数和查询个数 
    for (RE int i=1;i<=N;++i)  //读入数列，a数组为原序列，b数组为离散化的序列 
        scanf ("%d",&a[i]),b[i]=a[i];
    sort (b+1,b+N+1); //将b数组排序，那么原a数组中的最小值对应1，第二小值对应2...
    M=unique (b+1,b+N+1)-(b+1); //将数据去重，因为求第K大我们不需要重复的一样大小的元素
    Root_[0]=++tot_; //0号线段树的根节点为1 
    Build_ (1,M); //建立最初始的树，也就是维护区间[0,0]的树 
    for (RE int i=1;i<=N;++i){
        Root_[i]=MakePoint_ (Root_[i-1],1,M,getnum_ (a[i])); //将元素一个一个插入树中并更新树上的权值， 
    }
    for（RE int i=1;i<=Q;++i）{
    	int x,y,k; //查询[x,y]区间第k大 
    	scanf ("%d %d %d",&x,&y,&k);
    	printf ("%d\n",b[Query_ (Root_[x-1],Root_ [y],1,M,k)]); //也就是查询第x-1和第y棵树
																//查询函数返回的是序列第K大在原数列的大小位置
																//因此要输出其在排序后的数组b中对应的值 
	}
    return o;
}

接下来看一下第二道板子题，题目要求对历史版本进行修改与查询，再看一下上一题中我们建的树:

单独看最上面一排的五个节点，其实可以发现以每个节点为根形成的线段树都是一个历史版本(这个历史就是我们按数列插入节点)，那么对于这一题，我们不需要维护区间值个数，只需要在叶节点插入对应位置的值即可，然后对于每次修改，有影响的也只有对应位置的一个值，我们也只需要构建一条链，所以大体思路是和上一题一样的，直接上代码吧:

#include <bits/stdc++.h>
#define LL long long
#define RE register
#define IL inline
using namespace std;
struct tree{ //这里和前面一样用结构体存树
	LL right;
	LL left;
	LL size;
}node[1000001];
LL tot_,Root_[1000001],N,M,a[1000001];
IL LL Build_ (LL L,LL R){ //初始建树也差不多
	LL now=++tot_;
	if (L==R){
		node[now].size=a[L]; //如果L=R即当前区间已经到最小，树也建到了叶节点
                             //将叶子节点的值更新为对应数组的值
	}
	else{
		LL mid=(L+R)>>1;
		node[now].left=Build_ (L,mid);
		node[now].right=Build_ (mid+1,R);
	}
	return now;
}
IL LL MakePoint_ (LL Tree,LL L,LL R,LL I,LL K){ //建造一条链，思路 也是一样
	LL now=++tot_;
	node[now]=node[Tree];
	if (L==R){
		node[now].size=K;   //到达边界则修改当前位置的节点
		return now;
	}
	LL mid=(L+R)>>1;
	if (I<=mid) node[now].left=MakePoint_ (node[Tree].left,L,mid,I,K); //如果需要修改的节点位置小于mid
                                                                       //则新建左子树
	else node[now].right=MakePoint_ (node[Tree].right,mid+1,R,I,K);    //否则新建右子树
	return now;
}
IL LL Qurey_ (LL Tree,LL L,LL R,LL K){
	if (L==R) return node[Tree].size;               //查询時只要返回对应位置的权值即可
	LL mid=(L+R)>>1;
	if (mid>=K) return Qurey_ (node[Tree].left,L,mid,K);
	else return Qurey_ (node[Tree].right,mid+1,R,K);
}
int main (){
	scanf ("%lld %lld",&N,&M);
	for (RE int i=1;i<=N;++i)
		scanf ("%lld",&a[i]);
	Root_[0]=Build_ (1,N);
	for (RE int i=1;i<=M;++i){
		LL x,OP,y,z;
		scanf ("%lld %lld %lld",&x,&OP,&y);
		if (OP==1){
			scanf ("%lld",&z),Root_[i]=MakePoint_ (Root_[x],1,N,y,z); //这一次是再第x的版本上新建链而不是i-1，同时注意新建版本
		}
		else{
			Root_[i]=Root_[x]; //查询也算要建一次新版本
			printf ("%lld\n",Qurey_ (Root_[i],1,N,y)); //查询
		}
	}
	return 0;	
}

那么大概就这样吧，我也不清楚还要讲些什么了，总之我认为可持久化线段树的思路就是通过以建链代替建树达到建立历史版本的需求，因为有大量的重复节点，这样可以节省空间和时间。总之就这样了，我还只会写模板，还不会具体的应用，这篇文章如果有什么问题欢迎大佬指出。。。

可持久化线段树学习笔记

原文：https://www.cnblogs.com/IQZ-HUCSr-TOE/p/12631101.html