时间复杂度

这篇文章并不会讲时间复杂度的理论知识，而是通过讨论分析几种经典的时间复杂度，从而使我们能够求解平常开发中遇到的代码的时间复杂度。

时间复杂度分析方法：

1、循环执行次数最多的代码

int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

这段代码执行次数最多的就是第4、5行代码。这段代码的时间复杂度取决于第4、5行的时间复杂度，因此这段代码的时间复杂为 O(n)。

2、加法法则：总复杂度等于量级最大的那段代码的时间复杂度

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }
 
   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1; 
     for (; j <= n; ++j) {
       sum_3 = sum_3 +  i * j;
     }
   }
 
   return sum_1 + sum_2 + sum_3;
 }

这段代码中sum_1求和的那段代码的时间复杂度为 O(1),sum_2求和的那段代码的时间复杂度为 O(n),sum_3求和的那段代码的时间复杂度为 O(\(n^2\))。

量级最大的是求解sum_3的那段代码。因此这整段代码的时间复杂度取决于sum_3那段代码，所以整段代码的时间复杂度为 O(\(n^2\))。

3、乘法法则：嵌套代码的时间复杂度等于嵌套内外代码复杂度的乘积

int cal(int n) {
   int ret = 0; 
   int i = 1;
   for (; i < n; ++i) {
     ret = ret + f(i);
   } 
 } 
 
 int f(int n) {
  int sum = 0;
  int i = 1;
  for (; i < n; ++i) {
    sum = sum + i;
  } 
  return sum;
 }

这里单独看 cal 函数的时间复杂度为 O(n),但是 cal 函数调用的 f 函数的时间复杂度也是 O(n)。

因此这一整段代码的时间复杂度等于 O(n) * O(n) -> O(\(n^2\))。

几种常见的时间复杂度(按数量级递增)：

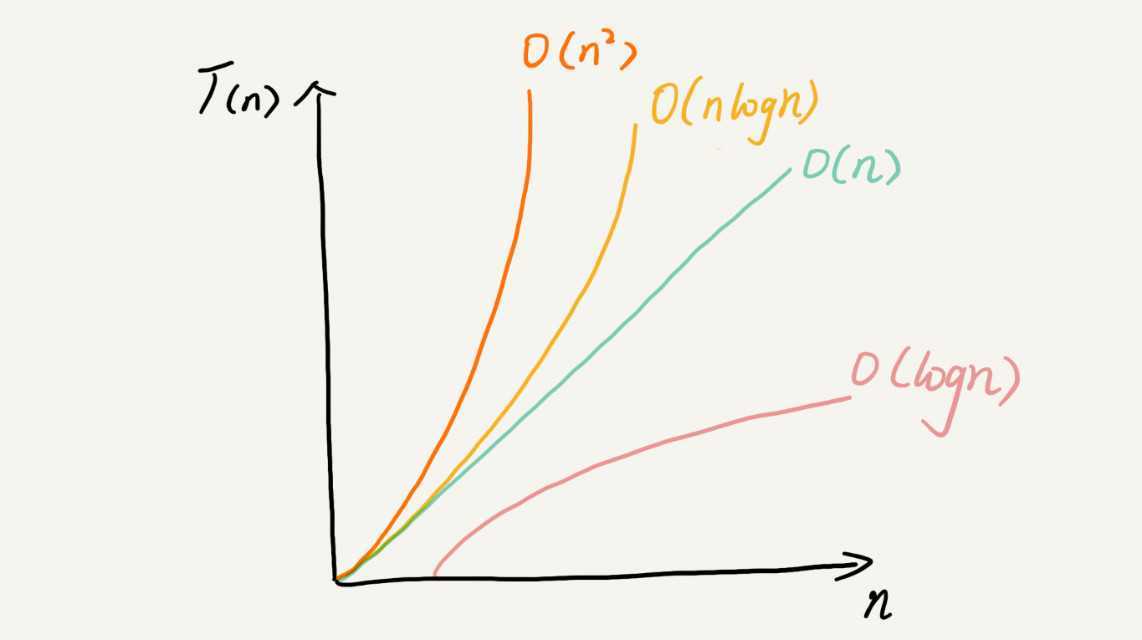
1、常量阶 O(1)

2、对数阶 O(logn)

3、线性阶 O(n)

4、线性对数阶 O(nlogn)

5、平方阶 (\(n^2\))、立方阶(\(n^3\))....k次方阶(\(n^k\))

6、指数阶 (\(2^n\))

7、阶乘阶 (n!)

几种经典的时间复杂度

1、O(1)

只要代码的执行时间不随着 n 的增大而增大，一般时间复杂度都为 O(1)。或者说只要代码中不含有循环、递归，即使是成千上万行的代码，那么时间复杂度也是 O(1)。

int i = 0;
int j = 1;
System.out.println(i + j);

2、O(logn) 和 O(nlogn)

for(int i = 1;i < n;i = i*2){
    System.out.println(i);
}

这里我们可以发现 i 的取值规律就是等比数列：

所以只要能求出 x 的值就知道循环的次数了。

\(2^x = n\)

\(x = log_2 n\)

以此类推出，以下代码的时间复杂度就是 \(x = log_3 n\)。

for(int i = 1;i < n;i = i*3){
    System.out.println(i);
}

理解了 O(logn) 这种时间复杂度之后 O(nlogn) 这种时间复杂度就不难理解了。利用前面我们讲的乘法法则，只要 O(logn) 循环运行 n 次，那么时间复杂度就是O(nlogn)。

3、O(n)

for (int = 1; i<=n; i++) {
 System.out.println(i);
}

4、O(\(n^2\))

for (int i = 1; i <= n; i++) {
 for (int j = 1; j <=n; j++) {
 System.out.println(i + " and " + j);
 }
}

5、O(\(2^n\))

for (int i = 1; i <= Math.pow(2, n); i++){
 System.out.println(i);
}

6、O(n!)

for (int i = 1; i <= factorial(n); i++){
 System.out.println(i);
}

6、O(n + m) 和 O(n * m)

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

因为在这里我们无法比较m和n的大小，所以之前的加法法则就不能再使用了。

这里需要对加法法则进行改进T1(m) + T2(n) = O(f(m) + g(n))。

所以这段代码的时间复杂度为 O(n + m)。乘法法则也适用 T1(m) * T2(n) = O(f(m) * g(n))。

各种时间复杂度的坐标图

欢迎关注个人公众号，可直接扫描以下二维码或微信搜索“阿毛聊技术”。

时间复杂度

原文：https://www.cnblogs.com/limaodeng/p/12624807.html