算法是什么?
算法是用于解决特定问题的一系列执行步骤,例如简单一个求和公式,也是算法,但是不同的算法,解决同一个问题,效率可能相差非常大。
斐波那契数是什么?
前面两个数的和是下一个数的值。例如:0 1 1 2 3 5 8 13...
1 package com.mj; 2 3 public class Main { 4 /* 1 2 3 4 5 6 这一排代表要求第n项 5 * 0 1 2 3 4 5 这一排代表要计算多少次 6 * 0 1 1 2 3 5 8 13...这一排是斐波那结果 7 * 8 * */ 9 //第一个int是返回值 第二个int是入参类型 10 public static int fib(int n) { 11 //传入的n代表是要取第几位斐波那契数 小于等于1 没必要计算 直接返回 12 if(n <= 1) return n; 13 //能进来这一步 n肯定大于1 假设0是第一位 1是第二位 14 int first = 0; 15 int second = 1; 16 //需要计算n-1次 17 for (int i = 0; i < n - 1; i++) { 18 int sum = first + second; 19 //相加的和会变成下一项 第二位数 20 //原先第二位数变成待相加的第一位数 21 first = second; 22 second = sum; 23 } 24 //最后返回结果 25 return second; 26 } 27 public static void main(String[] args) { 28 System.out.print(fib(30)); 29 30 } 31 }
判断算法的好坏
1.准确性(保证算法是正确的)
可读性(易读)
健壮性(异常处理)
2.时间复杂度:估算程序指令的执行次数。(执行时间)看要执行多少条指令
举个例子
1 //int i = 0 执行1次 2 //i < n 执行n次 3 //i++ 执行n次 4 //打印 执行n次 5 //结果1+3n 6 for (int i = 0; i < n; i++) { 7 System.out.print(i); 8 }
public static void test(int n) { //n除以2再赋值给n 就是看n除几次还能大于0 //例如n = 8 //8/2 = 4 4/2 = 2 2/2 = 1 就是三次 其实就是2^3次方 求对数 //执行次数=log2(n) 除以几 就是求几的对数 while ((n = n / 2) > 0) { System.out.println("test"); } }
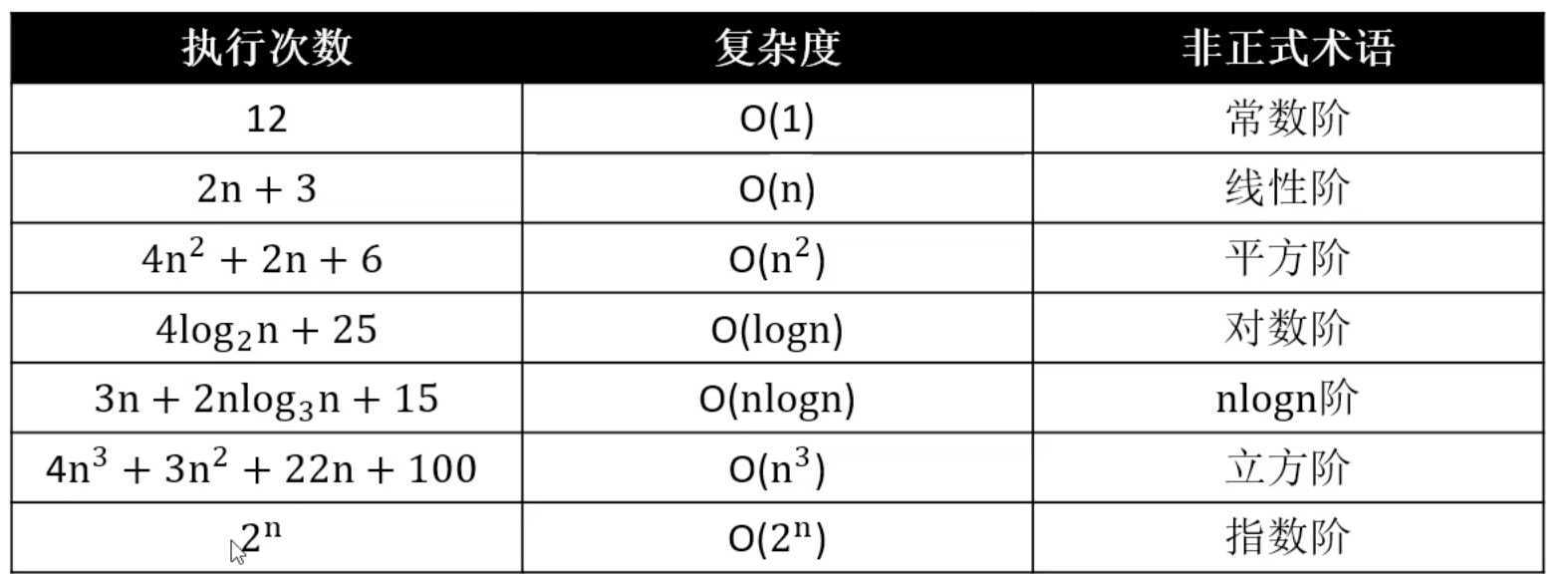
大O表示法:O的意思是估算
1.时间复杂度
忽略常数:时间复杂度的结果是常数的话 意思就是遍历次数是有限的 不为n 统一为O(1)
如果复杂度是2n+3 这类 忽略2和3的常数 就是O(n)
有高阶的n^2+2n+6 就忽略低阶的2n和常数6 结果O(n^2)
更高阶的4n^3+3n^2+22n+6 结果O(n^3)
对数 结果是O(logn) log2n = log2^9 *log9^n

2.空间复杂度。(整个算法开辟了多少内存)
public static void test1(int n) {
//只开辟了int变量一次 for (int i = 0; i < n; i++) { System.out.println(111); } }
空间复杂度是O(1)
int[] array = new int[n];//O(n)
现在设备的内存都比较大 可能更多的考虑时间复杂度
原文:https://www.cnblogs.com/WellLin/p/12633790.html