【形式语言和自动机】DFA和NFA

参考博客 https://www.cnblogs.com/AndyEvans/p/10240790.html

本节知识点是《编译原理》第三章-词法分析，学习参考教材为清华大学出版社《编译原理》第三版：

前情提要：

字母表∑1和∑2的乘积( product)：

　　∑1∑2 ={ab|a ∈∑1, b ∈ ∑2}

　　例： {0, 1} {a, b} ={0a, 0b, 1a, 1b}

字母表∑的n次幂( power)：长度为n的符号串构成的集合

　　∑0 ={ ε }
　　∑n =∑n-1 ∑ , n ≥

　　例： {0, 1}3 ={0, 1} {0, 1} {0, 1}={000, 001, 010, 011, 100, 101, 110, 111}

字母表的正闭包（positive closure）：长度正数的符号串构成的集合：

　　∑+ = ∑ ∪∑2 ∪∑3 ∪…

　　例：{a, b, c, d }+ = {a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}

字母表的闭包（Kleene closure）：任意符号串（长度可以为零）构成的集合：

　　∑* = ∑0 ∪∑+ = ∑0 ∪∑ ∪∑2 ∪∑3 ∪…

　　例：{a, b, c, d }* = {ε, a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}

一、【 有穷自动机 】：

1、定义

有穷自动机 ( Finite Automata，FA )

具有一系列离散的输入输出信息和有穷数目的内部状态（状态：概括了对过去输入信息处理的状况）

2、FiniteAutomata的表示：

转换图 (Transition Graph)
　　结点：FA的状态
　　初始状态（开始状态）：只有一个，由start箭头指向
　　终止状态（接收状态）：可以有多个，用双圈表示
　　带标记的有向边：如果对于输入a，存在一个从状态p到状态q的转换，就在p、q之间画一条有向边，并标记上a

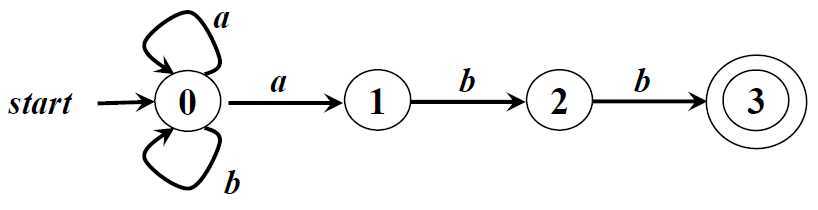
3、Finite Automata定义(接收)的语言

给定输入串x，如果存在一个对应于串x的从初始状态到某个终止状态的转换序列，则称串x被该FA接收
由一个有穷自动机M接收的所有串构成的集合A称为是该FA定义（或接收）的语言，记为A=L(M （machine）)

We say that M recognizes A.

A machine may accept several strings, but it always recognizes only one language.

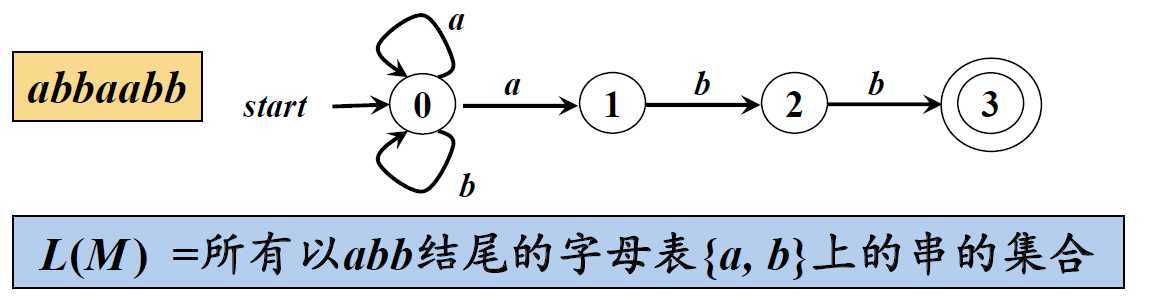
4、最长子串匹配原则(Longest String Matching Principle )

·当输入串的多个前缀与一个或多个模式匹配时，总是选择最长的前缀进行匹配

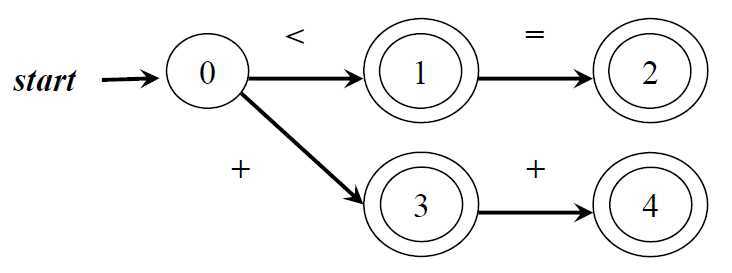
·在到达某个终态之后，只要输入带上还有符号， DFA就继续前进，以便寻找尽可能长的匹配

二、【 有穷自动机的分类 】：

　确定的FA (Deterministic finite automata, DFA)
　非确定的FA (Nondeterministic finite automata, NFA)

1、确定的有穷自动机DFA(Deterministic Finite Automata)

定义： (DFA (确定型有穷自动机)) A deterministic ?nite automaton (DFA) is a 5-tuple (Q,Σ,δ,q0,F)

where

1 Q is a finite set called the states,

2 Σ is a finite set called the alphabet,

3 δ : Q×Σ → Q is the transition function,

4 q0 ∈ Q is the start state，

5 F ⊆ Q is the set of accept states.
例子

 注意F是集合

用转换表表示DFA

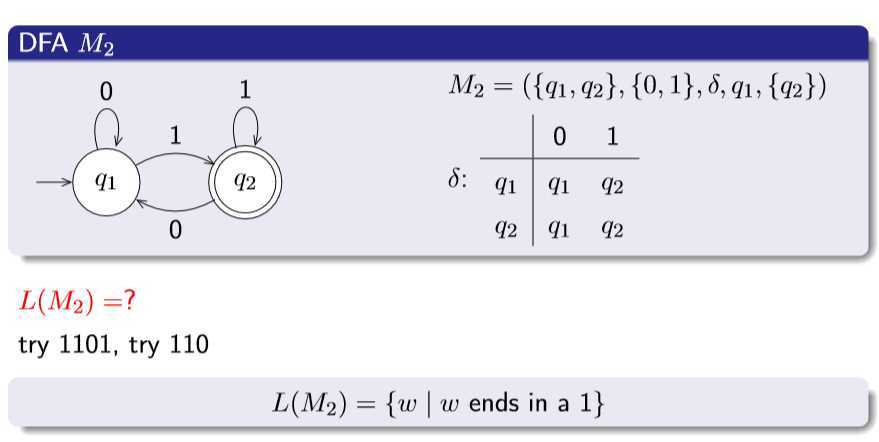
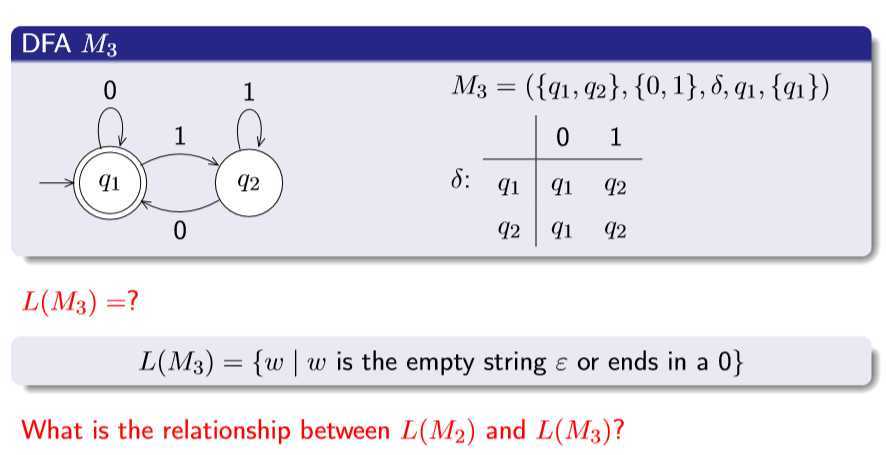
 M2和M3，两个互为补集。Σ*=L(M2)+L(M3)

求一个自动机的补集：把终结状态和非终结状态互换

2、非确定的有穷自动机NFA(NonDeterministic Finite Automata)

定义 (NFA) A nondeterministic ?nite automaton (NFA) is a 5-tuple (Q,Σ,δ,q0,F)

where

1 Q is a ?nite set of states, 有穷状态集

2 Σ is a ?nite alphabet,  输入符号集合，即输入字母表。假设ε不是Σ中的元素

3 δ : Q×Σε →P(Q) is the transition function,

4 q0 ∈ Q is the start state,

5 F ⊆ Q is the set of accept states.

P(Q) is the power set of Q

Σε = Σ∪{ε}

例子：

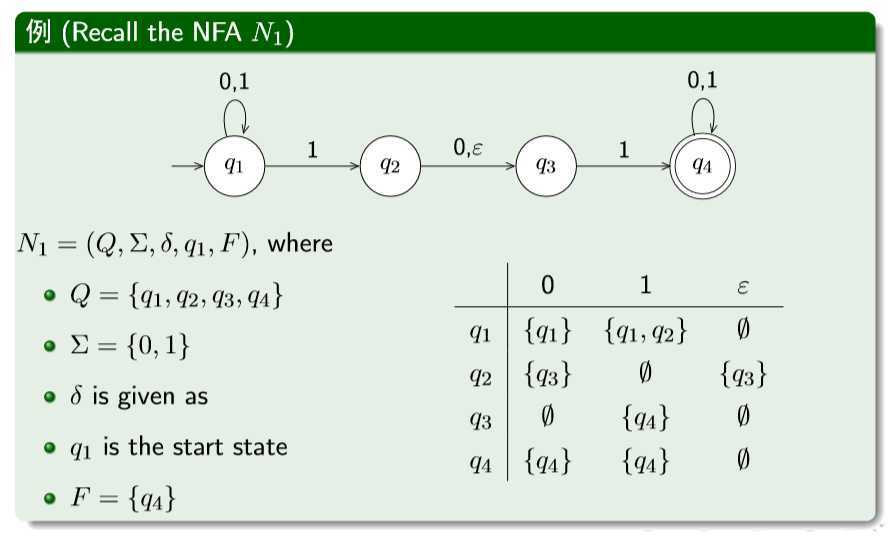
三、【 从正则表达式到有穷自动机 】

ε对应的NFA

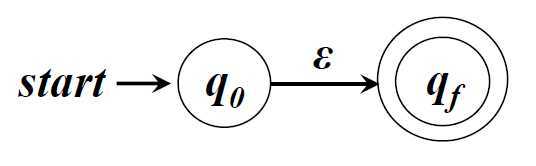
□ 字母表Σ中符号a对应的NFA

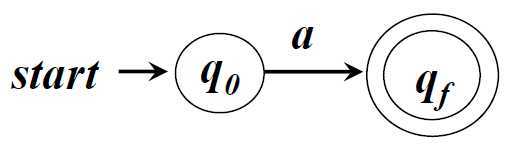
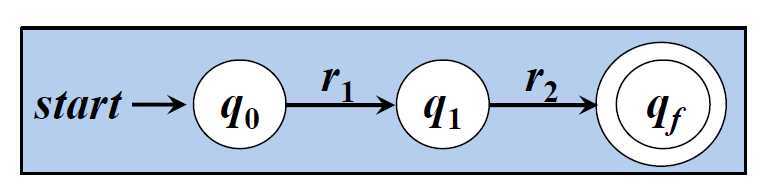
□ r = r₁r₂对应的NFA

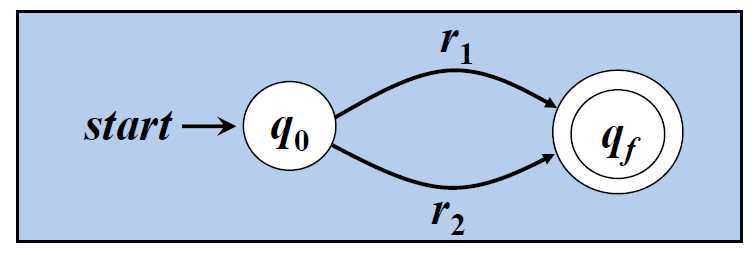
□ r = r₁|r₂对应的NFA

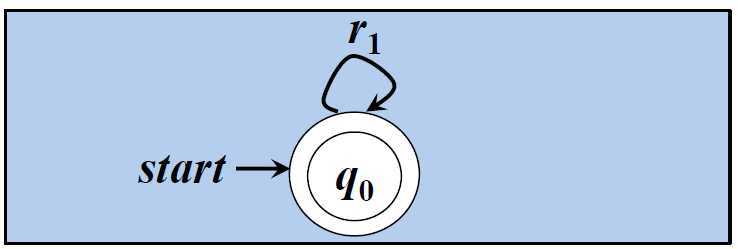
□ r = (r₁)*对应的NFA

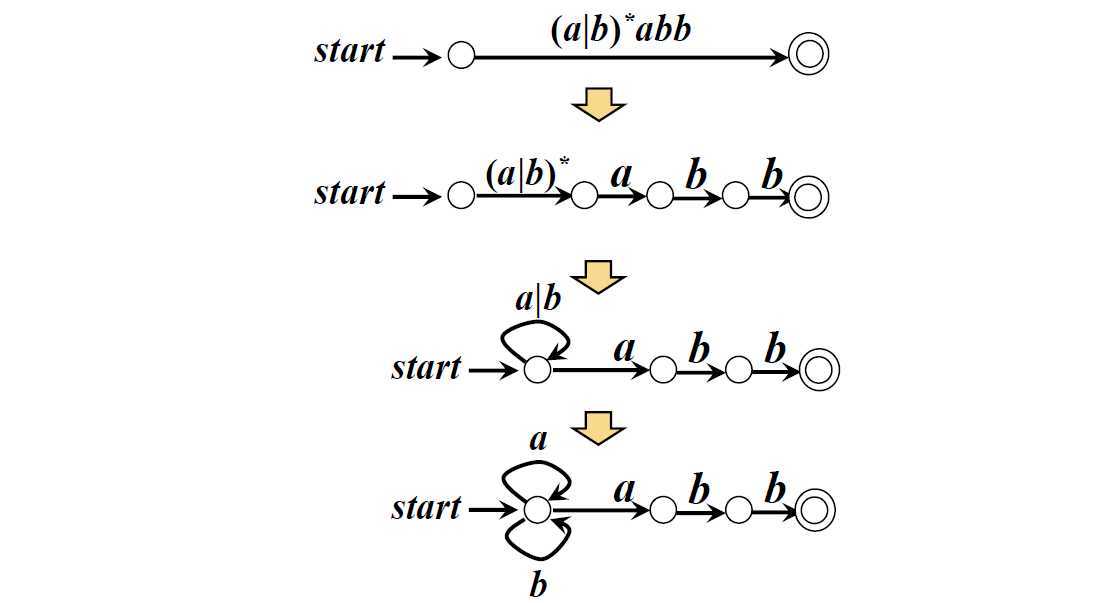
例:r=(a|b)*abb 对应的NFA

【形式语言和自动机】DFA和NFA

原文：https://www.cnblogs.com/conver/p/12635437.html