就在土匀匀还在准备联赛的时候，学霸
已经拿到了金牌。于是，开心的学霸用他的笔记本玩起了足球联盟。
足球联盟里有 \(n\) 只球队，编号为 \(1\)~\(n\)，的球队编号为 \(n\)。现在联赛已经进行了很多轮，每个球队都有了一定的积分。
聪明的通过对游戏源代码的分析，得到了接下来的所有赛程。
想，如果他可以控制所有剩下比赛的结果的话，能否使得他的球队获得比其他所有球队都更高的分数。
积分的规则是：对于一场比赛，赢的球队得 \(2\) 分，输的球队得 \(0\) 分，如果是平局，两支球队各得 \(1\) 分。
第一行为一个整数 \(T\)，表示数据组数。对于每组数据：
第一行为两个正整数 \(n\) 和 \(m\)，表示球队的数目和剩余比赛的数目。
第二行为 \(n\) 个非负整数，表示每个球队现在的积分，不超过 \(1000\)。
接下来 \(m\) 行，每行两个整数 \(x\)、\(y\)，表示球队 \(x\) 和球队 \(y\) 之间有一场比赛。
每组数据一行，如果能使自己的球队获得最高的分数（没有并列），输出 YES，否则输出 NO。
测试时间限制 \(1000\ \mathrm{ms}\)，空间限制 \(256\ \mathrm{MiB}\)。
这道题是一道很有意思的题。要根据题中的限制来选择算法。
我们就假设那个人是 A 君。
枚举每一种比赛的胜负情况，再暴力算出来。
复杂度：\(\Theta(3^mn)\)。
我们有必要想一下，有什么结论可以使用。
这是显然的，这样可以尽可能让 A 君的球队得分。
这也是显然的，因为赢的分数太多了就可能导致 A 君的球队落选。
但是，对于剩下的球队，我们难以指控。我们应该抽象一下这道题。
首先，有若干个数，每个数都有一个初始值。
接下来，我们有若干个操作，可以将其中两个数分别加上 \(a,b\)，要求 \(a,b\in \mathbb{N}\) 且 \(a+b=2\)
最后，我们要知道，是否存在一种操作，使完成所有操作后每个数都小于一个给定的数。
当然，如果我们换一种表述，你就有可能发现这道题的正解：
有若干个水罐，每一个水罐都有一个固定容积，初始时为空。我们有若干个倒水措施，使得其中两个水罐里加起来能够倒入 \(2\) 单位的水。
最后，我们想要知道，是否存在一个倒水操作，使得所有的水罐都不会溢出。
没错，我们可以利用网络流来解决这个问题。
图可以这样设计：
画出来就是这个样子：
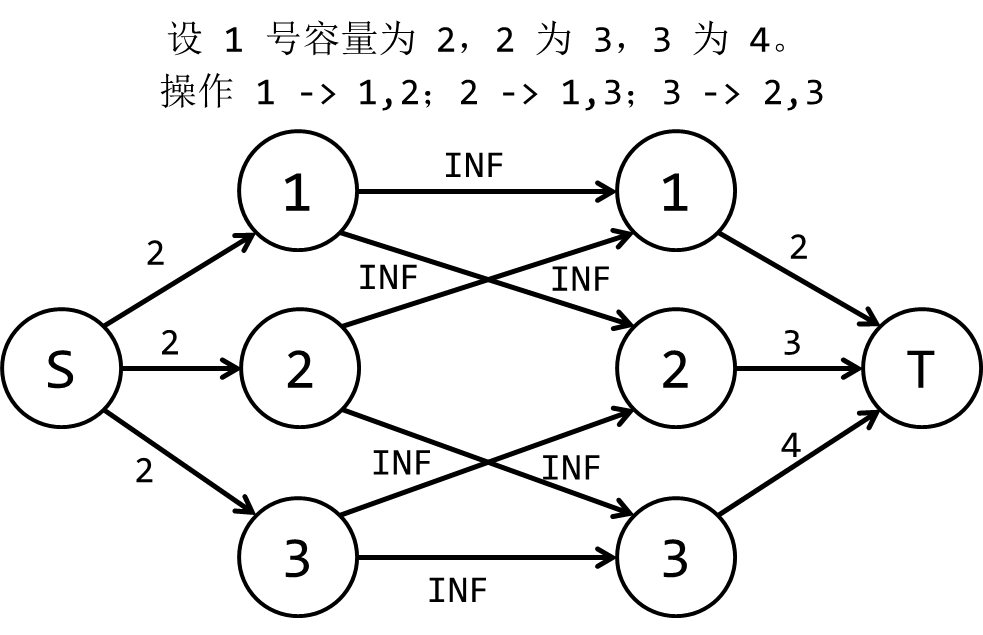
对应到这题上来，每一个球队的“容量”实际上就是能赢多少分，却不会超过 A 君的球队。
就是 A 君球队的分数减去对应球队分数再减一。
如果最后跑出来的最大流已经是 S 的满流，那么就是可以出线的。反之同理。
这样，图的复杂度是 \(\Theta(n+m)\)，再跑一遍网络流，复杂度就是 \(\mathcal{O}((n+m)^3)\)，基本跑不满，可以通过本题。
（这里的复杂度是以基本 ISAP 计算，如果用 HLPP 或者 LCT 优化 ISAP 还能更快。）
又是又臭又长的代码，但是核心还是很短的。
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
using namespace std;
const int max_n = 100, max_m = 1000, max_node = max_n + max_m + 1, max_edge = max_m * 3 + max_n, INF = 0x3f3f3f3f;
int hd[max_node], des[max_edge<<1], val[max_edge<<1], occ[max_edge<<1], nxt[max_edge<<1], edge_cnt = 0;
int hei[max_node], gap[max_node], cur[max_node], sco[max_n];
bool flag;
queue<int> q;
inline int nid(int id) { return max_m + 1 + id; }
inline int my_min(int a, int b) { return (a < b)? a:b; }
inline int read()
{
int ch = getchar(), n = 0, t = 1;
while (isspace(ch)) { ch = getchar(); }
if (ch == ‘-‘) { t = -1, ch = getchar(); }
while (isdigit(ch)) { n = n * 10 + ch - ‘0‘, ch = getchar(); }
return n * t;
}
void _a(int s, int t, int v)
{
des[edge_cnt] = t, val[edge_cnt] = v;
nxt[edge_cnt] = hd[s], hd[s] = edge_cnt++;
}
void add_edge(int s, int t, int v)
{
_a(s, t, v);
_a(t, s, 0);
}
int aug(int s, int t, int lim)
{
if (s == t)
return lim;
if (!flag)
return 0;
int tmp, flow = 0;
for (int& p = cur[s]; p != -1; p = nxt[p])
if (hei[des[p]] == hei[s] - 1)
{
tmp = aug(des[p], t, my_min(lim, val[p] - occ[p]));
flow += tmp, occ[p] += tmp, occ[p^1] -= tmp, lim -= tmp;
if (lim <= 0)
return flow;
}
gap[hei[s]]--, cur[s] = hd[s];
if (!gap[hei[s]])
flag = false;
hei[s]++, gap[hei[s]]++;
return flow;
}
int main()
{
int cas = read(), n, m, ta, tb, rcnt;
bool over;
while (cas--)
{
memset(hd, -1, sizeof(hd));
memset(hei, -1, sizeof(hei));
memset(gap, 0, sizeof(gap));
memset(occ, 0, sizeof(occ));
edge_cnt = 0, over = false, flag = true, rcnt = 0;
n = read(), m = read();
for (int i = 0; i < n; i++)
sco[i] = read();
for (int i = 0; i < m; i++)
{
ta = read() - 1, tb = read() - 1;
if (ta == n - 1 || tb == n - 1)
sco[n-1] += 2;
else
{
rcnt++;
add_edge(0, rcnt, 2);
add_edge(rcnt, nid(ta), INF);
add_edge(rcnt, nid(tb), INF);
}
}
for (int i = 0; i < n - 1; i++)
{
if (sco[n-1] - sco[i] - 1 < 0)
{
puts("NO");
over = true;
break;
}
add_edge(nid(i), max_node - 1, sco[n-1] - sco[i] - 1);
}
if (over)
continue;
for (int i = 0; i < max_node; i++)
cur[i] = hd[i];
hei[max_node-1] = 0, gap[0] = 1;
q.push(max_node - 1);
while (!q.empty())
{
ta = q.front();
q.pop();
for (int p = hd[ta]; p != -1; p = nxt[p])
if (hei[des[p]] == -1)
{
hei[des[p]] = hei[ta] + 1;
gap[hei[des[p]]]++;
q.push(des[p]);
}
}
ta = 0;
while (flag)
ta += aug(0, max_node - 1, INF);
if (ta == rcnt * 2)
puts("YES");
else
puts("NO");
}
return 0;
}
当时考场上做这道题时，第一感觉居然是 DP。后来才发现是网络流。
看来，这类图论建模的题还要多多练习啊……
原文：https://www.cnblogs.com/5ab-juruo/p/solution-20200328-league.html