我竟然会了如此高深的算法的皮毛
根据众多神犇的 blog 所说,学习 AC 自动机前要学习两个东西:
既然我们都已经会了以上两个数据结构/算法,为什么不进一步学习呢?
现在开始进入正题。
首先我们要知道 AC 自动机使用来干什么的。
一定要记住:这不是一个可以自动帮你 AC 题目的算法。(如有需要请搜索“自动 AC 机”)
那么为什么叫 AC 自动机呢,以下来自某度某科:
Aho-Corasick automation,该算法在1975年产生于贝尔实验室,是著名的多模匹配算法。
好的,这是一个多模匹配算法,那么什么是多模匹配呢?
首先我们知道 KMP 是一种高效的单模匹配算法,就是说从一个文本串中找到一个模式串的所在位置。
那么 AC 自动机就是用来求解:从一个文本串中找到多个模式串的所在位置。
当然,最直接的方法是 暴力 或者 多次KMP,但是复杂度无疑都会爆炸,所以就有了这个高效的多模匹配算法。
首先,我们要输入 \(N\) 个模式串,举个栗子:hit,her,his,she。首先建立一棵 trie 树。
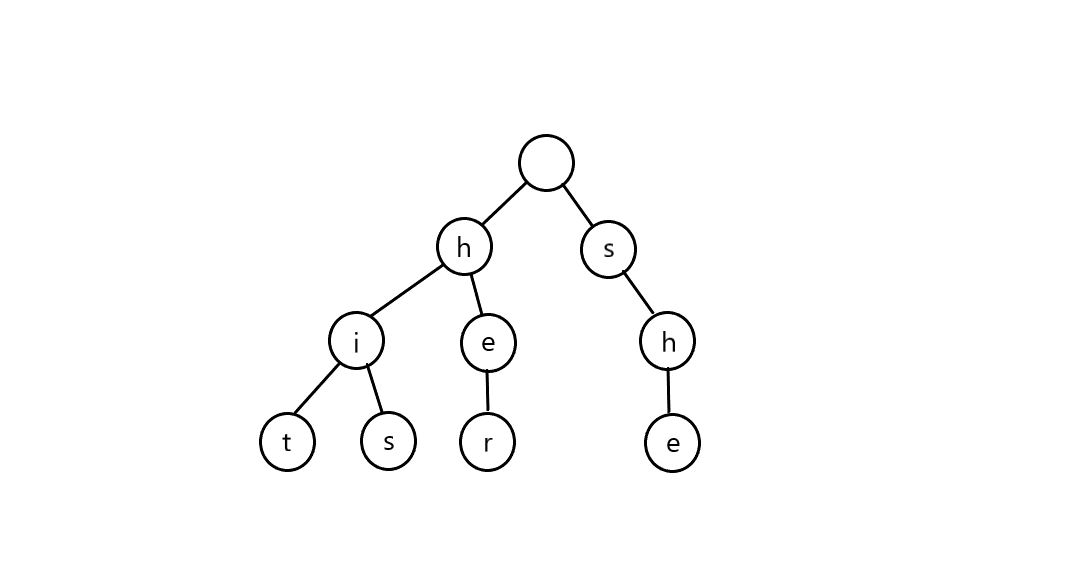
就是酱紫的啦。
然后 ... 。我们来一个神奇的操作:
\(fail\) 是失配指针,注意是失配意味着如果此时匹配失败,那么我们就要到达这个指针指向的位置继续常数匹配。
所以,我们可以将失配指针指向的的节点理解为:
当前节点所代表的串,最长的、能与后缀匹配的,在 trie 中出现过的前缀所代表的节点。
所以,\(fail\) 指针类似于 KMP 的 \(next[]\) 数组,只不过由单串变为了多串而已。
加入失配指针后就是酱紫:
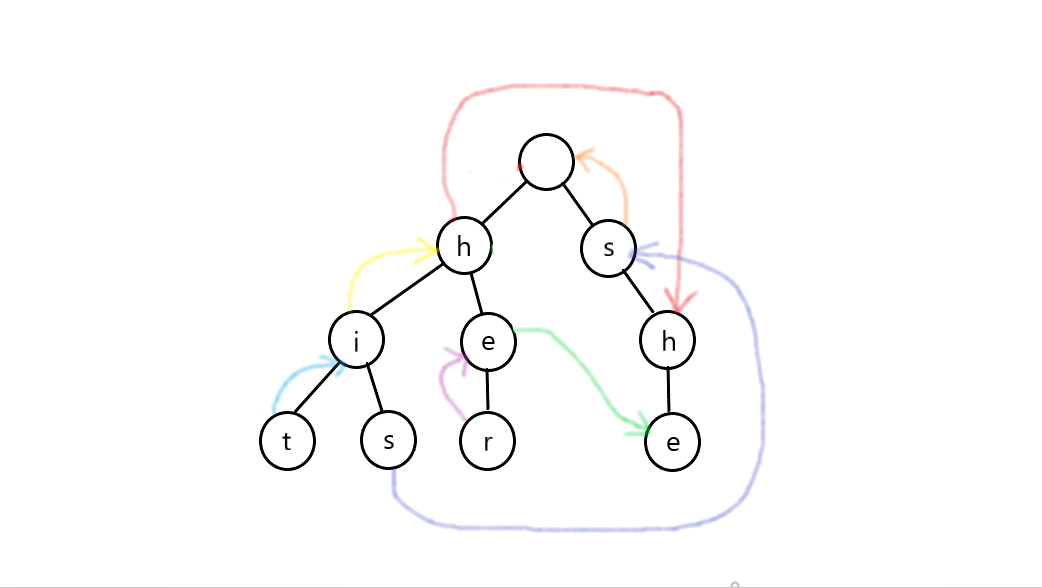
看起来很乱但是很有用的啦,虽然画在了这里但是并不知道怎么求对不对。
我们先看看这个指针是要干什么吧。
每次沿着 Trie 树匹配,匹配到当前位置没有匹配上时,直接跳转到失配指针所指向的位置继续进行匹配。
然后 dalao 们的 blog 告诉我们 Trie 树的失配指针是:
指向沿着其父节点 的 失配指针,一直向上,直到找到拥有当前这个字母的子节点 的节点 的那个子节点。
看不懂?那就继续往下看吧。
简单说就是在 trie 树上跑 KMP,那么显然最难的地方就是找失配指针。(就是上面那个五颜六色的东东)
如果您确保已经理解了 KMP 的 \(next[]\) 数组的含义的话,这就很好理解了。
这就是在失配之后应该去的地方,也因为有这个数组的存在,才让 AC 自动机有了如此高的效率。
这个只能意会而不可言传,理解起来比较难,强烈推荐读者自行画图理解。(或借助上图理解)
然后是匹配,其实匹配的过程十分简单,直接讲述一下即可首先。
指针指向根节点依次读入单词,检查是否存在这个子节点。
然后指针跳转到子节点,如果不存在,直接跳转到失配指针即可。
是不是感觉和 KMP 好像的样子。
显示模板式的 trie 插入:
void insert(string s){
int p=1,len=s.length();
for(int i=0;i<len;i++){
int ch=s[i]-‘a‘;
if(!trie[p][ch]) trie[p][ch]=++tot;
p=trie[p][ch];
}
sum[p]++;//注意一下可能有重复串。
return;
}
然后是最重要的 \(get\_fail()\) 函数,详情请见注释:
void get_fail(){
queue<int>q;
for(int i=0;i<26;i++){//第二层的fail指针提前处理一下。
if(!trie[1][i]) continue;
q.push(trie[1][i]);//加入队列,进行 BFS。
fail[trie[1][i]]=1;//将第二层的 fail 指针指向根节点。
}
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=0;i<26;i++){//枚举所有子节点。
if(trie[now][i]){//存在这个子节点。
fail[trie[now][i]]=trie[fail[now]][i];
//子节点的 fail 指针指向当前节点的。
//fail 指针所指向的节点的相同子节点。
q.push(trie[now][i]);//入队。
}
else trie[now][i]=trie[fail[now]][i];//不存在这个子节点。
//当前节点的这个子节点指向当前节点 fail 指针的这个子节点。
//唯一变化是没有入队。(根本不存在为什么要 BFS 对吧)
}
}
return;
}
然后是匹配的代码:
int AC_ask(string a){
int p=1,ans=0,len=a.length();
for(int i=0;i<len;i++){//根据匹配串的字符进行遍历。
p=trie[p][a[i]-‘a‘];
for(int j=p;j && sum[j]!=-1;j=fail[j]){//对每一个字符进行遍历。
//注意一下循环条件,第一个是没有指向空(j),第二个是之前没有遍历过(sun[j]!=-1)
//注意之后不是 j++,而是 j=fail[j],即走到自己的 fail 指针,直到其为空。
ans+=sum[j];//统计答案。
sum[j]=-1;//将其标记为已经经过,不用进行重复遍历。
}
}
return ans;//返回答案。
}
最后是 main 函数的代码:
int n,trie[N][30],sum[N],fail[N],tot=1;
string s,a;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>s;
insert(s);//插入。
}
cin>>a;
get_fail();//找 fail[] 指针。
printf("%d\n",AC_ask(a));//输出。
return 0;
}
其实...就是多做题,没有什么窍门的好吗。
然后先是模板题,用上面的代码就可以过了。
其他的...之后补锅吧。
之前说了,我的了解只是皮毛。
想要更进一步的话,可以去看看集训队的论文。(2004 多串匹配算法及其启示——朱泽园)
网上应该是搜的到的,如果没有可以私信或者 QQ 找我要,我会不会回就看情况了。(QQ 自己去翻这篇文章)
注意,本文部分解释和我的 AC 自动机启蒙来自yyb 神犇的文章,侵权请删。
完结撒花。
原文:https://www.cnblogs.com/lpf-666/p/12638777.html