题目描述
某售货员小T要到若干城镇去推销商品,由于该地区是交通不便的山区，任意两个城镇
之间都只有唯一的可能经过其它城镇的路线。 小T 可以准确地估计出在每个城镇停留的净收
益。这些净收益可能是负数，即推销商品的利润抵不上花费。由于交通不便，小T经过每个
城镇都需要停留，在每个城镇的停留次数与在该地的净收益无关，因为很多费用不是计次收
取的，而每个城镇对小T的商品需求也是相对固定的，停留一次后就饱和了。每个城镇为了
强化治安，对外地人的最多停留次数有严格的规定。请你帮小T 设计一个收益最大的巡回方
案,即从家乡出发，在经过的每个城镇停留，最后回到家乡的旅行方案。你的程序只需输出
最大收益，以及最优方案是否唯一。方案并不包括路线的细节，方案相同的标准是选择经过
并停留的城镇是否相同。因为取消巡回也是一种方案，因此最大收益不会是负数。小T 在家
乡净收益是零，因为在家乡是本地人，家乡对小 T当然没有停留次数的限制。
Input
输入的第一行是一个正整数ｎ(5<=n<=100000)，表示城镇数目。城镇以１到ｎ的数命名。小T 的家乡命
名为１。第二行和第三行都包含以空格隔开的ｎ－１个整数，第二行的第ｉ个数表示在城镇
ｉ＋１停留的净收益。第三行的第ｉ个数表示城镇ｉ＋１规定的最大停留次数。所有的最大
停留次数都不小于２。接下来的ｎ－１行每行两个１到ｎ的正整数ｘ，ｙ，之间以一个空格
隔开，表示ｘ，ｙ之间有一条不经过其它城镇的双向道路。输入数据保证所有城镇是连通的。
Output
输出有两行，第一行包含一个自然数，表示巡回旅行的最大收益。如果该方案唯一，在
第二行输出“solution is unique”，否则在第二行输出“solution is not unique”。
Sample Input
9
-3 -4 2 4 -2 3 4 6
4 4 2 2 2 2 2 2
1 2
1 3
1 4
2 5
2 6
3 7
4 8
4 9
Sample Output
9
solution is unique
//最佳路线包括城镇 1，2， 4， 5， 9。
思路
因为题目中提到有n个点而只有n-1条边，我们就要想到树这种结构。
我们先来考虑最大收益的问题,每个点的最大收益都与它的子节点有关，一个点的最大收益就是它的每个走过的子节点的收益再加上它自己的收益。废话
因为我们最后要回到1号节点我们考虑，设n节点最多经过d次，我们先来到n节点算一次，之后每次从子树回到n算一次则一共可以走n-1个子树。
举个例子（一种颜色代表经过一次2点，若经过所有2的子树要经过2点3+1=4次）
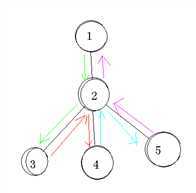由于最后要求我们收益最大。我们可以对一个节点的每个子节点进行排序，在子树收益大于零的前提下取前day[u]-1的所有子树，再向上传递，最后输出即可，但如果最后节点1的收益小于零，直接输出0即可，因为题目中也说了，在家乡不动也是一种方案。
做法：建一个大根堆的数组（或存在数组之中sort也可），将每个u节点的子节点和对应收益放入队列，每次取队首，直到去了day[u]-1次或队首节点收益小于零。
之后再来考虑多种情况问题，对于每一个节点u，使它不唯一的情况有以下几种：
1.它走过的其中一个或多个子节点情况不唯一。
2.在它取的day[u]-1个节点中有收益为零得点（取或不取的收益一样）。
3.队列中第day[u]-1的节点的收益与第day[u]个相同（去哪一个都一样）。
根据以上思路，我们就可以解决这道题目了。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<queue> 5 using namespace std; 6 const int N=1e6+10; 7 int Head[N],tot; 8 struct Node{ 9 int to,next; 10 }edge[N]; 11 void Add(int x,int y){ 12 edge[++tot].to=y; 13 edge[tot].next=Head[x]; 14 Head[x]=tot; 15 } //前向星存储树。 16 struct son{ 17 int id,val; 18 son(int x,int y){ 19 id=x;val=y; 20 } 21 bool operator < (const son& a)const{ 22 return a.val>val; 23 } //应用大根堆。 24 }; 25 priority_queue<son>q[N]; 26 int money[N],day[N],n; //money表示每个点的收益，day为每个节点最大允许停留天数。 27 bool flag[N];//表示是否多种情况。 28 void dfs(int u,int fa){ 29 if(!u) return; 30 for(int i=Head[u];i;i=edge[i].next){ 31 int v=edge[i].to; 32 if(!v) continue; 33 if(fa==v) continue; 34 dfs(v,u); 35 q[u].push(son(v,money[v]));//将u的每个子节点存到优先队列中； 36 } 37 int val=1,id; 38 int cnt=0; 39 while(u==1||cnt<day[u]-1){ 40 if(q[u].empty()) break; 41 if(q[u].top().val<0) break; //注意这句和下面这句千万能调换，在这卡了好久。 42 val=q[u].top().val,id=q[u].top().id;q[u].pop();//调换会影响下面的判断。 43 if(flag[id]||!val) flag[u]=1; 44 money[u]+=val; //将子节点的收益放入u。 45 cnt++; 46 } 47 if(!q[u].empty()&&q[u].top().val==val) flag[u]=1; //判断多解。 48 } 49 int main(){ 50 scanf("%d",&n); 51 for(int i=1;i<n;++i){ 52 scanf("%d",&money[i+1]); 53 } 54 for(int i=1;i<n;++i) 55 scanf("%d",&day[i+1]); 56 for(int i=1;i<n;++i){ 57 int x,y; 58 scanf("%d%d",&x,&y); 59 Add(x,y);Add(y,x); 60 } 61 dfs(1,0); 62 printf("%d\n",money[1]); 63 if(!money[1]||flag[1]) printf("solution is not unique\n"); //特判，money1为0有两种情况。 64 else printf("solution is unique\n"); 65 return 0; 66 }
洛谷 P6082 [JSOI2015]salesman 树形dp
原文：https://www.cnblogs.com/li-jia-hao/p/12639370.html