插值和拟合

时间：2020-04-05 23:36:16 阅读：103 评论：0 收藏：0 [点我收藏+]

一、插值和拟合的区别

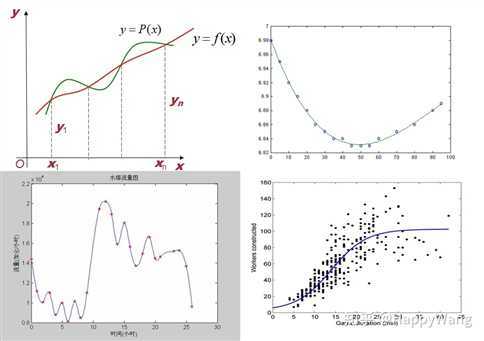
首先插值和拟合都是根据某个未知函数（或已知但难于求解的函数）的几个已知数据点求出变化规律和特征相似的近似曲线的过程。但是插值法要求的是近似的曲线需要完全经过数据点，而拟合则是得到最接近的结果，强调最小方差的概念。插值和拟合的区别如下图所示^[1]（其中左边为插值，右边为拟合）：

技术分享图片

二、常见插值法

1.基本概念

设函数 $技术分享图片$ 有n个已知数据点 $技术分享图片$ ，若存在一简单函数 $技术分享图片$ ，使 $技术分享图片$ 成立。则 $技术分享图片$ 为 $技术分享图片$ 的插值函数，点 $技术分享图片$ 为插值节点，求 $技术分享图片$ 的方法称为插值法。

作者：HappyWang
链接：https://zhuanlan.zhihu.com/p/98431641
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.拉格朗日插值

Lagrange插值多项式的公式如下：

基函数：

$技术分享图片$

插值多项式：

$技术分享图片$

插值余项：

$技术分享图片$

当 $技术分享图片$ 时，截断误差界是：

$技术分享图片$

其中： $技术分享图片$

matlab代码：

function y=Lagrange(x0,y0,x)
%输入：x0:节点变量数据
%      y0:节点函数值
%      x:插值数据
%输出：y:插值函数值
    n=length(x0);m=length(x);
    for i=1:m
        z=x(i);
        s=0.0;
        for k=1:n
            p=1.0;
            for j=1:n
                if j~=k
                    p=p*(z-x0(j))/(x0(k)-x0(j));
                end
            end
            s=p*y0(k)+s;
        end
        y(i)=s;
    end
end

例1：设 $技术分享图片$ ,并给出如下节点数据

x0=[0.4,0.5,0.7,0.8]

y0=[-0.916291,-0.693147,-0.356675,-0.223144]

估计x=0.6的值

带入Lagrange()函数，得到 $技术分享图片$ ，实际值： $技术分享图片$

3.Newton插值

上面介绍的拉格朗日插值多项式，当插值节点增减时，计算要全部进行，很不方便，所以提出一种Newton插值。

（1）差商和差分的性质

一阶差商（均差）：

$技术分享图片$

二阶差商（均差）：一阶差商的差商

$技术分享图片$

$技术分享图片$ 阶差商（均差）：

$技术分享图片$

（2）Newton插值多项式

$技术分享图片$

（3）误差

$技术分享图片$

(4)差商与导数的关系

$技术分享图片$

matlab代码如下：

function [YY,y]=newton_chazhi(X,Y,x,M)
%输入为：X-插值点的x轴向量
%Y-插值点的y轴向量
%需要求解的x变量
%M为多项式次数
%输出YY为差分表
%y是x对应的因变量
m=length(X);
YY=zeros(m);
YY(:,1)=Y;
%求查分表
for i=2:m
    for j=i:m
        YY(j,i)=(YY(j,i-1)-YY(j-1,i-1))/(X(j)-X(j-i+1));
    end
end
y=Y(1);
%计算newton插值公式
for i=1:M
    xl=1;
   for j=1:i
       xl=xl*(x-X(j));
   end
   y=y+xl*YY(i+1,i+1);
end
end


function [YY,y]=main()
X=[0.40,0.55,0.65,0.80,0.90,1.05];
Y=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];
x=0.596;
M=4;
[YY,y]=newton_chazhi(X,Y,x,M);
end

4.三次Hermite插值

$技术分享图片$

其中： $技术分享图片$ ，余项表达式：

$技术分享图片$

用Hermite进行插值时需要有确定的三个数据点以及中间点的一阶导数。

例：给定 $技术分享图片$ 求三次样条插值多项式 $技术分享图片$ ，及余项表达式。

matlab代码：

function y=hermiter_chazhi(X,Y,x1,x)
%求差分表
m=length(X);
YY=zeros(m);
YY(:,1)=Y;
for i=2:m
    for j=i:m
        YY(j,i)=(YY(j,i-1)-YY(j-1,i-1))/(X(j)-X(j-i+1));
    end
end
%求A
A=x1-YY(2,2)-(X(2)-X(1))*YY(3,3);

%求插值
y=Y(1)+YY(2,2).*(x-X(1))+YY(3,3).*(x-X(1)).*(x-X(2))+A.*(x-X(1)).*(x-X(2)).*(x-X(3));
end

function y=main_her()
x=[1/4:0.01:9/4];
f=x.^(3/2);
X=[1/4,1,9/4];
Y=[1/8,1,27/8];
x1=3/2;
y=hermiter_chazhi(X,Y,x1,x);

plot(x,y,"r")
grid on
hold on 
plot(x,f,"b")
scatter(X,Y)
legend("插值曲线","实际曲线")
end