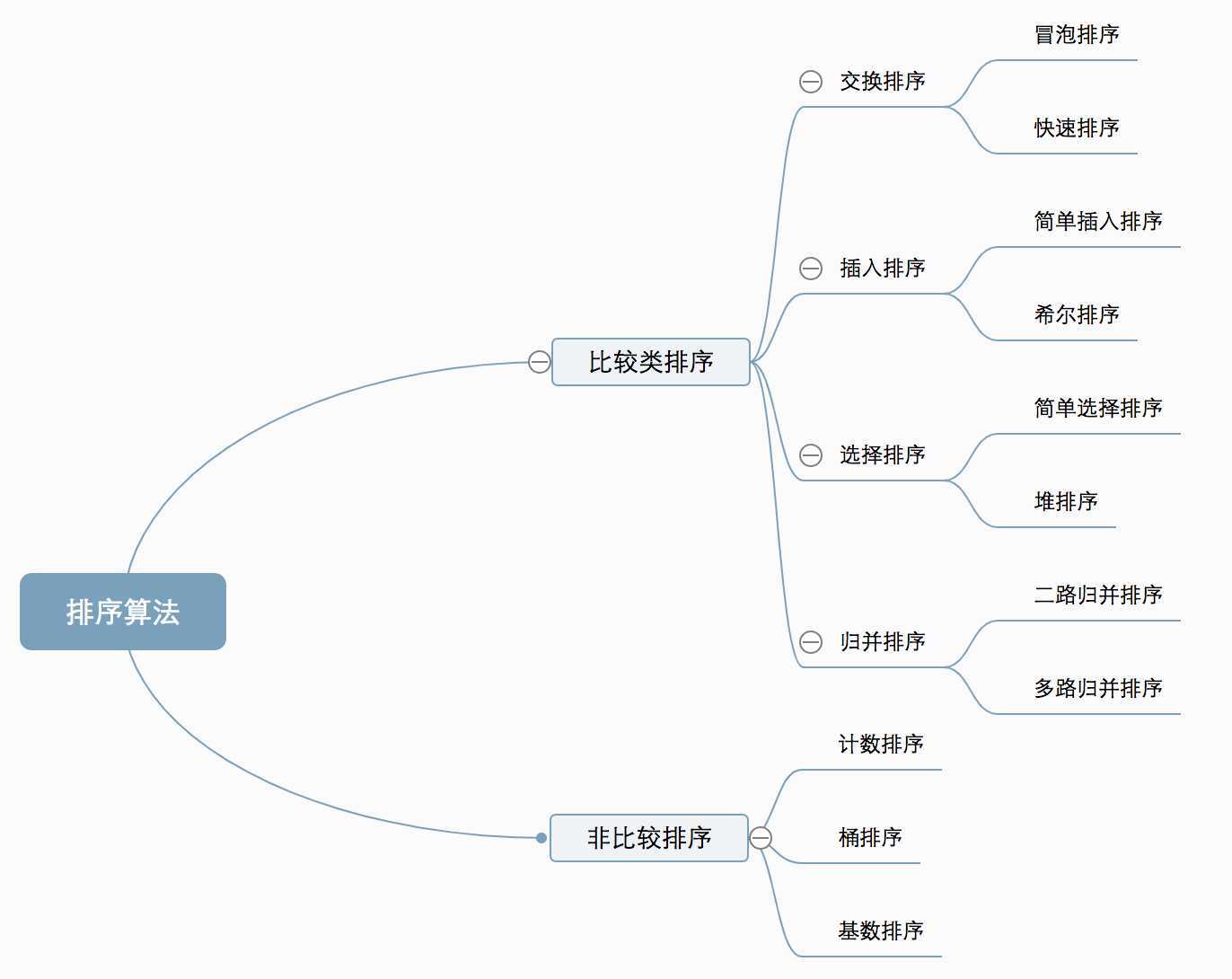
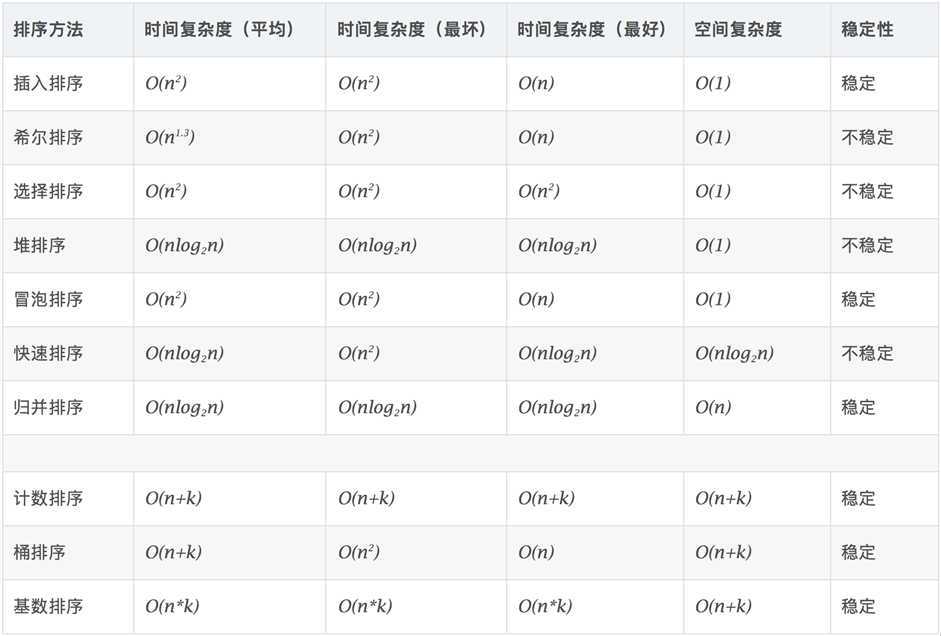
算法复杂度
1、冒泡排序
冒泡排序(Bubble sort),他重复的走访要排序的数列,一次比较两个元素,如果顺序错误,就将它们交换位置。无论是最坏时间复杂度还是平均时间复杂度都为O(n^2),但算法稳定
算法步骤:
1、比较相邻的两个元素,如果第一个比第二个大,就交换,对每一对相邻元素做同样的工作,从开始到结束,这一趟结束之后,最后那个元素就是最大的数
2、对所有的元素重复以上步骤1,除了最后一个元素
3、持续每次对越来越少的元素重复上面的操作,直到没有任何一个数字需要比较。
注意:需要控制循环的趟数以及每一趟需要比较的次数
/* 1、比较相邻的元素。如果第一个比第二个大,就交换它们两个; 2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数; 3、针对所有的元素重复以上的步骤,除了最后一个; 重复步骤1~3,直到排序完成。 */ //从小到大排序 int* BubbleSort(int MyArray[],int length) { if (!length) { return NULL; } int temp; for (int i = 0; i < length-1; i++)//表示趟数,一共是length-1次 { for (int j = 0; j < length - 1 - i; j++)//表示这一趟要比较多少次 { if (MyArray[j] > MyArray[j + 1]) { temp = MyArray[j + 1]; MyArray[j + 1] = MyArray[j]; MyArray[j] = temp; } } } return MyArray; }
2、快速排序
快速排序采用分治法策略,把一个串行(list)分成两个子串行(sub-list)。最坏的情况下,时间复杂度为O(n^2),但平均时间复杂度为O(nlogn),不稳定。
算法步骤:
1、从数列中挑出一个元素,称为基准(pivot),一般选取第一个元素作为基准
2、重新排列数列,将所有小于基准的元素放在基准的左边,大于基准的元素放在基准的右边,相同的元素可以放在任意一边,直到low不小于high。在这个分区结束后,该基准就处于数列的中间,这个称为分区(partition)操作。
3、递归把小于基准值元素的子数列和大于基准值元素的子数列排序。
int Partition(int MyArray[], int low, int high) { int pivot = MyArray[low]; while (low < high) { while (low < high && MyArray[high] >= pivot) { high--; } MyArray[low] = MyArray[high]; while (low < high && MyArray[low] <= pivot) { low++; } MyArray[high] = MyArray[low]; } MyArray[low] = pivot; return low; } int * qickSort(int MyArray[], int low, int high) { if (low < high) { int pivot = Partition(MyArray, low, high); qickSort(MyArray, low, pivot - 1); qickSort(MyArray, pivot + 1, high); } return MyArray; }
3、简单插入排序
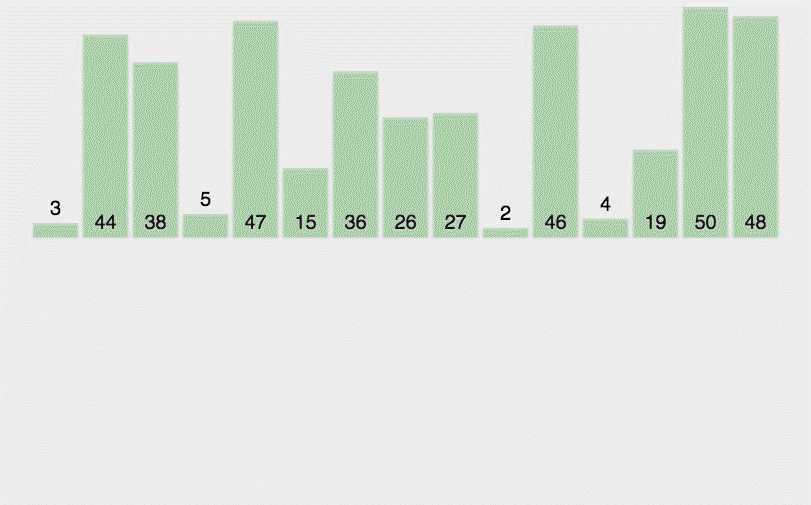
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序数列中从后向前遍历,找到相应位置插入
算法步骤:
将待排序序列的第一个元素看做一个有序序列,把第二个元素到最后一个元素当初待排序序列
从头到尾一次扫描未排序序列,将扫描到的每个元素插入到前面已排好的序列的合适的位置(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
int * insertSort(int MyArray[], int length) { for (int i = 1; i < length; i++) { int key = MyArray[i]; int j = i - 1; while (MyArray[j] > key) { MyArray[j+1] = MyArray[j]; j--; } MyArray[j+1] = key; } return MyArray; }
4、希尔排序
希尔排序,实质是分组插入排序,也称为递减增量排序算法,是插入排序的一种更高效的改进版本,但他是不稳定的排序
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1、插入排序再对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
2、但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
希尔排序的基本思想:
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
算法步骤:
选择一个增量序列t1,t2,....,tk,其中ti > tj,tk = 1;
按增量序列个数k,对序列进行k趟排序;
每趟排序根据对应的增量ti,将待排序序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
举栗子:


int* shellSort(int MyArray[], int length) { int i, j, gap; for (gap = length / 2; gap > 0; gap /= 2)//步长 { for (i = 0; i < length; i++)//直接插入排序 { for (j = i + gap; j < length; j += gap) { if (MyArray[j] < MyArray[j - gap]) { int temp = MyArray[j]; int k = j - gap; while (k >= 0 && MyArray[k] > temp) { MyArray[k + gap] = MyArray[k]; k -= gap; } MyArray[k + gap] = temp; } } } } return MyArray; }
5、简单选择排序
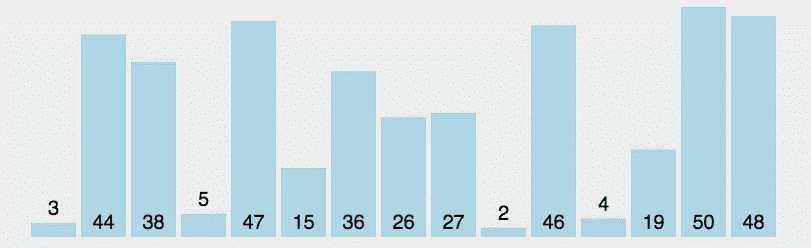
选择排序是一种简单直观的排序算法,时间复杂度都是O(n^2),所以使用这种算法数据规模越小越好。唯一的优点在于不占用额外的内存空间
算法步骤:
1、在未排序的序列中找到最小(或最大)元素,存放在排序序列的起始位置
2、再从剩下未排序元素中继续寻找最小(最大)元素,然后放到已排序序列的尾部
3、重复第二步,直到所有元素排序完毕
int * selectSort(int MyArray[], int length) { for (int i = 0; i < length; i++) { int min = i; for (int j = i + 1; j < length; j++) { if (MyArray[min] > MyArray[j]) min = j; } swap(MyArray[i], MyArray[min]); } return MyArray; }
6、堆排序
先介绍下堆的概念,堆是一个顺序存储的完全二叉树,既然是顺序存储的,用的最多的也就是数组了。
堆又细分为大根堆(root节点不小于其孩子节点)和小根堆(root节点不大于其孩子节点),可以用以下关系式来表示堆:
对于n个元素的序列{R0, R1, ... , Rn}当且仅当满足下列关系之一时,称之为堆:
(1) Ri <= R2i+1 且 Ri <= R2i+2 (小根堆)
(2) Ri >= R2i+1 且 Ri >= R2i+2 (大根堆)
其中i= 1,2,3...,n/2向下取整
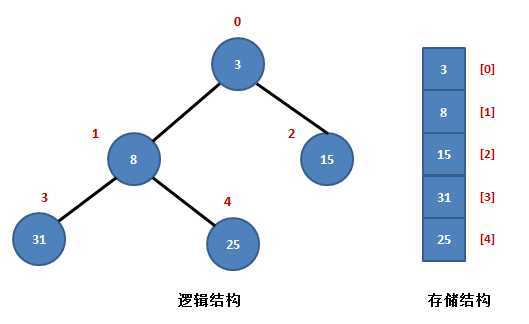
这就是一个典型的小根堆。
其父、子节点满足以下规律:
设当前元素在数组中以R[i]表示,那么,
(1) 它的左孩子结点是:R[2*i+1];
(2) 它的右孩子结点是:R[2*i+2];
(3) 它的父结点是:R[(i-1)/2];
(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2](小根堆)。
基本思路:
1、建立大堆(采用升序的方式),将n个元素组成的无序序列构建成一个大根堆
2、交换堆元素,交换堆首与堆尾元素,使堆尾称为最大元素(数组最后一元素为最大值)
3、重建大堆,将前n-1个元素组成的无序序列调整为大根堆
void adjust(int MyArray[], int len, int index) { int left = 2 * index + 1;//左节点 int right = 2 * index + 2;//右节点 int maxIndx = index; if (left<len && MyArray[left] > MyArray[maxIndx]) maxIndx = left; if (right < len && MyArray[right]>MyArray[maxIndx]) maxIndx = right; if (maxIndx != index) { swap(MyArray[maxIndx], MyArray[index]); adjust(MyArray, len, maxIndx);//递归创建最大堆 } } int * heapSort(int MyArray[], int length) { //构建大堆 for (int i = length/2-1; i>=0; i--) adjust(MyArray, length, i); //调整大堆,将root节点(最大)放置数组尾部 for (int i = length - 1; i >= 1; i--) { swap(MyArray[0], MyArray[i]); adjust(MyArray, i, 0); } return MyArray; }
7、二路归并排序
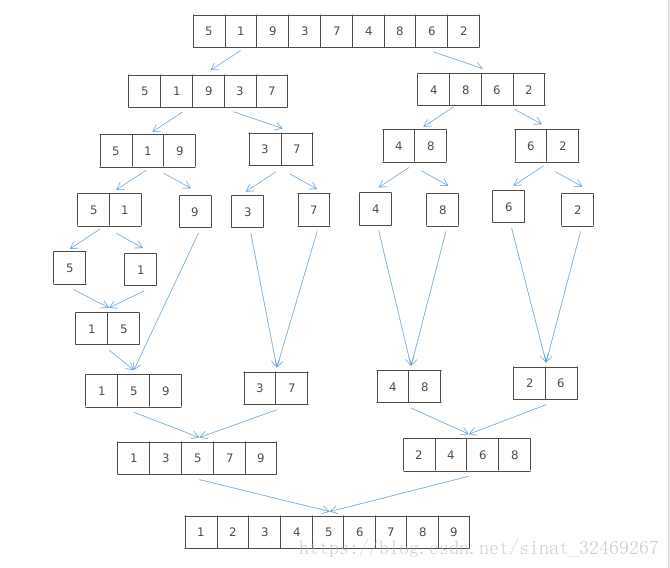
归并排序是一种稳定的排序方式,其基本思想:假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到[n/2]([x]表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,如此重复,直至得到一个长度为n的有序序列为止。
基本思路:
1、待排记录一份为二(直到待排记录只剩下一个,返回本身)
2、对前半部分归并排序
3、对后半部分归并排序
4、合并前后两部分有序序列,定义两个指针p1、p2分别指向前后两部分的起始位置,再新建一个能够容下两部分的数组,比较两个指针指向的数值大小,较小的关键字依序存入新建数组中,并将该指针后移,另一指针不变,直到所有记录存储到新建数组中。
5、新建数组中的关键字依序存储到元素组相应位置。
//将两有序数量进行合并 void mergearray(int MyArray[], int first, int mid,int last,int* temp) { int i = first, j = mid + 1; int m = mid, n = last; int k = 0; while (i <= m && j <= n) { if (MyArray[i] < MyArray[j]) { temp[k++] = MyArray[i++]; } else { temp[k++] = MyArray[j++]; } } while (i <= m) { temp[k++] = MyArray[i++]; } while (j <= n) { temp[k++] = MyArray[j++]; } for (int i = 0; i < k; i++) { MyArray[first + i] = temp[i]; } } void mergesort(int MyArray[], int first, int last,int temp[]) { if (first < last) { int mid = (first + last) / 2;//分半 mergesort(MyArray, first, mid, temp);//左边有序 mergesort(MyArray, mid + 1, last, temp);//右边有序 mergearray(MyArray, first, mid,last, temp);//合并 } } int *MergeSort(int MyArray[], int length) { int *temp = new int[length]; if (temp == nullptr) { return nullptr; } mergesort(MyArray, 0, length - 1, temp); delete[] temp; return MyArray; }
8、多路归并排序(参考:https://blog.csdn.net/u010367506/article/details/23565421)对此排序算法也并不是特别理解,先在此记录下吧
从2路到多路(k路),增大k可以减少外存信息读写时间,但k个归并段中选取最小的记录需要比较k-1次,为得到u个记录的一个有序段共需要(u-1)(k-1)次,若归并趟数为s次,那么对n个记录的文件进行外排时,内部归并过程中进行的总的比较次数为s(n-1)(k-1),若共有m个归并段,则s=logkm,所以总的比较次数为: (向上取整)(logkm)(k-1)(n-1)=(向上取整)(log2m/log2k)(k-1)(n-1),而(k-1)/log2k随k增而增因此内部归并时间随k增长而增长了,抵消了外存读写减少的时间,这样做不行,由此引出了“败者树”tree of loser的使用。在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(向上取整)(log2k)次使总比较次数为(向上取整)(log2m)(n-1),与k无关。
败者树
叶子节点记录k个段中的最小数据,然后两两进行比赛。败者树是在双亲节点中记录下刚刚进行完的这场比赛的败者,让胜者去参加更高一层的比赛。决赛,根节点记录输者,所以需要重建一个新的根节点,记录胜者(如下图节点0)。
示例:我们这里以四路归并为例,假设每个归并段已经在输入缓冲区如下图。
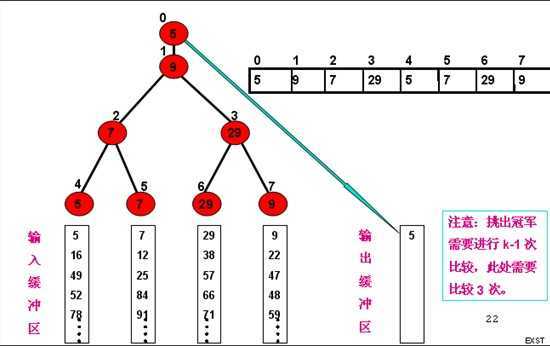
每路的第一个元素为胜利树的叶子节点,(5,7)比较出5胜出7失败成为其根节点,(29,9)比较9胜出29失败成为其根节点,胜者(5,9)进行下次的比赛9失败成为其根节点5胜出输出到输出缓冲区。由第一路归并段输出,所有将第一路归并段的第二个元素加到叶子节点如下图:
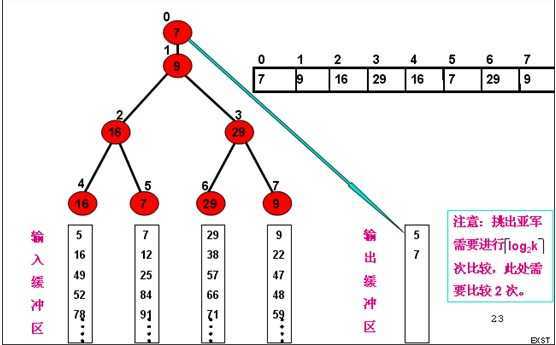
加入叶子节点16进行第二次的比较,跟胜利树一样,由于右子树叶子节点没有发生变化其右子树不用再继续比较。
#include <iostream> using namespace std; #define LEN 10 //最大归并段长 #define MINKEY -1 //默认全为正数 #define MAXKEY 100 //最大值,当一个段全部输出后的赋值 struct Array { int arr[LEN]; int num; int pos; }*A; int k,count; int *LoserTree,*External; void Adjust(int s) { int t=(s+k)/2;//ls[t]是b[s]的双亲结点的下标 int temp; while(t>0) { if(External[s] > External[LoserTree[t]]) { temp = s; s = LoserTree[t]; LoserTree[t]=temp; } t=t/2; } LoserTree[0]=s; } void CreateLoserTree() { External[k]=MINKEY; int i; for(i=0;i<k;i++)LoserTree[i]=k;//设置ls中败者的初值,简化了败者树的建立过程,这样就可以直接通过(调整过程)来建立败者树。 for(i=k-1;i>=0;i--)Adjust(i); } void K_Merge() { int i,p; //初始化External数组,用以接下来创建LoserTree for(i=0;i<k;i++) { p = A[i].pos; External[i]=A[i].arr[p]; //cout<<External[i]<<","; A[i].pos++; } //创建LoserTree CreateLoserTree(); int NO = 0; //输出最小值,并替代调整 while(NO<count) { p=LoserTree[0]; cout<<External[p]<<","; NO++; if(A[p].pos>=A[p].num)External[p]=MAXKEY; else { External[p]=A[p].arr[A[p].pos]; A[p].pos++; } Adjust(p); } cout<<endl; } int main() { //freopen("in.txt","r",stdin); int i,j; count=0; cin>>k; A=(Array *)malloc(sizeof(Array)*k); for(i=0;i<k;i++) { cin>>A[i].num; count=count+A[i].num; for(j=0;j<A[i].num;j++) { cin>>A[i].arr[j]; } A[i].pos=0; } LoserTree=(int *)malloc(sizeof(int)*k); External=(int *)malloc(sizeof(int)*(k+1)); K_Merge(); system("pause"); return 0; }
9、计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,继续排序要求输入的数据必须要确定范围的整数。
算法步骤:
1、找出待排序数组中的最大元素和最小元素
2、统计数组中为i的元素出现的次数,存入输出C的第i项
3、对所有的计数累加(从C中第一个元素开始,每一项和前一项累加)
4、反向填充目标数组:将每个元素i放在新数组的第C[i]项,没放一个元素就将C[i]减一
通俗地理解,例如有10个年龄不同的人,统计出有8个人的年龄比A小,那A的年龄就排在第9位,用这个方法可以得到其他每个人的位置,也就排好了序。当然,年龄有重复时需要特殊处理(保证稳定性),这就是为什么最后要反向填充目标数组,以及将每个数字的统计减去1的原因。
#include "CountSort.h" int * countSort(int* MyArray, int length) { int len = length; if (len <= 1) return NULL; int min = MyArray[0], max = min; for (int i = 1; i<len; ++i) { if (min>MyArray[i]) min = MyArray[i]; if (max<MyArray[i]) max = MyArray[i]; } int d = max - min ; //统计数组长度并初始化 int *countData = new int[d+1]; for (int i = 0; i <= d; i++) { countData[i] = 0; } //遍历数组,统计每个元素出现的次数 for (int i = 0; i < length; ++i) { ++countData[MyArray[i]-min]; } for (int i = 1; i <= d; i++) { countData[i] += countData[i - 1]; } int *sortedArray = new int[length]; for (int i = length - 1; i >= 0; i--) { sortedArray[countData[MyArray[i] - min] - 1] = MyArray[i]; countData[MyArray[i] - min]--; } return sortedArray; }
10、桶排序
桶排序是计数排序的升级版,利用了函数的映射关系,高效与否的关键在于这个映射函数的确定。为了使桶排序更加高效,需要做到的两点就是:
1、在额外空间充足的情况系下,尽量增大桶的数量
2、使用的映射函数能够将输入的N个数据均匀的分配到K个桶中
工作原理:
将数组分到有限数量的桶中,桶外有序,桶内无序,所以需要对每个桶再个别排序
基本思路:
1、设置一个定量的数组当做空桶子
2、寻访序列,并且把数据一个一个放到对应的桶中
3、对每个不是空的桶子进行内部排序
4、从不是空的桶子把数据在放回原来的序列中。

理论上,如果桶的数量是max-min+1,那么此时,桶排序就几乎与计数排序是一样的
#include <vector> #include <list> void insert(list<int>& bucket, int val) { auto iter = bucket.begin(); while (iter != bucket.end() && val >= *iter) ++iter; //insert会在iter之前插入数据,这样可以稳定排序 bucket.insert(iter, val); } int* bucketSort(int arr[], int length) { int len = length; if (len <= 1) return NULL; int min = arr[0], max = min; for (int i = 1; i<len; ++i) { if (min>arr[i]) min = arr[i]; if (max<arr[i]) max = arr[i]; } int k = 10;//k为数字之间的间隔 //向上取整,例如[0,9]有10个数,(9 - 0)/k + 1 = 1; int bucketsNum = (max - min) / k + 1; vector<list<int>> buckets(bucketsNum); for (int i = 0; i<len; ++i) { int value = arr[i]; //(value-min)/k就是在哪个桶里面 insert(buckets[(value - min) / k], value); } int index = 0; for (int i = 0; i<bucketsNum; ++i) { if (buckets[i].size()) { for (auto& value : buckets[i]) arr[index++] = value; } } return arr; }
参考:C++ 桶排序
11、基数排序
基数排序,简而言之就是将数字分拆为个位、十位、百位,对每个位进行排序。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能用于整数。
基数排序 vs 计数排序 vs 桶排序

#include "RadixSort.h" int maxbit(int MyArray[], int length) { int maxdata = MyArray[0]; for (int i = 1; i < length; i++) { if (maxdata < MyArray[i]) { maxdata = MyArray[i]; } } int d = 1; while (maxdata >= 10) { maxdata /= 10; d++; } return d; } int * radixSort(int MyArray[], int n) { int d = maxbit(MyArray, n); int *temp = new int[n]; int *count = new int[10];//计数器 int i, j, k; int radix = 1; for (i = 1; i <= d ; i++)//进行d次排序 { for (j = 0; j <10; j++) { count[j] = 0;//每次分配前清空计数器 } for (j = 0; j < n; j++) { k = (MyArray[j] / radix) % 10;//统计每个桶中的记录数 count[k]++; } for (j = 1; j < 10; j++) { count[j] = count[j - 1] + count[j];//将temp中的位置依次分配给每个桶 } for (j = n - 1; j >= 0; j--)//将所有桶中记录依次收集到temp中 { k = (MyArray[j] / radix) % 10; temp[count[k] - 1] = MyArray[j]; count[k]--; } for (j = 0; j < n; j++)//将临时数组的内容复制给MyArray中 { MyArray[j] = temp[j]; } radix = radix * 10; } delete[] temp; delete[] count; return MyArray; }
与桶排序代码比较可以发现,这两者存在很多的相同点。
原文:https://www.cnblogs.com/whiteBear/p/12595220.html