对简单梯度下降方法的分析总结，有关步长，梯度精度和迭代次数

我们对一组数据进行简单直线拟合时，会用到一种基础方法即梯度下降法

基本原理

• 现在我们有一组数据

• 这些数据之间的关系为

他们之间是函数关系Z(x, y)

• 现在我们要从现有的这n组数据中进行分析，最终找到一组符合这组数据的w1, w2, b，一开始我们并不清楚这三个参数
  
  

  • 首先可以初始化这三个参量都为0,并由此根据现有的x，y值算出我们对于z的预测\(A_i\)，设\(\theta\)为向量（w1， w2）

  • 之后对方差函数

    \[J(\theta) = \frac{1}{n}\sum_{i = 1}^n [z_i - (w_1 * x_i + w_2 * y_i + b)]^2 \]

    求梯度
    其梯度为

    \[\theta‘ = (\frac{\partial J}{\partial w_1}, \frac{\partial J}{\partial w_2}) \]

    有关偏导数的定义较为简洁，可自行从网上搜索

  事实上梯度所指的方向就是J函数上升最快的方向
  而我们的目标是让方差J函数尽量小，所以我们需要将\(\theta\)向梯度的反方向\(-\theta\)变化

  • 当然我们知道，这里的梯度仅仅是（w1， w2）处的梯度，w变化后梯度也会变化，所以我们需要让w变化一点点，这“一点点”我们用步长“st”表示，即
    \[\theta = \theta - \theta‘ * st \]

  st由我们自行定义

  • 对于b, 我们这样进行拟合：
    \[b = b + \frac{1}{n}\sum_{i = 1}^n [z_i - (w_1 * x_i + w_2 * y_i + b)] \]
    这样可以使b能够趋于样本中心
    
    
  • 然后重新执行前面的步骤，最终当方差小于某个值或者达到一定次数时，迭代结束，获得一组符合条件精度的w1, w2, b，完成直线拟合

• 示例代码

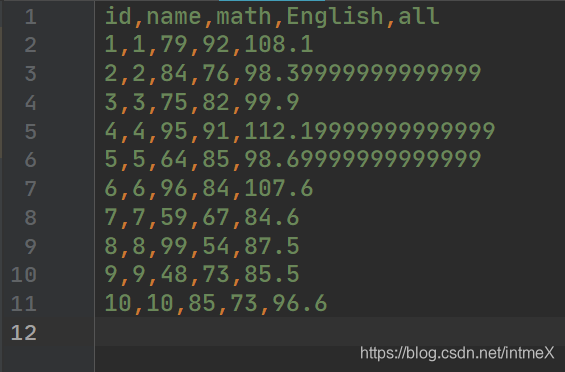
  • 其中初始参数w1，w2，b被设定为0.5，0.5，5，存放在wn.txt中

  • 十组数据存放于11.csv中，csv文件的x为“math”列，y为“English”列，z为“all”列，按照

  \[all = 0.3 * math + 0.7 * English + 20 \]

  生成(即目标w1 == 0.3，w2 == 0.7， b == 20)，如下图：
  

  • python代码如下：

import pandas as pd
import numpy as np


def initww():                   # 初始化w，b
    aa = np.zeros(3, dtype=float)
    with open("wn.txt", "r") as f:
        co = 0
        cc = f.readlines()
        for line in cc:
            aa[co] = float(line)
            co += 1
    return aa


def initcsv(csv):               # 初始化x， y
    aa = np.zeros((len(csv["math"]), 2), dtype=float)
    co = 0
    for maths in csv["math"]:
        aa[co][0] = float(maths)
        co += 1
    co = 0
    for en in csv["English"]:
        aa[co][1] = float(en)
        co += 1
    return aa


def initreals(csv):             # 初始化z
    aa = np.zeros(len(csv["all"]), dtype=float)
    co = 0
    for alls in csv["all"]:
        aa[co] = float(alls)
        co += 1
    return aa


def cost(ws, grade, truth):             # 方差函数
    pred = np.sum(grade * ws[:-1], axis=1) + ws[-1]
    return np.sum((truth - pred) ** 2) / pred.size


def gradient(ws, grade, truth, de):     # 计算梯度，传入w，b，x，y，z以及现在的方差de
    grad = np.zeros(len(ws), dtype=float)
    for i in range(len(ws) - 1):        # 计算每一分量上的偏导数
        neww = ws.copy()
        neww[i] += 0.000001
        grad[i] = (cost(neww, grade, truth) - de) / 0.000001     # 这里选取dx为0.000001，可以根据需要调整
    return grad


def gd(ws, grade, truth, de, st):       # 梯度下降，传入w，b，x，y，z以及现在的方差de, 步长st
    rate = gradient(ws, grade, truth, de)
    ws[:-1] -= rate[:-1] * st                           # 调整w
    pred = np.sum(grade * ws[:-1], axis=1) + ws[-1]
    ws[-1] += np.sum(truth - pred) / pred.size          # 调整b
    return ws


if __name__ == "__main__":
    data = pd.read_csv("11.csv")    # 读取数据并存入array数组中
    ww = initww()                   # ww[:-1]是w1，w2，ww[2]是b
    score = initcsv(data)           # 十组x，y数据
    reals = initreals(data)         # 十个z值

    d = 0.0
    for i in range(100):          # 迭代一百次
        d = cost(ww, score, reals)
        print(ww[0], " ", ww[1], " ", ww[2], " ", "cost：" + str(d))    # 每次输出w与b和方差
        ww = gd(ww, score, reals, d, 0.001)  # 梯度下降入口，步长设定为0.001

对于步长，dx和迭代次数的分析

• 上述代码解决当前问题是可以的，不过在一开始，我的步长，dx与迭代次数分别是0.01，0.01和15
• 尽管有了理论的支持，在实践中还是会遇到各种各样的错误现象，而这其中很多都表现为结果发散
  如下图
  
  可以看出发散严重

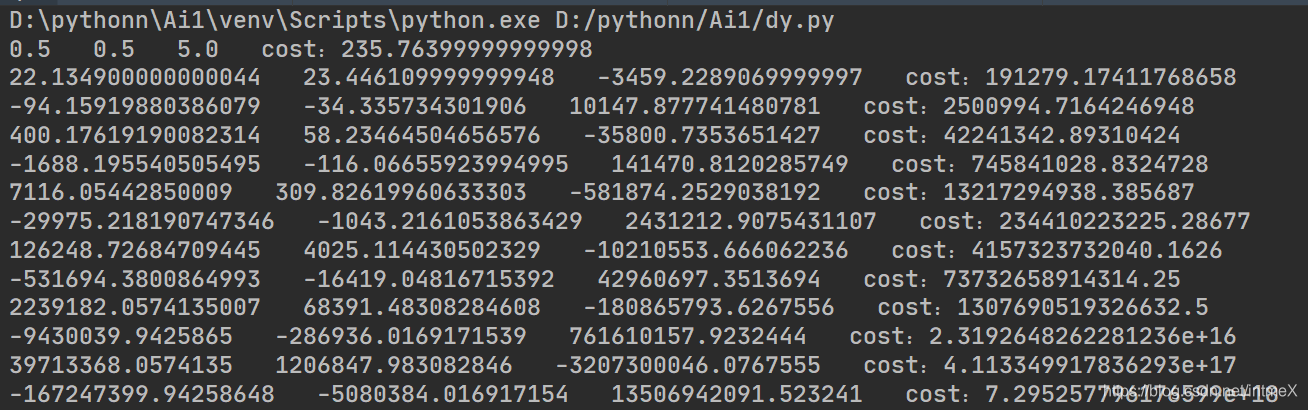
这种现象表现为发散至很大的一个数，而且发散是加速的

这种主要是步长选择不合理，每一步调整之后w的位置距离最优解差的更远了

• 我们这里w是0.1的数量级，选取0.01的步长对于它以及当前的方差函数来说，太大了，将步长改为0.001后表现如下
  

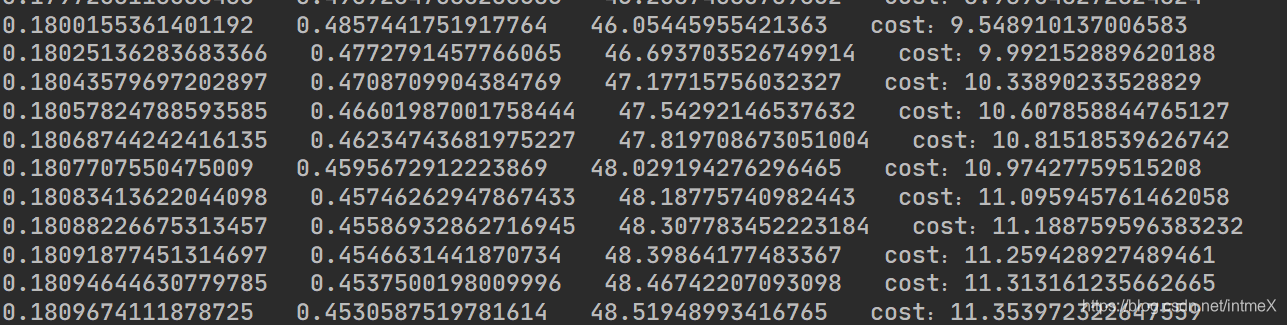
可以看到cost一开始在减小，但之后却在11.4左右趋于稳定，其他数据也是在一个数附近趋于稳定，当然我们能看到这些数据是和答案相差较多的

这种“死胡同”现象在这里是因为所求梯度不准确所致，我们知道和求导一样，dx选取越趋近于零，梯度越准确，我们这里选择的0.01可以说是“太大了”

• 将dx改为0.001后，结果如下
  

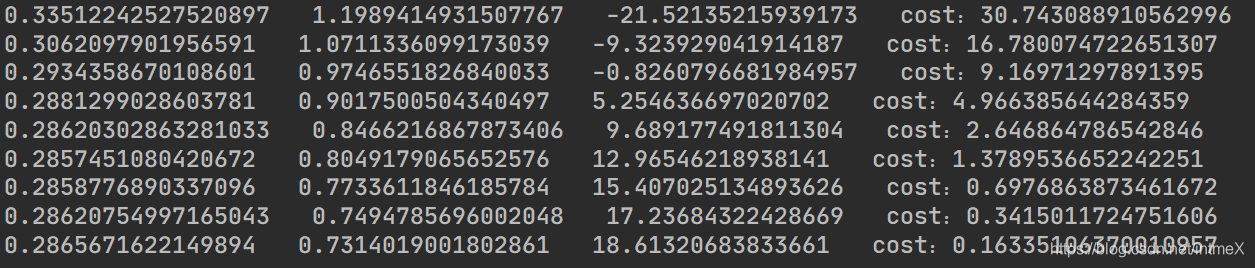
可以看出，cost降到了0.16，并且其他的参数也与答案很接近，但是这个结果对我们的要求来说可能还不够，我们需要一个更精确的结果

这里可以看出w,b的变化还可以进行下去，我们需要增加迭代次数

• 将迭代次数增加到100，结果如下
  

我们确信再往下应该不会有太多改变了，但是结果仍然有一定差距

不过以上的操作说明减小步长与dx，增加迭代次数确实可以提高预测的精度/曲线的拟合度
但是减小步长的同时我们必须增加迭代次数，由于迭代次数受限限制于当前计算机的算力，步长不可以无限减小，所以为了提高精度，我们应该主要减小dx

• 将dx改为0.000001，得到如下结果
  

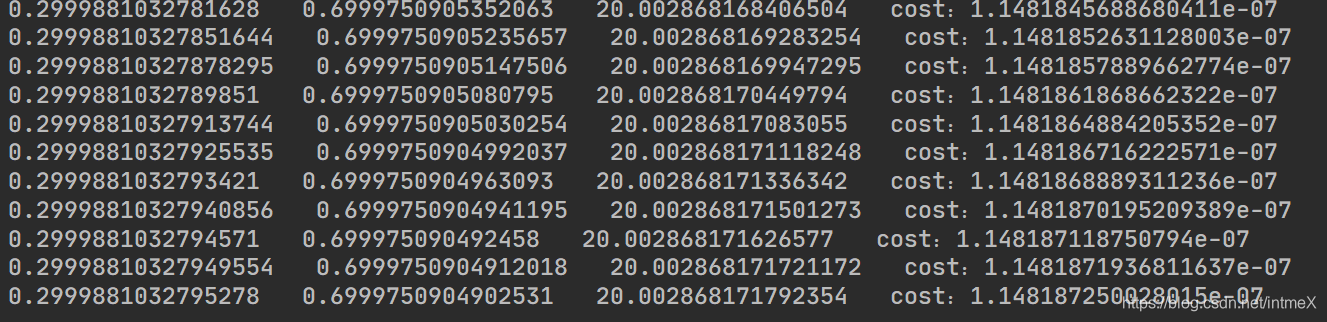
可以看出，结果可以说是基本正确了，这样我们的直线就拟合成功了

总结发现

• 1.步长选取不在于多小，而是在现有条件上选择最能满足当前问题的步长，步长减小时尽管精度增加，更不易出现发散错误，但是迭代次数要增加(当然不一定同倍数增加)
  
  

• 2.可以说迭代次数决定了我们在现有步长，dx的条件下能达到多小的误差，在迭代次数增加到一定程度后，这个误差受制于其他因素，不会再减小
  
  

• 3.而dx越小，梯度越准确，可以想到，越接近最优解（误差函数的极小值处），梯度越小，而梯度精度就越重要，所以，越小的dx决定了这个程序最终能达到多精确的拟合效果
  
  

• 补充，简单考虑时，我们可以按上面的程序里一样，直接用偏导数定义去求梯度，但是这样一定要选择一个足够小的dx才可以。我们对已知解析式的误差函数一般直接使用它的偏导函数来求梯度，这样就避免了这个问题，所以上面的程序完全可以依此改写，当然，如果误差函数不易得偏导函数，使用定义也是一种方法

对简单梯度下降方法的分析总结，有关步长，梯度精度和迭代次数

原文：https://www.cnblogs.com/int-me-X/p/12642581.html