树的遍历是一个老生常谈的话题,常见的遍历方法无非就是前序遍历、中序遍历、后序遍历以及层次遍历,如下图所示。其中前三种遍历可以基于深度优先搜索实现,而层次遍历基于广度优先搜索实现。本文主要讨论二叉树的各种遍历问题及其变体,这些方法很容易扩展到多叉树的情形,因此不再赘述。
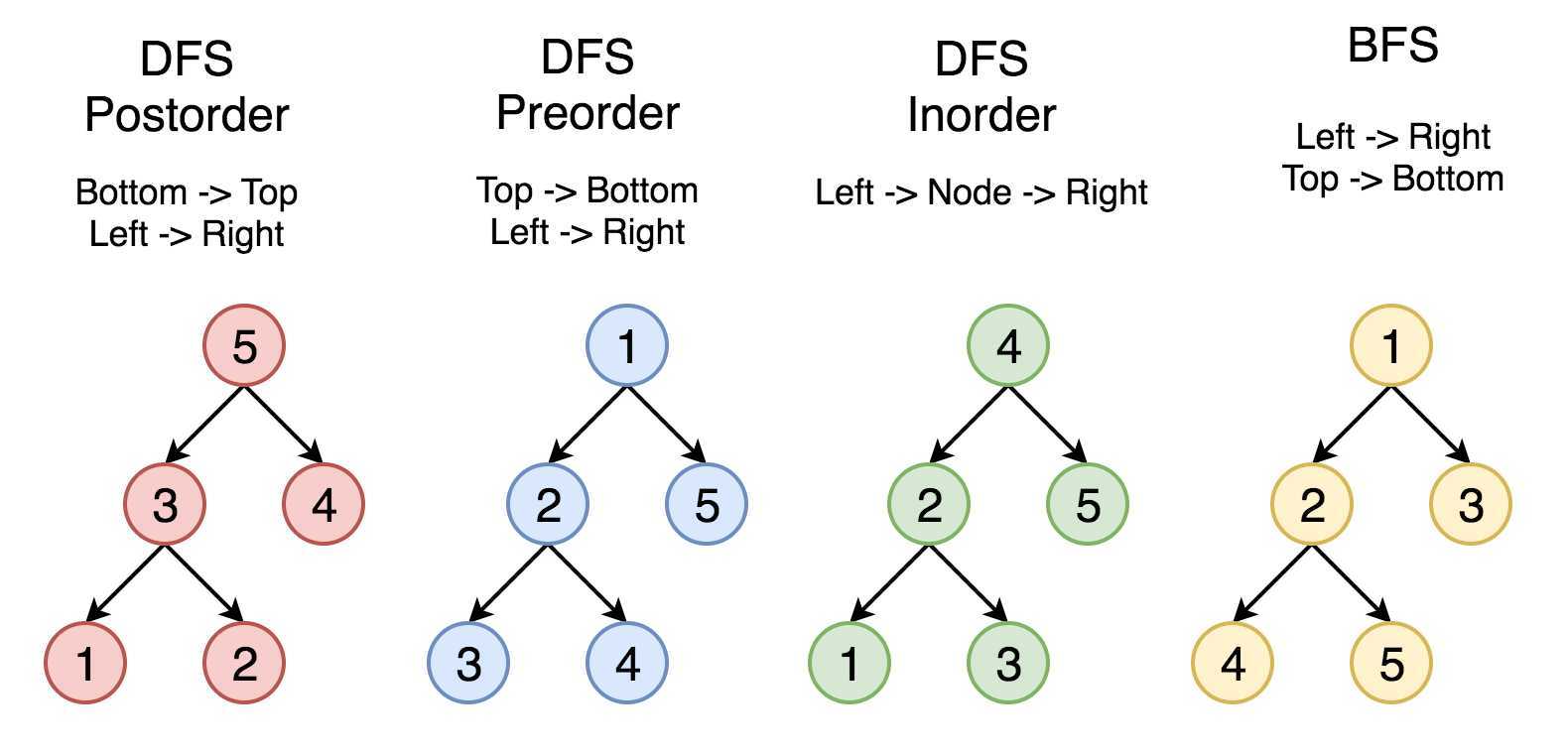
前、中、后序遍历的递归实现非常简单,我们这里就不讨论了。这一小节我们主要关注如何使用迭代的方式实现这三种遍历方式。
LeetCode 144. 二叉树的前序遍历
前序遍历按照根节点、左子树、右子树的顺序对二叉树进行访问。因此,我们可以将根节点压入栈中,然后在每次迭代中弹出当前的栈顶元素,并将其子节点压入栈中(注意要先压入右子节点再压入左子节点)最终的输出顺序就是前序遍历的顺序。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> stk;
vector<int> order;
if (root == nullptr) return order;
stk.push(root);
while (stk.size()) {
auto pval = stk.top();
stk.pop();
order.push_back(pval->val);
if (pval->right) stk.push(pval->right);
if (pval->left) stk.push(pval->left);
}
return order;
}
};
LeetCode 94. 二叉树的中序遍历
中序遍历按照左子树、根节点、右子树的顺序访问二叉树。因此,我们在访问根节点时,要保证根节点的左子树已经遍历完成。在实现上,我们先把根节点压入栈中,然后再把根节点的左子树压入栈中,每次迭代弹出栈顶元素。等到左子树和根节点全都遍历完成后,我们再把右子树压入栈中。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> stk;
vector<int> order;
auto node = root;
while (node || stk.size()) {
while (node) {
stk.push(node);
node = node->left;
}
node = stk.top();
stk.pop();
order.push_back(node->val);
node = node->right;
}
return order;
}
};
LeetCode 145. 二叉树的后序遍历
后序遍历的顺序是左子树、右子树、根节点,即先遍历左子树,再遍历右子树,最后访问根节点。在将某个节点的值加入到序列中时,我们需要确认该节点的左子树和右子树都已经完成遍历。在具体实现上,我们需要为每个节点保存一个状态信息,用来判断该节点的右子树是否已经被遍历过。如果没有遍历右子树,我们就把右子树压入栈中,否则弹出栈顶元素并将该节点的值加入到结果序列中。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
using Pair = pair<TreeNode*, bool>;
vector<int> order;
stack<Pair> stk;
auto node = root;
while (node || stk.size()) {
while (node) {
stk.emplace(node, false);
node = node->left;
}
auto& curr = stk.top();
if (curr.second) {
stk.pop();
order.push_back(curr.first->val);
} else {
node = curr.first->right;
curr.second = true;
}
}
return order;
}
};
相似题目:
LeetCode 589. N叉树的前序遍历
LeetCode 590. N叉树的后序遍历
有一类问题是根据遍历序列重构二叉树,这类问题的解题思路就是利用分治法,不断地将序列分成两部分,利用这两部分分别重构左子树和右子树。以LeetCode 105. 从前序与中序遍历序列构造二叉树为例,我们需要根据前序遍历和中序遍历序列,重新构造二叉树。我们知道,前序遍历序列中,第一个值一定是树的根节点。然后,我们在中序遍历的序列中查找根节点的位置,将中序遍历序列分成两部分,这两个子序列分别是左子树和右子树的中序遍历序列。此时,我们已经知道了左子树和右子树的中序遍历序列的长度,而一棵树的中序遍历和前序遍历的序列长度是一样的,因此,我们可以根据序列长度,在前序遍历序列中分别找到左子树和右子树的前序遍历序列。这时,我们就可以分别构建左子树和右子树了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.size() == 0 || inorder.size() == 0) return nullptr;
int root_val = *(preorder.cbegin());
auto root_it = find(inorder.begin(), inorder.end(), root_val);
if (root_it == inorder.end()) return nullptr;
int dis = distance(inorder.begin(), root_it);
vector<int> left_preorder(preorder.begin()+1, preorder.begin()+dis+1);
vector<int> right_preorder(preorder.begin()+dis+1, preorder.end());
vector<int> left_inorder(inorder.begin(), root_it);
vector<int> right_inorder(root_it+1, inorder.end());
TreeNode* root = new TreeNode(root_val);
root->left = buildTree(left_preorder, left_inorder);
root->right = buildTree(right_preorder, right_inorder);
return root;
}
};
相似题目:
LeetCode 106. 从中序与后序遍历序列构造二叉树
LeetCode 102. 二叉树的层次遍历
层次遍历就是按照每一层对树进行遍历,先遍历第一层,再遍历第二层……层次遍历实现起来非常简单,就是利用队列存储每次访问的节点以及该节点的深度。当节点出队时,将该节点的所有子节点入队,并把深度增加1,直到队列中没有元素为止。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
using Pair = pair<int, TreeNode*>;
queue<Pair> que;
vector<vector<int>> ans;
que.emplace(0,root);
while(que.size()){
auto p = que.front();
que.pop();
if(p.second){
if(ans.size() == p.first) ans.emplace_back();
ans.at(p.first).push_back(p.second->val);
que.emplace(p.first+1, p.second->left);
que.emplace(p.first+1, p.second->right);
}
}
return ans;
}
};
相似题目:
LeetCode 103. 二叉树的锯齿形层次遍历
LeetCode 107. 二叉树的层次遍历 II
LeetCode 199. 二叉树的右视图
LeetCode 429. N叉树的层次遍历
原文:https://www.cnblogs.com/littleorange/p/12638894.html