前言
留个赞吧各位。
如果有逻辑/语言不清楚或者错误的地方欢迎评论教我语文。
这段时间一直在口胡二分图的东西,感觉这个知识点好多。
挖个坑把自己埋了,看看能不能填完 ,或者说能填多少。
至于为什么很多都没有证明,因为我太菜了我证明看不懂。
发现了一个很好的证明博客地址 。
二分图是啥
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。 -------百度百科。
说的好复杂啊, 画个图理解一下。
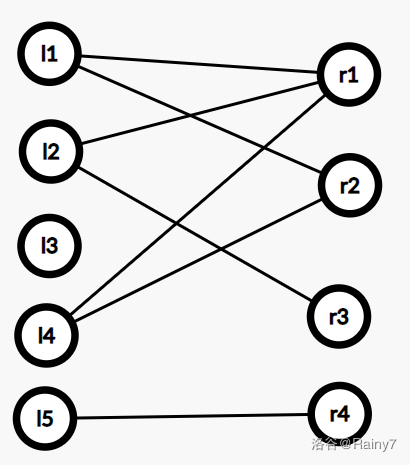
如图,在一个图中,如果能把点分为两个顶点集,使每个集合中,没有两个点有连边。
也就是说,边只会连接两个点集。
二分图判定
因为是分为两个点集,所以每个点要么属于第一个要么属于第二个。
那我们可以暴搜每个点属于什么。
显然,对于一条边所连的两个点,一定不可能属于同一个点集。
那问题可以转化一下:看成给出一个 \(n\) 个点的图,要给每个点染成黑白两色,且相邻的点颜色要不同。
那我们在搜索的时候,若点 \(u\) 属于黑色,那么与它相连的点 \(v\) 必定为白色。
这就很贪心,如果发现 \(v\) 已经被染过颜色,而且染的颜色是黑色,那么这个图就一定不是二分图了。
所以判定过程如下:
bool dfs(int x,int c)
{
color[x]=c;
for(int k=f[x];k!=0;k=p[k].nx)
{
if(color[p[k].v]==c){return 0;}
if(color[p[k].v]==0 && !dfs(p[k].v,-c)){return 0;}
}
return 1;
}
需要注意的是,给出的图不一定是连通图(除非题目有说),所以主程序的时候我们要加一个循环。
for(int i=1;i<=n;i++)
if(!color[i])
if(dfs(i,1)==0) {cout<<-1;return 0;}//不是二分图
完整代码如下:(我以前的码风有点丑哎(?))
#include<iostream>
#include<cstdio>
using namespace std;
struct node{
int v;
int nx;
}p[400001];
int f[4001],n,m,en=0;
int color[4001];
bool dfs(int x,int c)
{
color[x]=c;
for(int k=f[x];k!=0;k=p[k].nx)
{
if(color[p[k].v]==c){return 0;}
if(color[p[k].v]==0 && !dfs(p[k].v,-c)){return 0;}
}
return 1;
}
void read(int u,int v)
{
p[++en].v=v;
p[en].nx=f[u];
f[u]=en;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d %d",&u,&v);
read(u,v);
read(v,u);
}
for(int i=1;i<=n;i++)
if(!color[i])
if(dfs(i,1)==0){cout<<-1;return 0;}
printf("1\n");
for(int i=1;i<=n;i++)
if(color[i]==1)printf("1 ");
else printf("2 ");
return 0;
}
二分图匹配
二分图匹配是什么?
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
记得刚刚上面那个图嘛 (不记得就往上翻),比如这么选就是一种匹配:
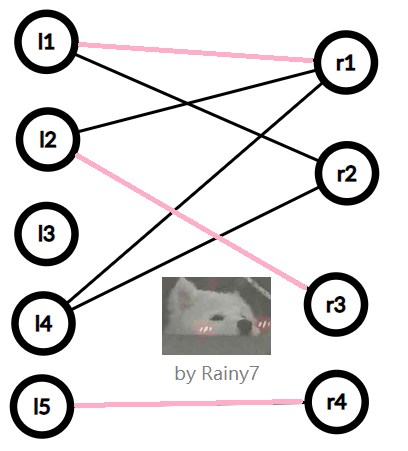
而这样就不是一个匹配:
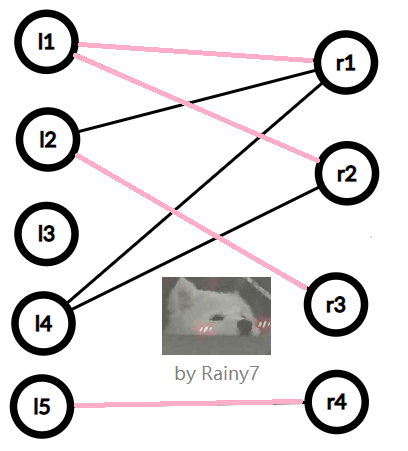
所以匹配一抓一大把。
所以要求的就成了最大匹配。
例如你谷模板 P3386 【模板】二分图最大匹配。
给定一个二分图,其左部点的个数为 \(n\) ,右部点的个数为 \(m\) ,边数为 \(e\) ,求其最大匹配的边数。
左部点从 \(1\) 至 \(n\) 编号,右部点从 \(1\) 至 \(m\) 编号。
数据范围:$1 \le n,m \le 500 , 1 \le e \le 5×10^4 , 1 \le u \le n , 1 \le v \le m $ 。
匈牙利算法
求二分图最大匹配的一般是用匈牙利算法 ,因为好写。
首先,要先知道一个叫增广路的东西。
若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径(举例来说,有A、B集合,增广路由A中一个点通向B中一个点,再由B中这个点通向A中一个点……交替进行)。 ----百度百科
好复杂啊...?那我们先不管他。
匈牙利算法就是一个不断找增广路的过程,那来手动模拟一下。
(好多人模拟过程都是男女配对啊??)
比如这个图:
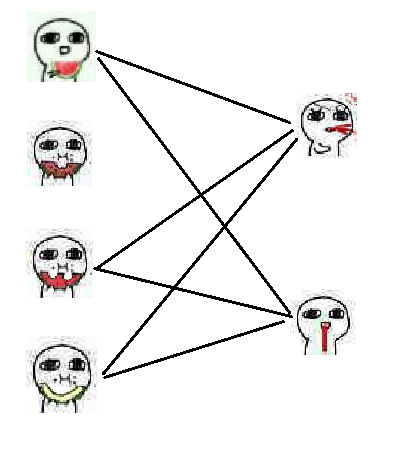
第一次匹配,我们先将第一个吃瓜人匹配到第一个吐血人:
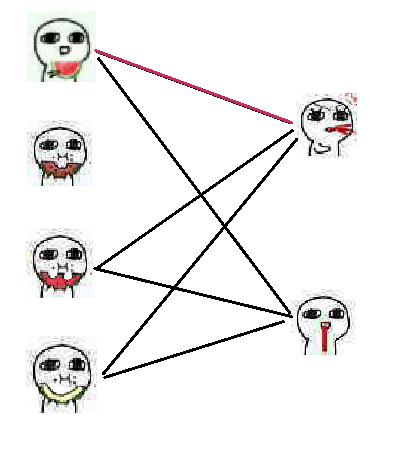
接下来,发现第二个吃瓜人是单着,那不管他了。
第三个吃瓜人,匹配到第一个吐血人,然后发现第一个吃瓜人已经和他匹配了。
那么就去协商一下,第一个吃瓜人发现还能和第二个吐血人匹配,于是第一个吐血人就给了第三个吃瓜人。如图:
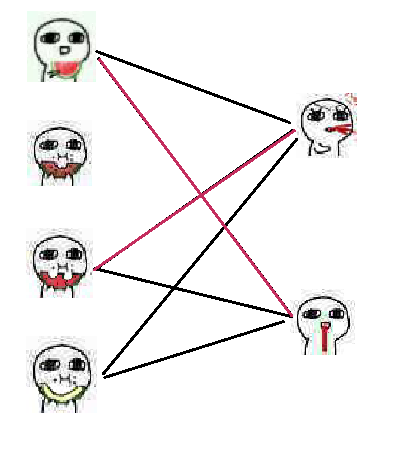
于是轮到了第四个吃瓜人,他想和第一个吐血人匹配,然后发现已经有人匹配了。
于是他和第三个吃瓜人协商, 第三个吃瓜人就选择了第二个吐血人,然后发现已经有人匹配了。
于是第三个吃瓜人去和第一个吃瓜人协商, 第一个吃瓜人选择了第一个吐血人。
结果他发现问题又绕回去了,于是第三个吃瓜人和第一个吃瓜人的协商失败,那么第三个吃瓜人和第四个吃瓜人的协商失败。
也就说,第四个人只能和第二个人一起在旁边吃瓜了。
所以最大匹配数为 \(2\) 。
这大致就是二分图匹配的过程。
而协商过程,其实就是在找增广路。
也就是每个吃瓜人,都是先选择一个未匹配的边,如果对面的点(吐血人)已经被匹配了,那就顺着那个匹配的边找到那个人,那个人再选一个未匹配的边....
复杂度为 \(O(nm)\) 。
匈牙利代码如下:
\(map_{i,j}\) 表示连边情况,\(vis[]\) 用来判断已经走过的点 , \(matched[]\) 表示改点的匹配点。
bool found(int x)
{
for(int i=1;i<=m;i++)
{
if(!map[x][i]||vis[i])continue;
vis[i]=1;
if(!matched[i]||found(matched[i]))
{
matched[i]=x;
return 1;
}
}
return 0;
}
int match()
{
int cnt=0;
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(found(i))cnt++;//找增广路
}
return cnt;
}
其他部分其实没啥亮点。
完整代码如下:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,e,matched[2001];
bool vis[2001],map[2001][2001];
bool found(int x)
{
for(int i=1;i<=m;i++)
{
if(!map[x][i]||vis[i])continue;
vis[i]=1;
if(!matched[i]||found(matched[i]))
{
matched[i]=x;
return 1;
}
}
return 0;
}
int match()
{
int cnt=0;
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(found(i))cnt++;//找增广路
}
return cnt;
}
int main()
{
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=e;i++)
{
int u,v;
scanf("%d%d",&u,&v);
map[u][v]=1;
}
printf("%d\n",match());
return 0;
}
\(\text{k}\)\(\ddot{o}\)\(\text{nig}\) 定理
这个名字真难打。
点覆盖,在图论中点覆盖的概念定义如下:对于图G=(V,E)中的一个点覆盖是一个集合S?V使得每一条边至少有一个端点在S中。 -----百度百科
举个例子:
这个图的,选择 \(2,4,5\)就是一种点覆盖。
这种情况的点覆盖数为 \(3\) 。
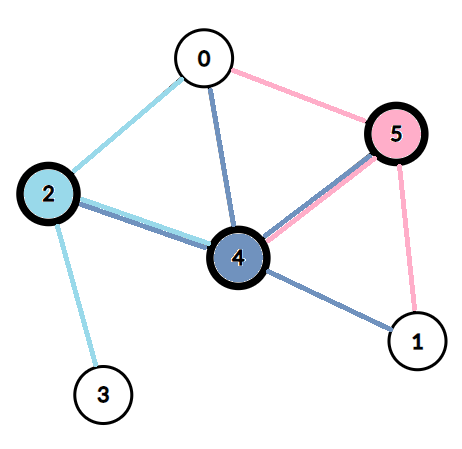
很明显,每个图的最大点覆盖就是点数。
也就是说,不存在没有点覆盖的图。
所以一般都是求最小点覆盖。
那现在来探讨一下二分图的最小点覆盖(不能遗忘标题)。
然后这就有一个定理:二分图的最小点覆盖=二分图的最大匹配
二分图的最小边覆盖。
有最小点覆盖,就有一个东西叫最小边覆盖。
边覆盖是一类覆盖,指一类边子集。具体地说,图的一个边子集,使该图上每一节点都与这个边子集中的一条边关联。 --百度百科
如图,边覆盖为 \(3\) 。
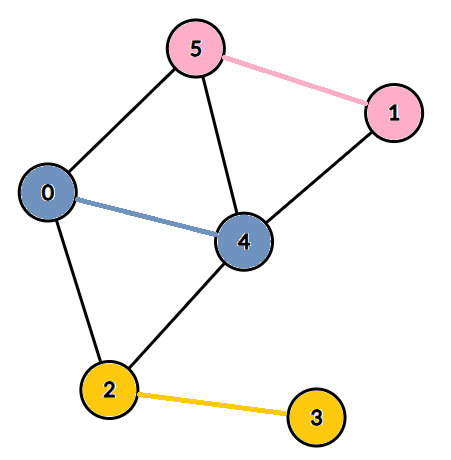
那么是否每个图都有边覆盖呢?
显然,如果一个图含有一个孤立点,那么这个图不可能有边覆盖。
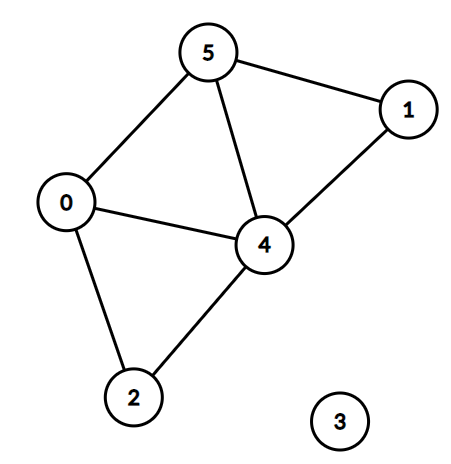
那么又有一个定理:二分图中最小边覆盖=顶点数-最小顶点覆盖。
也就是说:二分图中最小边覆盖=顶点数-二分图最大匹配
最小路径覆盖
洛谷这题正好有P2764 最小路径覆盖问题。
那么我们就用二分图过了这个网络流24题。
给定有向图 \(G=(V,E)\) 。设 \(P\) 是 \(G\) 的一个简单路(顶点不相交)的集合。如果 \(V\) 中每个定点恰好在P的一条路上,则称 \(P\) 是 \(G\) 的一个路径覆盖。 \(P\) 中路径可以从 V 的任何一个定点开始,长度也是任意的,特别地,可以为 \(0\) 。\(G\) 的最小路径覆盖是 \(G\) 所含路径条数最少的路径覆盖。设计一个有效算法求一个 GAP (有向无环图) \(G\) 的最小路径覆盖。
如下图,最小路径数为 \(3\) ,分别为:
1 4 7 10 11
2 5 8
3 6 9

结论其实又双是个定理。
考虑建一个二分图。
假设图两边的点数都为 \(n\) ,左边编号表示为 \(i\) ,右边编号表示为 \(i‘\) 。
每次读入一条边 \((u,v)\) 时,在二分图连边 \((u,v‘)\) 。
建完图跑二分图最大匹配,结果为:最小路径覆盖=顶点数-最大匹配数。
稍稍证明一下:(开始摘抄别人证明)
题目中已经说明,一个单独的点也为路径,如果 \(u_1,u_2,u_3,...u_n\) 为一条路径,那 \(u_1\) 到 \(u_n\) 之间不会有其他的有向边。
如果此时最大匹配数为 \(0\) ,则二分图中无边,显然最小路径覆盖=顶点数-最大匹配数=顶点数。
若此时增加一条匹配边 \((x,y‘)\) ,则在有向图中,\(x,y‘\)在同一条路径上,最小路径覆盖减一。
若继续增加匹配边,那么最小路径继续覆盖减一,所以公式得证。
那么路径要怎么求呢。
直接沿着增广路跑循环就可以了。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int Maxn=300+5,Maxm=6000+5;
int n,m,ans,matched[Maxn];
bool vis[Maxn],mp[Maxn][Maxn];
bool found(int x)
{
for(int i=n+1;i<=2*n;i++)
{ if(!mp[x][i]||vis[i])continue;
vis[i]=1;
if(!matched[i]||found(matched[i]))
{ matched[i]=x;
matched[x]=i;
return 1;
}
}
return 0;
}
int match()
{
int cnt=0;
for(int i=1;i<=n;i++)
{ memset(vis,0,sizeof(vis));
if(found(i))cnt++;
}
return cnt;
}
void prt(int x)
{
x+=n;
do
printf("%d ",x=x-n);
while(vis[x]=1,x=matched[x]);
printf("\n");
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
mp[u][v+n]=1;
}
ans=n-match();
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
if(!vis[i])prt(i);
printf("%d\n",ans);
return 0;
}
独立集
独立集是指图 G 中两两互不相邻的顶点构成的集合。 ---百度百科
举个例子,如下图,独立集个数为 \(3\) 。
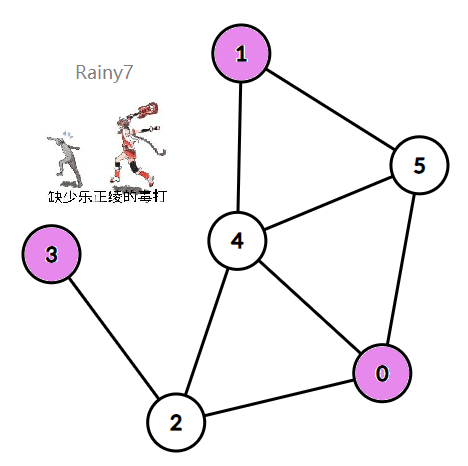
最小独立集没啥好求的,所以要解决的问题就是二分图的最大独立集。
这又双叒有一个公式:二分图的最大独立集 = 总点数-最大匹配数
KM算法
洛谷似乎没有模板,那就用这题P3967 [TJOI2014]匹配。
单看第一问就是个模板(确信)。
给定一个二分图,两边的点数都为 \(n\) ,给出若干条边,每条边有一个权值,求最大的完美匹配的值。
KM针对的是带权的完美匹配,就是说二分图两边的数量必须相等,即最大匹配数为 \(n\) 。
其实KM的复杂度和边没太多关系,所以如果两点没有连边的话,可以假设这两点的边的权值为 \(0\) 。
首先,每个点有一个顶标,就是有一个值。
假设点 \(u\) 的顶标为 \(l(u)\) 。
对于任意一条边 \((u,v)\) ,必须满足 \(l(u)+l(v) \ge w(u,v)\) ,其中\(w\)表示边权。
当一条边满足 \(l(u)+l(v)=w(u,v)\) 时,就可以把这条边加入二分图中。
如果该图可以跑出完美匹配,那么此时的完美匹配的边权值和的即为结果。
似乎很简单的样子, 那么怎么确定顶标的值呢。
因为不能直接确定,那算法流程大概是这样子:确认顶标的值->跑匹配->如果匹配数为 \(n\) ,结束;否则->修改顶标->跑匹配.....
那初始的时候顶标该如何确定呢?
假设二分图左边的顶标为 \(ex(i)\) ,右边的顶标为 \(ey(i)\) 。
因为要满足 \(ex(x)+ey(y) \ge w(x,y)\),那我们不妨直接设 \(ex(i)\) 全部为 \(0\),\(ey(i)\) 为所连边的最大值。
调整顶标过程中,其实目的就是要不断的加入新的边,也就是使更多的边满足 \(ex(i)+ey(j)=w(i,j)\) 。
那么接下来找一条边 \((i,j)\) ,使其满足 \(i\) 不在二分图最大匹配中,而 \(j\) 在二分图最大匹配中。
我们希望这边加入二分图匹配,就要使这条边满足条件,即顶标和要减少 \(d=ex(i)+ey(j)-w(i,j)\) 。
因为此时点 \(j\) 在二分图最大匹配中,如果改变顶标肯定会影响其他边,所以干脆草率一点,对于在二分图最大匹配中的任意点 \(i\) ,将 \(ex(i)+d\) 或 \(ey(i)-d\) 。
为了防止修改完导致部分顶标不满足 \(ex(x)+ey(y) \ge w(x,y)\) ,我们每次找的 \(d\) 要尽量小。
ok,解决了,算一下复杂度。
每次找边复杂度为 \(O(n^2)\) ,二分图最大匹配的复杂度为 \(O(n^2)\) ,也就是说总复杂度为 \(O(n^4)\) 。
有一说一,这是真的慢。
考虑优化,至少优化到 \(O(n^3)\) 啊!!
每次找一遍 \(d\) 太慢了,所以我们开个数组:
每次查询的时候就降了一维,\(slack\) 修改只要在跑增广路的时候修改就好了。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=303;
const int inf=1e9;
int n,map[Maxn][Maxn],matched[Maxn];
int slack[Maxn],ex[Maxn],ey[Maxn];//ex,ey顶标
bool visx[Maxn],visy[Maxn];
bool match(int x)
{
visy[x]=1;
for(int i=1;i<=n;i++)
{
if(visx[i])continue;
int gap=ex[i]+ey[x]-map[x][i];
if(gap==0)
{
visx[i]=1;
if(!matched[i]||match(matched[i]))
{
matched[i]=x;
return 1;
}
}
else slack[i]=min(slack[i],gap);
}
return 0;
}
int KM()
{
memset(matched,0,sizeof(matched));
memset(ex,0,sizeof(ex));
for(int i=1;i<=n;i++)
{
ey[i]=map[i][1];
for(int j=2;j<=n;j++)
ey[i]=max(ey[i],map[i][j]);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)slack[j]=inf;
while(1)
{
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(match(i))break;
int d=inf;
for(int j=1;j<=n;j++)
if(!visx[j])d=min(d,slack[j]);
for(int j=1;j<=n;j++)
{
if(visy[j])ey[j]-=d;
if(visx[j])ex[j]+=d;
else slack[j]-=d;
}
}
}
int res=0;
for(int i=1;i<=n;i++)
res+=map[matched[i]][i];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&map[i][j]);
printf("%d\n",KM());
return 0;
}
然后就会发现,哎不对啊这个 \(O(n^3)\) 是假的啊。
只要数据够duliu, 匹配的部分跑到 \(O(n^2)\) ,那么复杂度依然没有降到 \(O(n^3)\) 。
接下来就会发现,因为我们每次只修改一条边,也就是说dfs跑匹配的时候,有一部分和之前是一样的。
所以我们把dfs改成bfs,就可以实现真正的 \(O(n^3)\) 。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=303;
const int inf=1e9;
int n,map[Maxn][Maxn],matched[Maxn];
int slack[Maxn],pre[Maxn],ex[Maxn],ey[Maxn];//ex,ey顶标
bool visx[Maxn],visy[Maxn];
void match(int u)
{
int x,y=0,yy=0,delta;
memset(pre,0,sizeof(pre));
for(int i=1;i<=n;i++)slack[i]=inf;
matched[y]=u;
while(1)
{
x=matched[y];delta=inf;visy[y]=1;
for(int i=1;i<=n;i++)
{
if(visy[i])continue;
if(slack[i]>ex[x]+ey[i]-map[x][i])
{
slack[i]=ex[x]+ey[i]-map[x][i];
pre[i]=y;
}
if(slack[i]<delta){delta=slack[i];yy=i;}
}
for(int i=0;i<=n;i++)
{
if(visy[i])ex[matched[i]]-=delta,ey[i]+=delta;
else slack[i]-=delta;
}
y=yy;
if(matched[y]==-1)break;
}
while(y){matched[y]=matched[pre[y]];y=pre[y];}
}
int KM()
{
memset(matched,-1,sizeof(matched));
memset(ex,0,sizeof(ex));
memset(ey,0,sizeof(ey));
for(int i=1;i<=n;i++)
{
memset(visy,0,sizeof(visy));
match(i);
}
int res=0;
for(int i=1;i<=n;i++)
if(matched[i]!=-1)res+=map[matched[i]][i];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&map[i][j]);
printf("%d\n",KM());
return 0;
}
原文:https://www.cnblogs.com/Rainy7/p/12650395.html