主要还是对比一下非RNN和RNN处理序列问题的时间准确率的差别,但是因为数据的处理不同的关系下,我得出的正确率的曲线却得到了两个基本上不相同的曲线,并且在网络结构都是普通的全连接的神经网络的基础下得到的,看看第一种(低正确率的版本)
import torch import torch.nn as nn import torch.nn.functional as F import matplotlib.pylab as plt import numpy as np import os #准备数据集 path=‘C:\\Users\\Administrator\\Desktop\\code(sublime)\\python\\names‘ list_file=os.listdir(path) #建立索引 i=0 country=dict() for data in list_file: country[data[:-4]]=i i=i+1 #开始读取文件中的数据 def name_data(path): list_filename=os.listdir(path) s=[] for file in list_filename: if not os.path.isdir(file): f=open(path+"/"+file) iter_f=iter(f) for x in iter_f: s1=[] for i in x[:-1]: s1.append(ord(i)) s1.append(country[file[:-4]]) s.append(s1) #补全长度的一致性 x1=[] for t in s: x1.append(len(t)) max_len=max(x1) #开始补全长度 for a in s: if len(a)<max_len: y=max_len-len(a) for i in range(y): a.insert(-1,0) return s #print(name_data(path)) #print(len(list_file))18 #转变为tensor Batch_size=150 data=torch.Tensor(name_data(path)) #每次输入进去20个元素 train_data=DataLoader(data,batch_size=Batch_size,shuffle=True) text_data=DataLoader(data,Batch_size,shuffle=True) class Net(nn.Module): def __init__(self): super(Net,self).__init__() self.out=nn.Linear(20,50) self.out1=nn.Linear(50,18) def forward(self,x): x=F.sigmoid(self.out(x)) x=self.out1(x) return x net=Net() optizmer=torch.optim.Adam(net.parameters(),lr=0.01) loss_fun=nn.CrossEntropyLoss() def train(num): runing_loss=0 run=1 for data in train_data: x=data[:,:-1] lable=data[:,[-1]].view(1,-1) lable=lable.squeeze().type(torch.long) pre=net(x) loss=loss_fun(pre,lable) runing_loss+=loss optizmer.zero_grad() loss.backward() optizmer.step() run=run+1 print(‘第{}次的误差是{}‘.format(num,float(runing_loss/run))) def text(): total=0 right=0 for data in text_data: x=data[:,:-1] lable=data[:,[-1]].view(1,-1) lable=lable.squeeze().type(torch.long) pre=net(x) total+=lable.size(0) _,text=torch.max(pre.data,dim=1) right+=(text==lable).sum().item() l=[] for epho in range(10000): for datay in train_data: x=datay[:,:-1] #print(x[0].shape) lable=datay[:,[-1]].view(1,-1) lable=lable.squeeze().type(torch.long) pre=net(x) loss=loss_fun(pre,lable) #print(loss) optizmer.zero_grad() loss.backward() optizmer.step() #测试的环节 if epho%10==9: total=0 right=0 for datax in text_data: with torch.no_grad(): lable=datax[:,-1] total+=lable.size(0) x=datax[:,:-1] pre=net(x) _,pre1=torch.max(pre.data,dim=1) for i in range(lable.size(0)): if lable[i].data==pre1[i].data: right=right+1 print(‘正确率是{}%‘.format(right/total)) l.append(right/total) x=np.linspace(0,len(l),len(l)) y=np.array(l,np.float32) plt.plot(x,y,color=‘r‘) plt.show()
看看下面的正确率曲线:
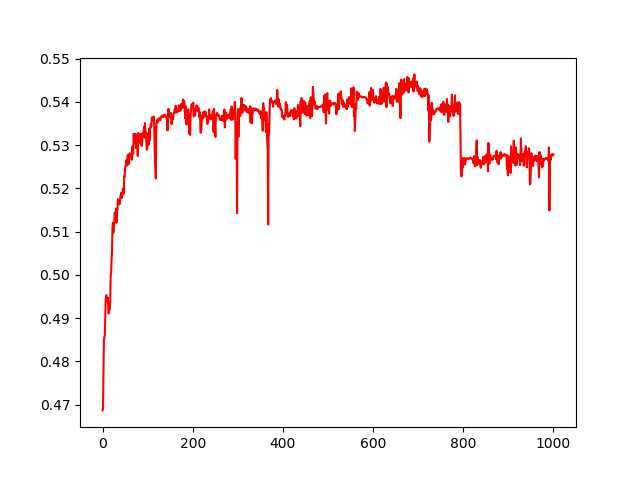
可以看出正确率及其的低下,这是因为处理数据的时候为了减少运算量但是忽略了信息量的丢失
看看下面的比较高的正确率的版本:
import glob import torch import torch.nn as nn import torch.nn.functional as F import matplotlib.pylab as plt import numpy as np import unicodedata import json import string from torch.utils.data import DataLoader import os #转换成标准的ASCII码值 all_letters = string.ascii_letters + " .,;‘" n_letters = len(all_letters) def unicode_to_ascii(s): return ‘‘.join( c for c in unicodedata.normalize(‘NFD‘, s) if unicodedata.category(c) != ‘Mn‘ and c in all_letters ) path=‘C:\\Users\\Administrator\\Desktop\\code(sublime)\\python\\names‘ list_file=os.listdir(path) #建立索引 file_name=[names[:-4] for names in list_file] #建立国家姓名的字典 def readNames(filename): if not os.path.isdir(filename): names=open(path+‘/‘+filename) return [unicode_to_ascii(name) for name in names] #构建国家-姓名之间的字典 couuntry_dic={} all_category=[] for file in file_name: name=file+‘.txt‘ names=readNames(name) couuntry_dic[file]=names #构建one-hot矩阵,字符转换成1xn_letter的tensor def code_to_tor(code): tensor=torch.zeros(1,n_letters) letter_index=all_letters.find(code) tensor[0][letter_index]=1 return tensor #姓名转换成tensor def sequence_len(file_name): l=[] for name in file_name: names=couuntry_dic[name] for i in names: l.append(len(i)) return max(l) sequence=sequence_len(file_name) def name_to_tensor(name,i): tensor=torch.zeros(1,sequence,n_letters+1) for ni,code in enumerate(name): index=all_letters.find(code) tensor[0][ni][index]=1 tensor[0][ni][n_letters]=i#每一个姓名所对应的分类 return tensor #构建数据集 def make_tensor(country): i=0 l=[] for count in country: names=couuntry_dic[count] #补全序列长度 for name in names: t=name_to_tensor(name,i) l.append(t) i=i+1 return torch.cat(l,dim=0) data=make_tensor(file_name) #[20074,19,1,58] Batch_size=150 hidden_size=18 seq_len=sequence input_size=n_letters train_loader=DataLoader(data,Batch_size,shuffle=True) text_loader=DataLoader(data,Batch_size,shuffle=True) #提取label def re_label(tes): label=tes[:,:,[-1]] l=[] label=label.numpy() for i in label: l.append(i[0][0]) return torch.Tensor(l).type(torch.long) #print(data[:,:,:,:-1].shape) class Net(nn.Module): def __init__(self): super(Net,self).__init__() self.out1=nn.Linear(1083,512) self.out2=nn.Linear(512,256) self.out3=nn.Linear(256,64) self.out4=nn.Linear(64,18) def forward(self,x): x=F.relu(self.out2(F.relu(self.out1(x)))) x=F.relu(self.out3(x)) x=self.out4(x) return x #开始训练 net=Net() optizmer=torch.optim.Adam(net.parameters(),lr=0.01) loss_fun=nn.CrossEntropyLoss() l=[] for epho in range(1000): run_time=0 loss_running=0 for data in train_loader: label=re_label(data) input=data[:,:,:-1] x=input.reshape(-1,1083)#展平 pre=net(x) loss=loss_fun(pre,label) run_time+=1 loss_running+=loss optizmer.zero_grad() loss.backward() optizmer.step() print(‘第{}次的误差是{}‘.format(epho,loss_running/run_time)) #测试的环节 if epho%10==9: total=0 right=0 for datax in text_loader: with torch.no_grad(): lable=re_label(datax) total+=lable.size(0) x=datax[:,:,:-1] x=x.reshape(-1,1083) pre=net(x) _,pre1=torch.max(pre.data,dim=1) for i in range(lable.size(0)): if lable[i].data==pre1[i].data: right=right+1 print(‘正确率是{}%‘.format(100*(right/total))) l.append(right/total) x=np.linspace(0,len(l),len(l)) y=np.array(l,np.float32) plt.plot(x,y,color=‘r‘) plt.show()
看看这个的曲线图:
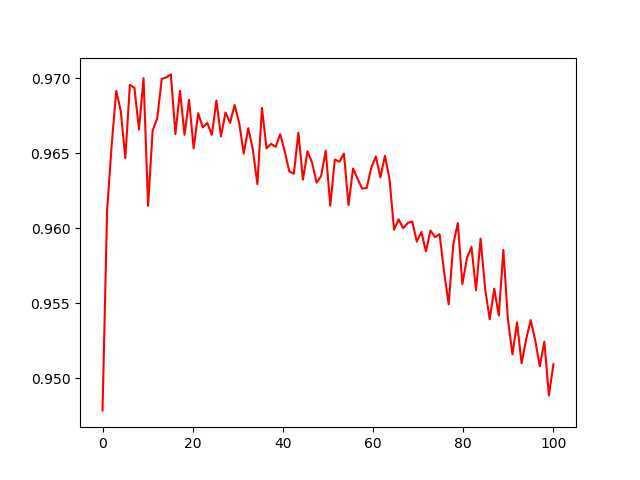
可以看出正确率的最高的时候达到了97%,但是运算时间确是极大的增加了,看看层的神经元个数就知道,这只是一些名字的复杂程度而已,要是上升到句子文章势必要更大的增加运算次数和效率的极其低下,所以这个时候RNN才会被采用。
深度学习--------------非RNN处理语言分类(one-hot)
原文:https://www.cnblogs.com/dfxdd/p/12656041.html