1 以简单线性回归为例

示例代码:
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split # 实现SimpleLinearRegressional class SimpleLinearRegressional: def __init__(self): self.a = None self.b = None def fit(self, x_train, y_train): ‘‘‘由训练集训练出模型‘‘‘ assert x_train.ndim == 1,"简单线性回归只可以处理一个特征" assert len(x_train) == len(y_train),"训练集中x的维度和y的维度必须相等" x_mean, y_mean = np.mean(x_train), np.mean(y_train) # 法二,用for循环 # num = 0.0 # d = 0.0 # for x, y in zip(x_train, y_train): # num += (x - x_mean) * (y - y_mean) # d += (x - x_mean) ** 2 # 法二:用矩阵 num = (x_train - x_mean).dot(y_train - y_mean) d = (x_train - x_mean).dot(x_train - x_mean) self.a = num/d self.b = y_mean - self.a * x_mean return self def predict(self, x_predict): return np.array([self._predict(x) for x in x_predict]) def _predict(self, x_single): ‘‘‘给定单个待预测的数据,返回预测值‘‘‘ return self.b + self.a * x_single m = 1000 big_x = np.random.random(size=m) big_y = big_x * 2 + 3.0 + np.random.normal(size=m) x_train, x_test, y_train, y_test = train_test_split(big_x, big_y, test_size=0.3, random_state=42) reg1 = SimpleLinearRegressional() reg1.fit(x_train, y_train) # 预测数据 plt.plot(big_x, reg1.predict(big_x), label = ‘fitted-curve‘) plt.show()
输出结果:
2 多元线性回归

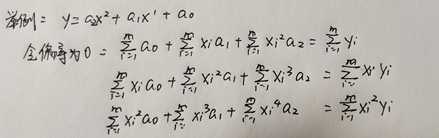

多元回归代码实现:
预测数据是: x_b.dot(theta),其中x_b表示原始x前加一列1,theta表示多元回归拟合系数
import numpy as np from sklearn import datasets from sklearn.model_selection import train_test_split class LinearRegression: def __init__(self): self.coeff_ = None self.interception_ = None self._theta = None def fit(self, x_train, y_train): ‘‘‘根据训练集训练线性回归模型‘‘‘ assert x_train.shape[0] == y_train.shape[0], "维度必须相同" # 要先加一列 x_b = np.hstack([np.ones((len(x_train), 1)), x_train]) self._theta = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y_train) self.interception_ = self._theta[0] self.coeff_ = self._theta[1:] return self def predict(self, x_predict): ‘‘‘给定预测数据集,返回表示结果‘‘‘ assert self.interception_ is not None and self.coeff_ is not None,"预测应已训练好" assert x_predict.shape[1] == len(self.coeff_), "特征维度应当相同" x_b = np.hstack([np.ones((len(x_predict), 1)), x_predict]) return x_b.dot(self._theta) boston = datasets.load_boston() x = boston.data y = boston.target x = x[y<50] y = y[y<50] x_train, x_test, y_train, y_test = train_test_split(x, y ,test_size=0.3,random_state=42) reg = LinearRegression() reg.fit(x_train,y_train) print(reg.coeff_) print(reg.interception_)
输出系数:
[-1.23818781e-01 4.03899117e-02 -4.63364280e-02 -2.99732398e-02 -1.46880633e+01 3.33324672e+00 -2.12948682e-02 -1.38818508e+00 2.31608778e-01 -1.24333203e-02 -8.57628626e-01 6.89841247e-03 -3.75313011e-01] 37.55993342611868
原文:https://www.cnblogs.com/orange-20/p/12656983.html