快速掌握算法时间复杂度与空间复杂度

时间：2020-04-08 02:03:04 阅读：73 评论：0 收藏：0 [点我收藏+]

前言

一个算法的优劣好坏，会决定一个程序运行的时间、空间。也许当小数据量的时候，这种影响并不明显，但是当有巨量数据的时候，算法的好坏带来的性能差异就会出天差地别。可以说直接影响了一个产品的高度和广度。每个程序员都想用最优的算法解决问题，我们期待自己写出的代码是简洁、高效的。但是如何评判一个算法的好坏呢？时间复杂度和空间复杂度就是一个很好的标准。

1. 时间复杂度

1.1 概念

执行算法所需要的计算工作量就是我们常说的时间复杂度。该值不一定等于接下来要介绍的基本执行次数。是一个大约的数值，具有统计意义。

1.2 基本执行次数T(n)

根据计算，得出的该算法在输入数据量为n时的，实际执行次数。该值为准确的，具体的数值，有数学意义。

1.3 时间复杂度

根据基本执行次数，去除系数、常数项等得到的渐进时间复杂度。用大O表示法。也就是说，随着数据量的剧增，不同常数项和系数，已经大致不能够影响该算法的基本执行次数。常数项和系数对于计算时间复杂度无意义

1.4 举例说明

T(n) = 2: 该函数总共执行两条语句，所以基本执行次数为2；时间复杂度为O(1): 该函数的基本执行次数只有常数项，所以时间复杂度为O(1)

void test(int n)
{
    int a;
    a = 10;
}

T(n) = 2n: 该函数共循环n次，每次执行2条语句，所以基本执行次数为2n。时间复杂度舍弃系数，为O(n)

void test(int n)
{
    int cnt;
    for (cnt = 0; cnt < n; cnt++) {
        int a;
        a= 10;
    }
}

T(n) = 2 * (1 + 2 + 3 + 4 + ... + n) + 1 = 2 * (1 + n) * n / 2 + 1 = n^2 + n + 1。因为共执行(1 + 2 + 3 + 4 + ... + n) 次循环，每次循环执行2条语句，所有循环结束后，最后又执行了1条语句，所以执行次数如上；时间复杂度为O(n^2)，因为n和常数项1忽略，它们在数据量剧增的时候，对于执行次数曲线几乎没有影响了

void test(int n)
{
    int cnt1, cnt2;
    for (cnt1 = 0; cnt1 < n; cnt1++) {
        for (cnt2 = cnt1; cnt2 < n; cnt2++) {
            int a;
            a = 10;            
        }
    }
    a = 11;
}

T(n) = 2 * logn 因为每次循环执行2条语句，共执行logn次循环；时间复杂度为O(logn)，忽略掉系数2

void test(int n)
{
    int cnt;
    for (cnt = 1; cnt < n; cnt *= 2) {
        int a;
        a = 10;
    }
}

T(n) = n * logn * 2 因为每次循环2条语句，共执行n * logn次循环；时间复杂度为O(nlogn)，忽略掉系数2

void test(int n)
{
    int cnt1, cnt2;
    for (cnt1 = 0; cnt1 < n; cnt1++) {
        for (cnt2 = 1; cnt2 < n; cnt2 *= 2) {
            int a;
            a = 10;
        }
    }
}

T(n) = 2 * n^3 因为每次循环2条语句，共执行n^3 次循环；时间复杂度为O(n^3)，忽略掉系数2

void test(int n)
{
    int cnt1, cnt2, cnt3;
    for (cnt1 = 0; cnt1 < n; cnt1++) {
        for (cnt2 = 0; cnt2 < n; cnt2++) {
            for (cnt3 = 0; cnt3 < n; cnt3++) {
                int a;
                a = 10;
            }
        }
    }
}

斐波那契数列的递归实现，每次调用该函数都会分解，然后要再调用2次该函数。所以时间复杂度为O(2^n)

int test(int n)
{
    if (n == 0 || n == 1) {
        return 1;
    }
    return (test(n-1) + test(n-2));
}

1.5 时间复杂度比较

O(1) < O(log2n) < O(n) < O(nlog2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

2. 空间复杂度

2.1 概念

一个算法所占用的存储空间主要包括：

程序本身所占用的空间
输入输出变量所占用的空间
动态分配的临时空间，通常指辅助变量

输入数据所占空间只取决于问题本身，和算法无关。我们所说的空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，即第三项。通常来说，只要算法不涉及到动态分配的空间以及递归、栈所需的空间，空间复杂度通常为0(1)。

2.2 举例说明

S(n) = O(1).空间复杂度为O(1)，因为只有a, b, c, cnt四个临时变量。且临时变量个数和输入数据规模无关。

int test(int n)
{
    int a, b, c;
    int cnt;
    for (cnt = 0; cnt < n; cnt++) {
        a += cnt;
        b += a;
        c += b;
    }
}

S(n) = O(n).空间复杂度为O(n)，因为每次递归都会创建一个新的临时变量a。且共递归n次。

int test(int n)
{
    int a = 1;
    if (n == 0) {
        return 1;
    }
    n -= a;
    return test(n);
}

3. 函数的渐进增长与渐进时间复杂度

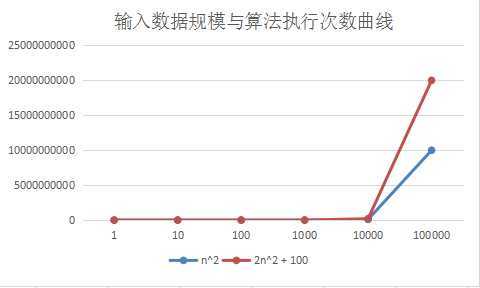
在上面的例子中，我们通常都会舍弃掉系数和常数项。这是因为当输入量剧增，接近正无穷时，系数和常数项已经不能够影响执行次数曲线。不同的系数和常数项曲线会完全重合。我做了一个折线图用来比较当输入值n激增时，n^2 曲线和 2n^2 + 100 曲线。可以看到，当数据量剧增时，系数和常数项对于统计时间复杂度都不再有意义，两条曲线几乎完全重合。

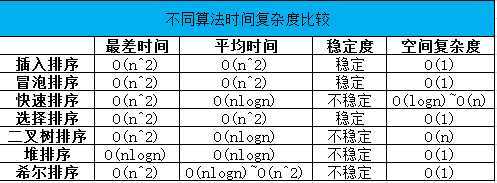
技术分享图片