树型结构是一类重要的非线性结构。树型结构是结点之间有分支,并且具有层次关系的结构,它非常类似于自然界中的树。树结构在客观世界中是大量存在的,例如家谱、行政组织机构都可用树形象地表示;树在计算机领域中也有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,可用树来组织信息;在分析算法的行为时,可用树来描述其执行过程等等。
递归是树的固有特性;
树:是n(n>=0)个结点的有限集T,满足:
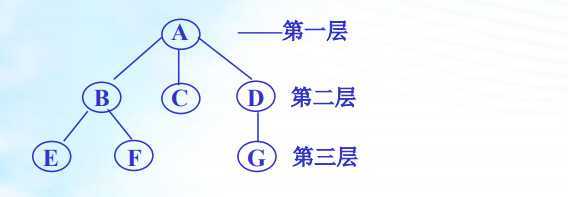
●结点:由一个数据元素及若干指向其它结点的分支所组成。
●度:结点的度:所拥有的子树的数目;树的度 :树中所有结点的度的最大值
●叶子(终端结点):度为0的结点
●非终端结点:度不为0的结点。
●孩子(子结点):结点的子树的根称为该结点的孩子。
●双亲(父结点):一个结点称为该结点所有子树根的双亲
●祖先结点:祖先指根到此结点的一条路径上的所有结点。
●子孙结点:从某结点到叶结点的分支上的所有结点称为该结点的子孙。
●兄弟结点:同一双亲的孩子之间互称兄弟。(父结点相同的结点)
●结点的层次:从根开始算起,根的层次为1,其余结点的层次为其双亲的层次加1。
●堂兄弟:其双亲在同一层的结点。
●树的深度(高度):一棵树中所有结点层次数的最大值。
●有序树:若树中各结点的子树从左到右是有次序的,不能互换,称为有序树。
●无序树:若树中各结点的子树是无次序的,可以互换,则成为无序树。
●森林:是m(≥0)棵树的集合。
对于任何一棵树:节点数=分支数+1
例如:在一颗度为3的树中,度为3的结点有4个,度为2的结点有2个,度为1的结点有3个,,则度为0的节点有几个
节点数=分支数+1=》4+2+3+n=3*4+2*2+1*3+0*n+1=》n=11
树的基本运算
二叉树在树结构的应用中起着非常重要的作用,因为二叉树有许多 良好的性质和简单的物理表示,而任何树都可以与二叉树相互转换,这 样就解决了树的存储结构及其运算中存在的复杂性
二叉树是n(n>=0)个结点的有限集合,它或为空(n=0), 或是由一个根及两棵互不相交的左子树和右子树组成,且 中左子树和右子树也均为二叉树。二叉树可以是空集合, 左子树可以为空 、右子树也可以为空。
二叉树的特点:
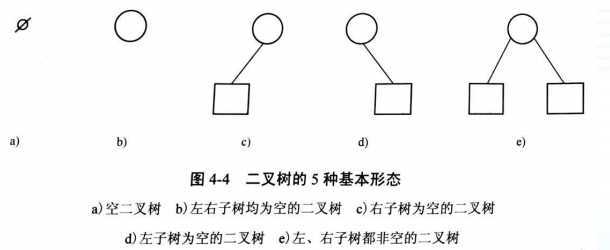
二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也 要进行区分,说明它是左子树,还是右子树。这是二叉树与树的最 主要的差别,二叉树有5种基本形态
二叉树的基本运算操作:
二叉树具有下列重要性质:
1、性质1: 在二叉树的第i(i>=1)层上至多有2^(i-1)个 结点。
2、性质2:深度为k(k>=1)的二叉树至多有(2^k) -1个 结点。
3、性质3:对任何一棵二叉树,如果其终端结点数为n0(叶子节点n0个),度为2的结点数为n2,则n0=n2+1。 即:叶结点数n0=度为2的结点数n2+1
满二叉树:深度为k(k>=1)且有(2^k) -1个结点的 二叉树;满二叉树中结点顺序编号:即从第一层结点开始自上 而下,从左到右进行连续编号。
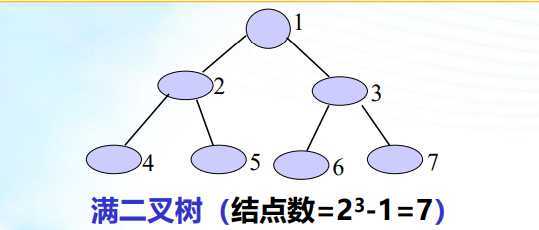
完全二叉树:深度为K的二叉树中,K-1层结点数是满的2^(k-2),K层结点是左连续的(即结点编号是连续的)
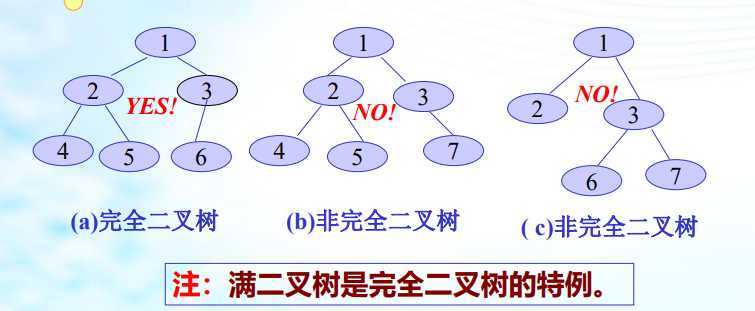
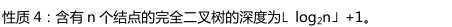
原文:https://www.cnblogs.com/jalja365/p/12601593.html