时间序列是随时间变化的序列,总体可分为 平稳 与 非平稳序列;
平稳序列即经由 样本时间序列 得到的拟合曲线在未来一段时间内仍能沿着现有形态发展下去;
数学描述如下:
均值和方差 不 随时间 t 变化而变化;
协方差 cov(xt,xt+k) 只与 周期(或者说时间间隔) K 有关,与时间 t 无关;
平稳序列又分为严平稳和弱平稳
严平稳:序列值的分布不随时间变化而变化;
如 白噪声序列,无论怎么取,均值为 0,方差为 S^2;
既然没有任何变化,就没有研究的价值了;
弱平稳:期望与相关系数(依赖性)不变,也就是说 当前序列值 与 它前些时刻的值 有关,存在依赖性;
有依赖才有研究价值;
平稳的时间序列才有研究价值;
时间序列分析针对的是 弱平稳序列;
通常情况下,非平稳序列可通过 差分变换 转化为平稳序列
DataFrame.diff(periods=1, axis=0)
periods:差分步长,xt-xt-periods;
axis:维度;
fig, axs = plt.subplots(4, 1) ##### 非平稳序列 np.random.seed(12345) ut = np.random.randint(-30, 30, size=(100)) xt = np.cumsum(ut) + 500 axs[0].plot(xt) ##### 差分变换 df = pd.DataFrame(xt) df_diff1_1 = df.diff() ### 1阶差分,步长为1 df_diff1_2 = df.diff(2) ### 1阶差分,步长为2 df_diff2 = df_diff1_1.diff() ### 2阶差分,步长为1 axs[1].plot(df_diff1_1) axs[2].plot(df_diff1_2) axs[3].plot(df_diff2) plt.show()
输出:非平稳序列、一阶差分/步长1、1阶差分/步长2、2阶差分/步长1
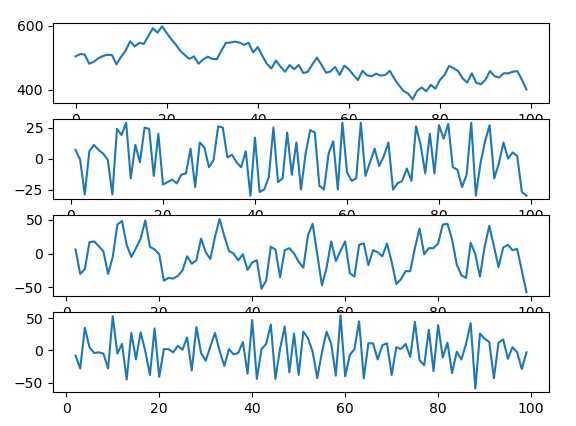
可以看到 原始数据 非平稳,后面的基本上是平稳序列;
通过差分变换 可以使得 序列平稳,但是该采用什么样的差分变换,变换后是否平稳呢?
我们可以通过 ADF 单位根检验方法 来检测序列的平稳性;
事实上,在处理时间序列时,我们首先要检测 序列的平稳性,大致流程如下
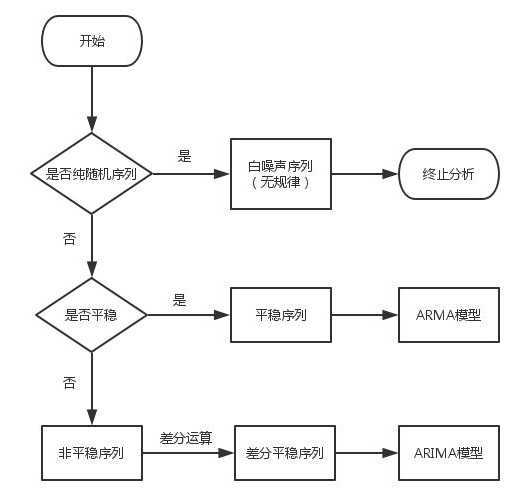
ADF检验总结一句话:如果序列是平稳的,则不存在单位根, 否则就会存在单位根
def adfuller(x, maxlag=None, regression="c", autolag=‘AIC‘, store=False, regresults=False): """ Parameters ---------- x : array_like, 1d The data series to test. maxlag : int Maximum lag which is included in test, default 12*(nobs/100)^{1/4}. regression : {‘c‘,‘ct‘,‘ctt‘,‘nc‘} Constant and trend order to include in regression. * ‘c‘ : constant only (default). * ‘ct‘ : constant and trend. * ‘ctt‘ : constant, and linear and quadratic trend. * ‘nc‘ : no constant, no trend. Returns ------- adf : float The test statistic. pvalue : float MacKinnon‘s approximate p-value based on MacKinnon (1994, 2010). """
returns:adf 是检测结果,pvalue 是 p 值
还用 差分变换 那节的例子,来解释下 ADF 检测的用法
np.random.seed(12345) ut = np.random.randint(-30, 30, size=(100)) xt = np.cumsum(ut) print(ts.adfuller(xt)) # (-1.5243530203505073, 0.5214317018385488, 0, 99, {‘1%‘: -3.498198082189098, ‘5%‘: -2.891208211860468, ‘10%‘: -2.5825959973472097}, 845.9136155157069) ##### 差分变换 df = pd.DataFrame(xt) df_diff1_1 = df.diff() ### 1阶差分,步长为1 print(ts.adfuller(df_diff1_1[1:])) # (-3.849731498648273, 0.0024375726243445746, 12, 86, {‘1%‘: -3.5087828609430614, ‘5%‘: -2.895783561573195, ‘10%‘: -2.5850381719848565}, 740.2735055354956) df_diff1_2 = df.diff(2) ### 1阶差分,步长为2 print(ts.adfuller(df_diff1_2[2:])) # (-4.012534867488554, 0.001346278712964153, 11, 86, {‘1%‘: -3.5087828609430614, ‘5%‘: -2.895783561573195, ‘10%‘: -2.5850381719848565}, 736.1426417807885) df_diff2 = df_diff1_1.diff() ### 2阶差分,步长为1 print(ts.adfuller(df_diff2[2:])) # (-5.307353752105175, 5.286830381426628e-06, 10, 87, {‘1%‘: -3.5078527246648834, ‘5%‘: -2.895382030636155, ‘10%‘: -2.584823877658872}, 744.9060722567168)
输出 第 1 个值我们称为 test result,第 2 个值我们称为 p-value;
ADF 检验的假设是 存在单位根,有两种方式检验 假设 是否成立:
1. 如果 test result 显著小于 3 个置信度(1%、5%、10%) 的临界统计值,说明是 拒绝 原假设的;
2. 如果 p-value 小于 0.05,说明是 拒绝 原假设的;
实例解读
原始数据(非平稳) 检测结果为 -1.5,大于三个临界值 -3.4,-2.8,-2.5,说明 原假设成立,存在单位根,证明为 非平稳序列;
p-value 为 0.5,远大于 0.05,原假设成立,存在单位根,证明为 非平稳序列;
这个逻辑挺绕的,总结一下,要想 序列平稳,test result 和 p-value 都要小;
参考资料:
https://www.zhihu.com/question/29128649 什么是时间序列模型,什么是弱平稳和严格平稳?
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.diff.html 差分
https://www.lizenghai.com/archives/595.html 基于Python的ADF单位根检验方法——时间序列平稳检验
https://www.zhihu.com/question/25946431 如何将非平稳的时间序列变为平稳的时间序列?
https://blog.csdn.net/qtlyx/article/details/53456480 时间序列分析这件小事(六)--非平稳时间序列与差分
https://blog.csdn.net/dingming001/article/details/73732102 差分变换进阶【有空再看看】
原文:https://www.cnblogs.com/yanshw/p/12617708.html