地址:http://codeforces.com/contest/1333

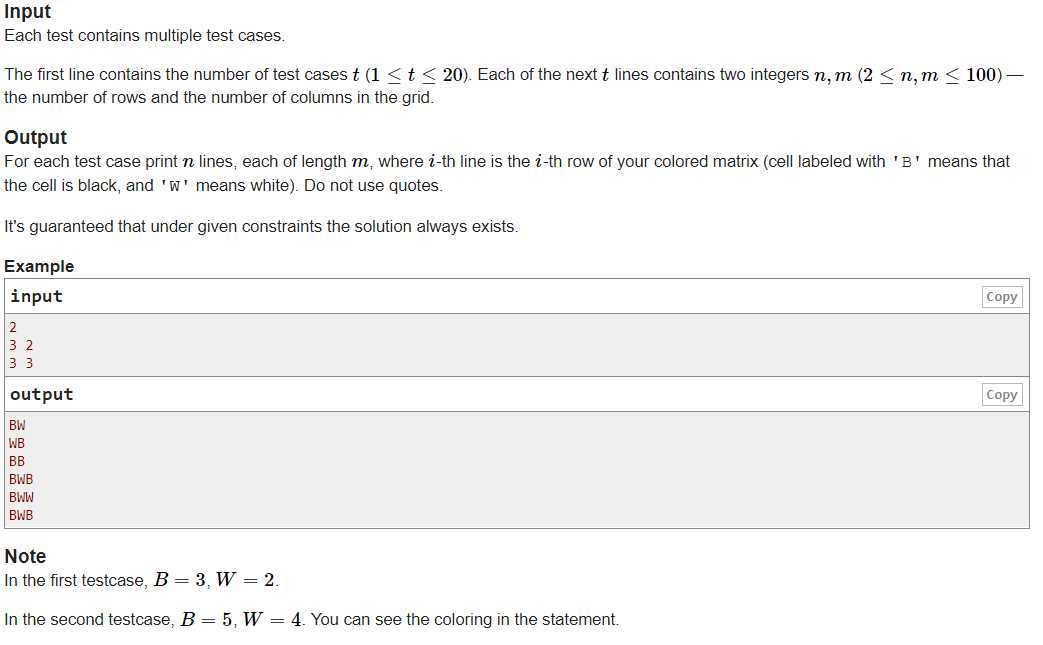
题意:满足条件:某块四周至少一个与它不同颜色。要求满足此条件的块数B=W+1。输出任意答案。
解析:想多了自己。其实只要把左上角染成W,其他全B就行了,W=1,B=2,满足条件。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<set> using namespace std; const int maxn=120; char ch[maxn][maxn]; int main() { int t; cin>>t; while(t--) { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(i==1&&j==1) cout<<"W"; else cout<<"B"; } cout<<endl; } } }

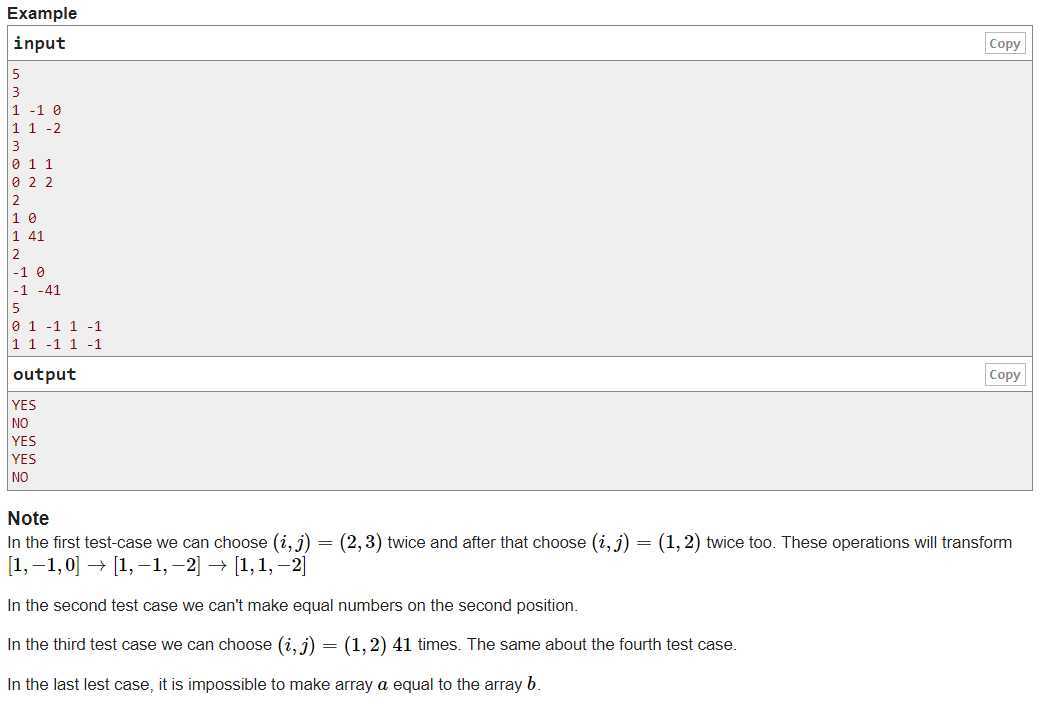
题意:给出a数组和b数组,a数组只含0,-1,1三种。操作是i<j,a[j]+=a[i]任意次。问是否可以把a数组变成b数组。
解析:不可暴力for。所以我使用vis[i]=1表示i之前有过1出现,vis[i]=2表示i之前有过-1出现。vis[i]=3表示之前1,-1均出现过。那么对于b数组里>0,看vis[]是否为2或3。<0的看vis[]是否为1,3。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<set> using namespace std; typedef long long ll; const int maxn=1e5+10; ll a[maxn],b[maxn]; int vis[maxn]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; int k1=0,k2=0; for(int i=0;i<n;i++) { cin>>a[i]; if(a[i]==-1) k2=2; if(a[i]==1) k1=1; vis[i+1]=k1+k2; } int cnt=0; for(int i=0;i<n;i++) cin>>b[i]; if(a[0]==b[0]) cnt++; for(int i=1;i<n;i++) { if(a[i]==b[i]) { cnt++; } else if(a[i]>b[i]) { if(vis[i]==3||vis[i]==2) cnt++; } else { if(vis[i]==3||vis[i]==1) cnt++; } } if(cnt==n) cout<<"YES"<<endl; else cout<<"NO"<<endl; } }

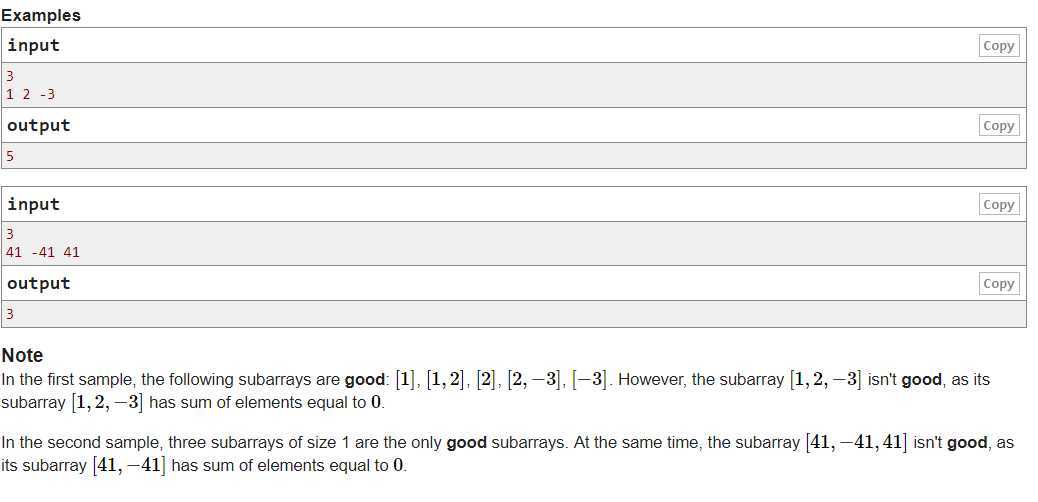
题意:一个子串里没有sum=0的即为good子串,求good子串数。1,2,3所包含的子串有:1,2,3,|1,2|,|1,2,3|,|2,3|。注意|1,3|不算!所以根据此可以推出,以i为右端点的子串有i-起始点+1个。
解析:应用前缀和a[],假如a[L]==a[R],说明L+1到R这一段的和为0,不能包含在各种good子串内。假设[L,R]区间和为0,L为以R为右端点区间和为0的最近左端点。设maxx=L+1。那么[L+1,R]这一段,整个有R-L个子串,除去sum==0的整个[L+1,R],还剩[R-L-1]个为good子串即:[R-maxx]个。用map来记录各个前缀和的最后出现位置。自然也就记录到了L的最后出现位置。
#include<iostream> #include<cstring> #include<map> using namespace std; typedef long long ll; const int maxn = 2e5+10; ll a[maxn]; int main() { map<ll,ll>m; int n; cin>>n; a[0]=0; m[0]=0; for(int i=1;i<=n;i++) { ll x; cin>>x; a[i]=a[i-1]+x; } ll sum=0; ll maxx=0; for(int i=1;i<=n;i++) { if(m.count(a[i])) //a[i]之前出现过,下行就找到它的最后出现位置 maxx=max(maxx,m[a[i]]+1); sum+=i-maxx; m[a[i]]=i; // cout<<sum<<endl; } cout<<sum<<endl; }
Codeforces Round #632 (Div. 2)
原文:https://www.cnblogs.com/liyexin/p/12675486.html