图的存储

以这幅图作为例子，我们来讲讲如何存储一幅图

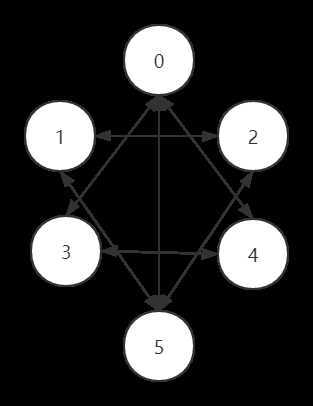
　　第一种办法是使用邻接矩阵。其实质是使用一个二维数组进行图的存储。对于样例，我们可以这样存储：

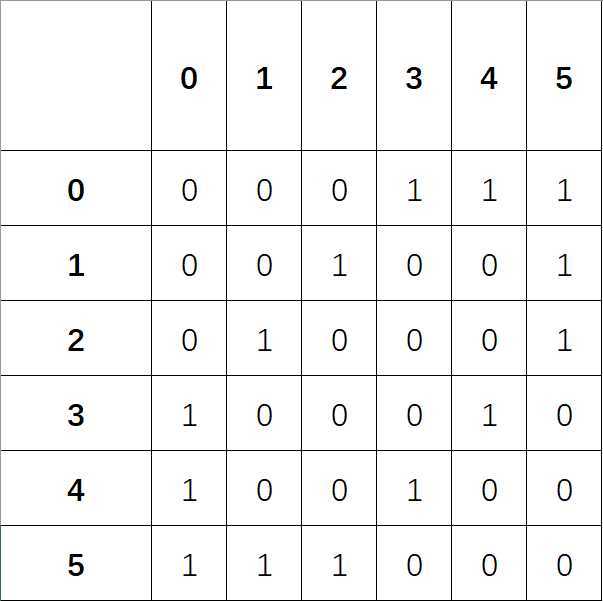
　　这样的存储方式很容易理解，例如：（2,1）这个点的值为一，说明顶点2与顶点1之间存在一条边；（4,2）这个点的值为0，说明顶点4与顶点2之间不存在边。对于有权图，我们可以把1改为边的权值。 

　　第二种办法是前向星。首先我们需要给边排序，以怎么的规则排序的。以边的起点作为关键字排序。对于例子中的这个图，我们可以这样排序：

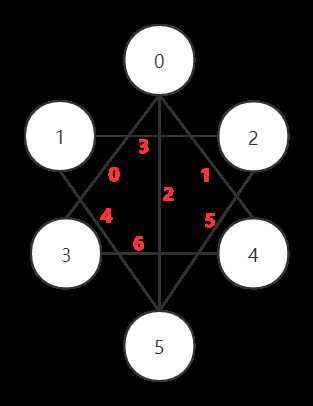
　　注意：这里边上的数值并不是边权，只是标号

　　然后我们将这些边按编号存入edge数组中（实际上是将该边连接的另一个顶点存储在数值中），并且对于每个顶点i编号最小的那条边，我们将它的编号存在head[i]中；编号最大的那条边，我们将其存在tail[i]中。 这样，我们就知道与顶点i相连的边是edge数组中从下标为head[i]到tail[i]的边。此外，可以用一个存储每个顶点的度的数组来替代tail数组。

　　还有一种方法是链式前向星。

 1 int head[maxNodeSize] = {0};    //记录各个顶点的第一条边
 2 
 3 //用于存储边的结构
 4 struct node {
 5     int to;     //边的终点
 6     int next;   //与该边同起点边的下一条边
 7 };
 8 struct node edge[maxEdgeSize] = {0};
 9 int num = 0;    //目前边的总数
10 
11 void add(int from, int to) {
12     ++num;
13     edege[num].to = to;
14     edge[num].next = head[from];    //原起点边变成新边的下一条边
15     head[from] = num;               //使新边成为该顶点的起点边
16 }

　　当然，存储图的方式有很多种，本篇博客只是讲述了其中的三种，有兴趣的朋友可以自行搜索学习。

图的存储

原文：https://www.cnblogs.com/zymmyz/p/12579672.html