1 思想
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
2 算法描述
3 举例
假设10个数为:64、8、216、512、27、729、0、1、343、125,为方便起见我们将不足三位的数以高位补零的方式全部补为三位数。
高位补零后这10个数为:064、008、216、512、027、729、000、001、343、125.
第一趟桶式排序(个位):
| 000 | 001 | 512 | 343 | 064 | 125 | 216 | 027 | 008 | 729 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
存入到桶中以后按照桶的顺序 依次取出 存入到原来的数组中
第二趟桶式排序(十位):

存入到桶中以后按照桶的顺序 依次取出 存入到原来的数组中
第三趟桶式排序(百位):
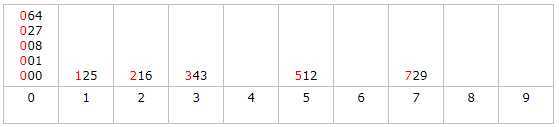
存入到桶中以后按照桶的顺序 依次取出 存入到原来的数组中,此时发现数组已经是有序的了
4 基数排序(桶排序)代码推导
1 public static void main(String[] args) { 2 int[] arr = { 58, 3, 542, 748, 14, 214 }; 3 radixSort(arr); 4 } 5 // 基数排序方法 6 public static void radixSort(int[] arr) { 7 // 第1轮 (针对每个元素的个位进行排序处理) 8 9 // 定义一个二维数组,表示10个桶,每个桶都是一个一维数组 10 // 1 二维数组包含10个一维数组 11 // 2为了防止在放入数的时候,数据溢出,则每一个一维数组 大小定义为arr.length 12 // 3很明确 基数排序用空间换时间的经典算法 13 int[][] bucket = new int[10][arr.length]; 14 15 // 为了记录每个桶中 实际存放了多少个数据 我们定义一个一维数组 来记录 16 // 各个桶的每次放入的数据个数 17 int[] bucketElementCounts = new int[10]; 18 19 for (int j = 0; j < arr.length; j++) { 20 // 取出每个元素的个位的值 21 int digitOfElement = arr[j] / 1 % 10; 22 bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j]; 23 bucketElementCounts[digitOfElement]++; 24 } 25 26 // 按照这个桶的顺序(一位数组的下标 取出数据,放入原理的数据) 27 int index = 0; 28 for (int k = 0; k < bucketElementCounts.length; k++) { 29 // 如果桶中有数据 才放入到原数组 30 if (bucketElementCounts[k] != 0) { 31 // 循环该桶 即第K个桶 放入 32 for (int l = 0; l < bucketElementCounts[k]; l++) { 33 arr[index] = bucket[k][l]; 34 index++; 35 } 36 } 37 // 第1轮处理后,需要将每个bucketElementCounts[k] = 0 清零 38 bucketElementCounts[k] = 0; 39 } 40 // [542, 3, 14, 214, 58, 748] 41 System.out.println("第一轮结果" + Arrays.toString(arr)); 42 43 // 第2轮 (针对每个元素的个位进行排序处理) 44 for (int j = 0; j < arr.length; j++) { 45 // 取出每个元素的十位的值 46 int digitOfElement = arr[j] / 10 % 10; 47 bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j]; 48 bucketElementCounts[digitOfElement]++; 49 } 50 51 // 按照这个桶的顺序(一位数组的下标 取出数据,放入原理的数据) 52 index = 0; 53 for (int k = 0; k < bucketElementCounts.length; k++) { 54 // 如果桶中有数据 才放入到原数组 55 if (bucketElementCounts[k] != 0) { 56 // 循环该桶 即第K个桶 放入 57 for (int l = 0; l < bucketElementCounts[k]; l++) { 58 arr[index] = bucket[k][l]; 59 index++; 60 } 61 } 62 bucketElementCounts[k] = 0; 63 } 64 // [3, 14, 214, 542, 748, 58] 65 System.out.println("第二轮结果" + Arrays.toString(arr)); 66 67 // 第3轮 (针对每个元素的个位进行排序处理) 68 for (int j = 0; j < arr.length; j++) { 69 // 取出每个元素的百位的值 70 int digitOfElement = arr[j] / 100 % 10; 71 bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j]; 72 bucketElementCounts[digitOfElement]++; 73 } 74 75 // 按照这个桶的顺序(一位数组的下标 取出数据,放入原理的数据) 76 index = 0; 77 for (int k = 0; k < bucketElementCounts.length; k++) { 78 // 如果桶中有数据 才放入到原数组 79 if (bucketElementCounts[k] != 0) { 80 // 循环该桶 即第K个桶 放入 81 for (int l = 0; l < bucketElementCounts[k]; l++) { 82 arr[index] = bucket[k][l]; 83 index++; 84 } 85 } 86 bucketElementCounts[k] = 0; 87 } 88 // [3, 14, 58, 214, 542, 748] 89 System.out.println("第三轮结果" + Arrays.toString(arr)); 90 }
5 通过循环实现基数排序(桶排序)
1 public static void main(String[] args) { 2 int[] arr = { 58, 3, 542, 748, 14, 214 }; 3 radixSort2(arr); 4 } 5 public static void radixSort2(int[] arr) { 6 // 1 得到数组中最大的数的位数 7 int max = arr[0];// 假设第一位就是最大数 8 for (int i = 1; i < arr.length-1; i++) { 9 if (arr[i] > max) { 10 max = arr[i]; 11 } 12 } 13 // 2 得到最大数是几位数 14 int maxLength = (max + "").length(); 15 16 int[][] bucket = new int[10][arr.length]; 17 int[] bucketElementCounts = new int[10]; 18 19 for (int i = 0,n = 1; i < maxLength; i++,n *= 10) { 20 for (int j = 0; j < arr.length; j++) { 21 // 取出每个元素的个位的值 22 int digitOfElement = arr[j] / n % 10; 23 bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j]; 24 bucketElementCounts[digitOfElement]++; 25 } 26 27 // 按照这个桶的顺序(一位数组的下标 取出数据,放入原理的数据) 28 int index = 0; 29 for (int k = 0; k < bucketElementCounts.length; k++) { 30 // 如果桶中有数据 才放入到原数组 31 if (bucketElementCounts[k] != 0) { 32 // 循环该桶 即第K个桶 放入 33 for (int l = 0; l < bucketElementCounts[k]; l++) { 34 arr[index] = bucket[k][l]; 35 index++; 36 } 37 } 38 // 第1轮处理后,需要将每个bucketElementCounts[k] = 0 清零 39 bucketElementCounts[k] = 0; 40 } 41 //System.out.println("第" + i + "次排序结果为" + Arrays.toString(arr)); 42 } 43 }
6 时间复杂度

7 时间复杂度测试
// 基数(桶)排序 public static void main(String[] args) { speedTest(80000); } /** * 创建一个随机数组 然后调用排序方法 得到时间 * * @param number 创建的随机数组个数 */ public static void speedTest(int number) { int[] arr = new int[number]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 800000); } SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); Date date1 = new Date(); String time1 = simpleDateFormat.format(date1); System.out.println("排序前的时间为:" + time1); // 调用上面的基数排序方法 radixSort2(arr); Date date2 = new Date(); String time2 = simpleDateFormat.format(date2); System.out.println("排序后的时间为:" + time2); }
时间复杂度测试结果
8万个数据测试结果大约不需要1秒
80万个数据测试结果大约不需要1秒
800万个数据测试结果大约不需要1秒
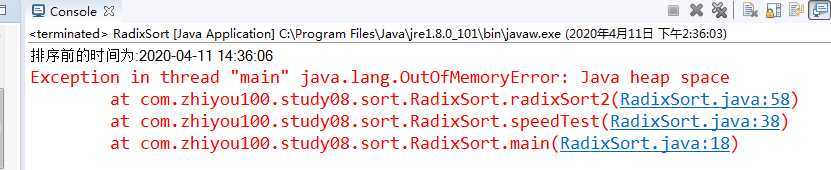
8000万个数据测试结果会超出虚拟机内存 因为基数排序是典型的拿空间换时间的排序
原文:https://www.cnblogs.com/wangxiucai/p/12679555.html