1.SOGI简介
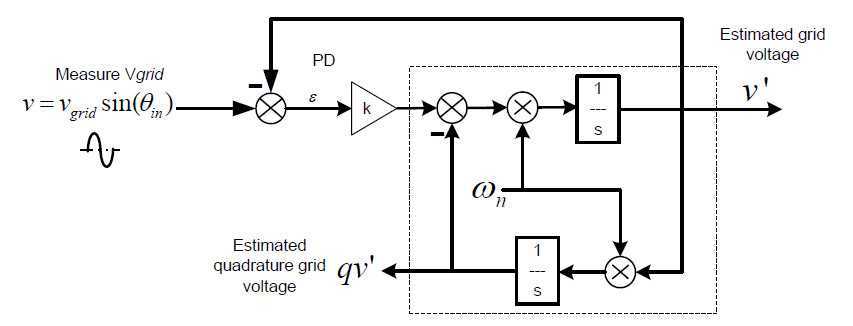
以TI官方文档中单相锁相环中SOGI应用为例
框图如下所示
正弦信号经过SOGI可得到同相信号及正交信号
2.传递函数
同相传递函数 网站Markdown用$$前后替代`
\[H_{d}(s)=\frac{v^{\prime}}{v}(s)=\frac{k \omega_{n} s}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{1}
\]
正交信号传递函数为
\[H_{d}(s)=\frac{v^{\prime}}{v}(s)=\frac{k \omega_{n} ^2}{s^{2}+k \omega_{n} s+\omega_{n}^{2}} \tag{2}
\]
3.离散化
采用双线性变换将s域函数离散至Z域
3.1 手动离散
双线性变换公式为
\[s=\frac{T_{s}}{2}\frac{z-1}{z+1} \tag{3}
\]
将式3代入式1得到
\[H_{d}(z)=\frac{k \omega_{n} \frac{T_{s}}{2}\frac{z-1}{z+1}}{(\frac{T_{s}}{2}\frac{z-1}{z+1})^{2}+k \omega_{n} (\frac{T_{s}}{2}\frac{z-1}{z+1})+\omega_{n}^{2}} \tag{4}
\]
这里使用以下两个替换
\[x=2k\omega_{n}T_{s} \tag{5}
\]
\[y=( \omega_{n} T_{s})^2 \tag{6}
\]
得到
\[H_{d}(z)=\frac{\left(\frac{x}{x+y+4}\right)+\left(\frac{-x}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{b_{0}+b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{7}
\]
同理得到正交函数的离散形式
\[H_{q}(z)=\frac{\left(\frac{k \cdot y}{x+y+4}\right)+2\left(\frac{k \cdot y}{x+y+4}\right) z^{-1}+\left(\frac{k \cdot y}{x+y+4}\right) z^{-2}}{1-\left(\frac{2(4-y)}{x+y+4}\right) z^{-1}-\left(\frac{x-y-4}{x+y+4}\right) z^{-2}}=\frac{q b_{0}+q b_{1} z^{-1}+q b_{2} z^{-2}}{1-a_{1} z^{-1}-a_{2} z^{-2}} \tag{8}
\]
连续函数离散化-以SOGI为例
原文:https://www.cnblogs.com/swear/p/12682551.html
